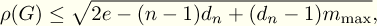
In addition, we give two upper bounds for l(G):
ACTA MATHEMATICA UNIVERSITATIS COMENIANAE
Abstract. Let G = (V,E) be a simple connected graph with n vertices and e edges. Assume that
the vertices are ordered such that d1 > d2 > ... > dn, where di is the degree of vi for
i = 1,2,...,n and the average of the degrees of the vertices adjacent to vi is denoted by
mi. Let mmax be the maximum of mi’s for i = 1,2,...,n. Also, let r
(G) denote the
largest eigenvalue of the adjacency matrix and l
(G) denote the largest eigenvalue of the
Laplacian matrix of a graph G. In this paper, we present a sharp upper bound on
r
(G):
In addition, we give two upper bounds for l(G):
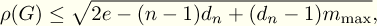
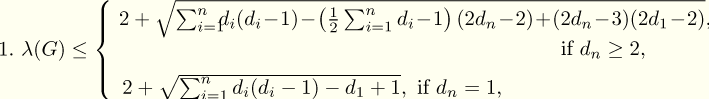
where the equality holds if and only if G is a regular bipartite graph or G is a star
graph, respectively.
2. l(G) < ![V~ -----[2e----n-2------------(----d--)]------
d1 + d21 + 4 n-1 + n-1d1 + (d1- dn) 1 - n1-1 mmax
-----------------------2-------------------------](da2x.gif) ,
,


© Copyright 2005, ACTA MATHEMATICA UNIVERSITATIS COMENIANAE