Cvičenie 1: ARIMA modely
:: ARMA modely - opakovanie z prednášky ::
- Definície procesov, podmienky stacionarity a invertovateľnosti
- ARMA modely sa používajú na modelovanie stacionárnych časových radov.
 je postupnosť nezávislých náhodných premenných s normálnym rozdelením, nulovou strednou hodnotou a disperziou
je postupnosť nezávislých náhodných premenných s normálnym rozdelením, nulovou strednou hodnotou a disperziou 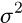 .
.
- AR(p) proces:
- AR = autoregresný proces (autoregressive)
- Proces:
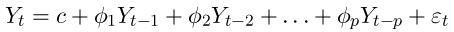
- Podmienka stacionarity: korene charakteristického polynómu sú mimo jednotkového kruhu.
- Podmienka invertovateľnosti: proces je vždy invertovateľný
- MA(q) proces:
- MA = proces kĺzavých priemerov (moving average)
- Proces:
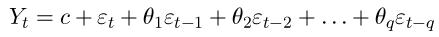
- Podmienka stacionarity: proces je vždy stacionárny.
- Podmienka invertovateľnosti: korene charakteristického polynómu sú mimo jednotkového kruhu.
- ARMA(p,q) proces:
- Proces:
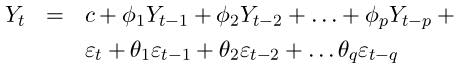
- Podmienka stacionarity: z AR časti procesu
- Podmienka invertovateľnosti: z MA časti procesu
- Proces:
- ARMA modely sa používajú na modelovanie stacionárnych časových radov.
- Autokorelačná (ACF) a parciálna autokorelačná funkcia (PACF) ARMA procesov
Alan Pankratz: Forecasting with Univariate Box - Jenkins Models. Concepts and Cases. John Wiley & Sons, Inc., 1983.
- Autokorelačná (ACF) a parciálna autokorelačná (PACF) funkcia ARMA procesov:
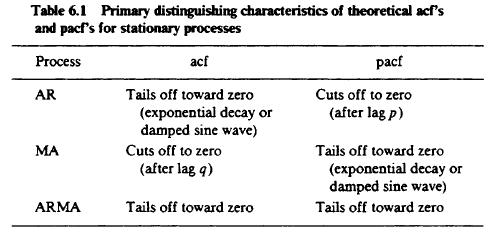
- Podrobnejšie pre procesy nižších rádov:

- AR(1) procesy:
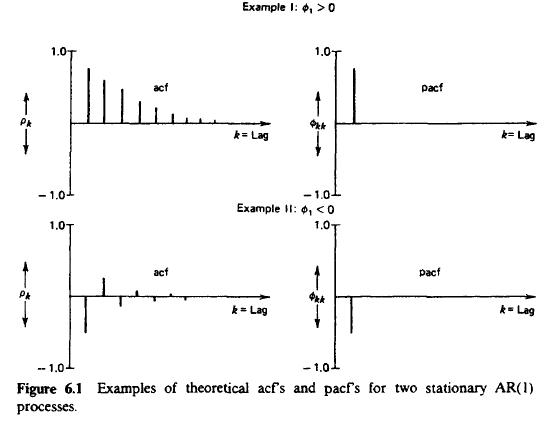
- AR(2) procesy:
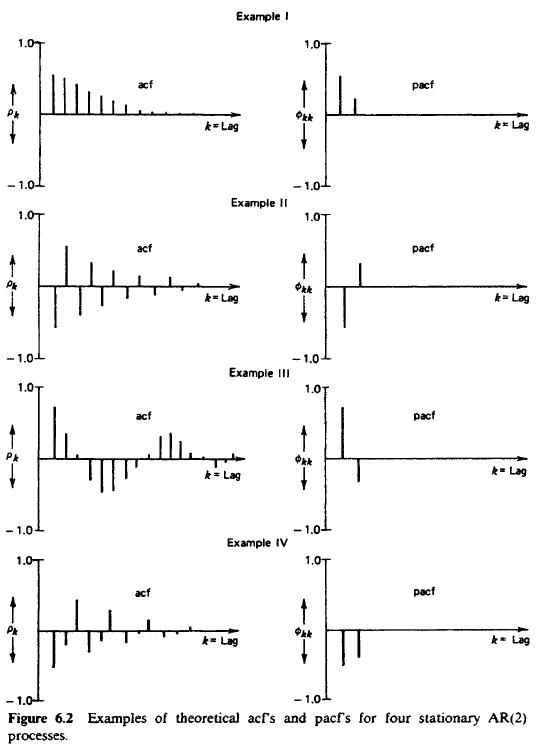
- MA(1) procesy:
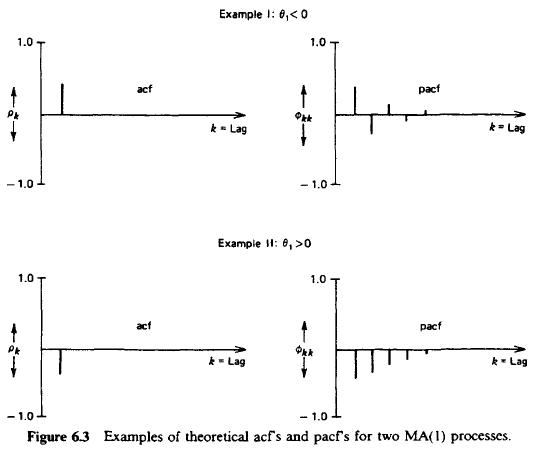
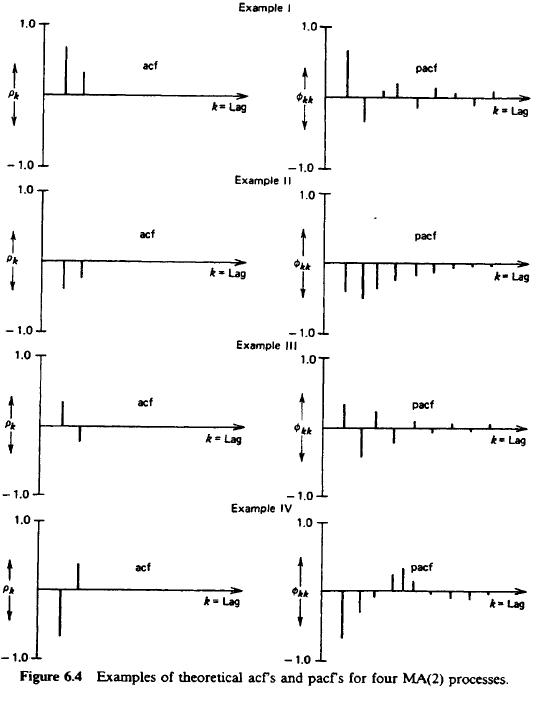
- MA(2) procesy:
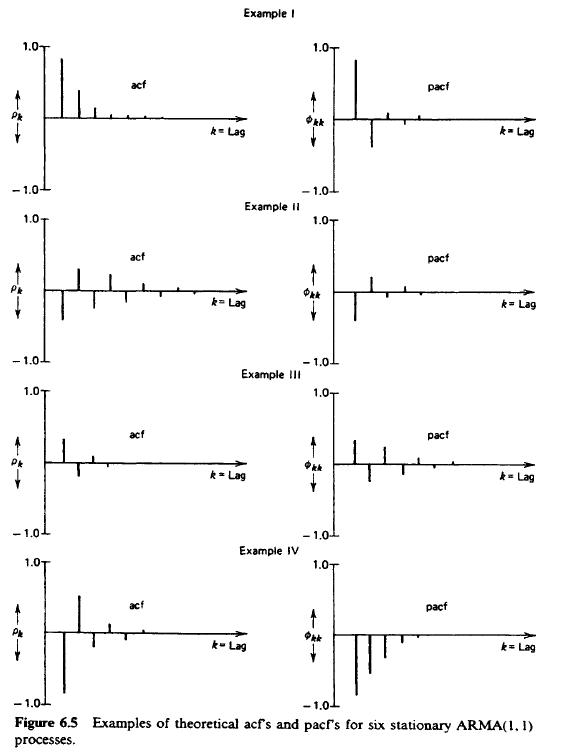
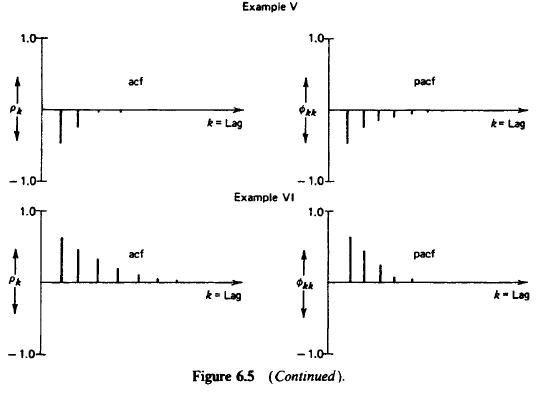
- ARMA(1,1) procesy:
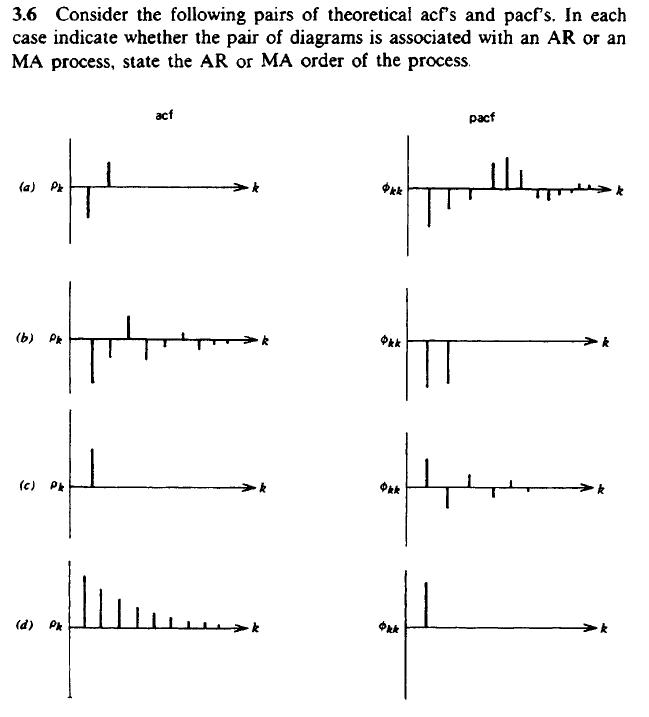
- Cvičenie: [Pankratz, exercise 3.6]
- Autokorelačná (ACF) a parciálna autokorelačná (PACF) funkcia ARMA procesov:
:: Príklad 1: Rozdiel dlhodobej a krátkodobej úrokovej miery ::
-
Dáta:
- Zdroj dát: http://www.lboro.ac.uk/departments/ec/cup/data.html (dáta k učebnici Mills, Markellos: The Econometric Modelling of Financial Time Series. Cambridge University Press, 2008.)
- Štvrťročné dáta, 1952Q1 - 2005Q4
- Premenné:
- Krátkodobá úroková miera: RSQ (91 day Treasury Bill rate)
- Dlhodobá úroková miera: R20Q (Yield on 20 Year UK Gilts)
- Workfile s dátami: [spread.wf1]
- Budeme modelovať premennú spread - rozdiel dlhodobej a krátkodobej úrokovej miery
-
Príprava dát:
-
Vytvoríme premennú spread:
a zobrazíme si jej priebeh:
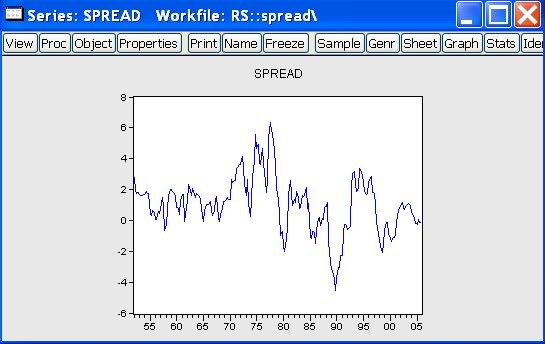
-
Vytvoríme premennú spread:
- Odhad autokorelačnej a parciálnej autokorelačnej funkcie
- Zobrazíme premennú (dvojkliknitím na jej názov vo workfile). Klikneme na Wiew - Correlogram
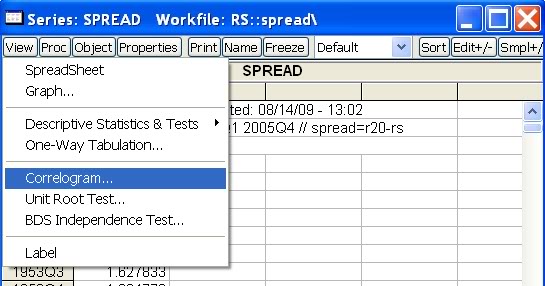
a potvrdíme, že chceme korelácie tejto premennej (nie diferencií):
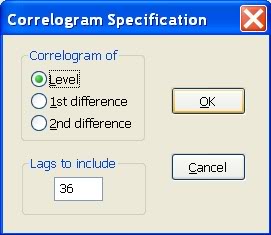
- Dostaneme výstup, ktorý obsahuje autokorelačnú a parciálnu autokorelačnú funkciu:
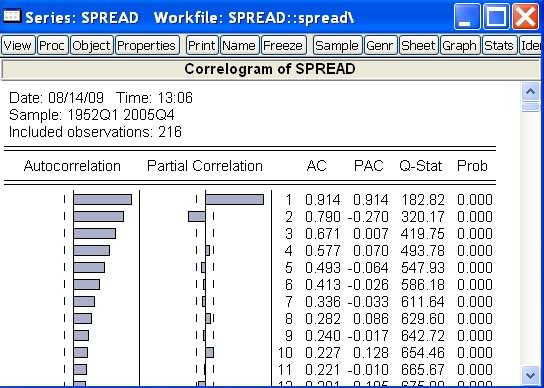
- Pozrime sa bližšie, čo všetko tento výstup obsahuje:
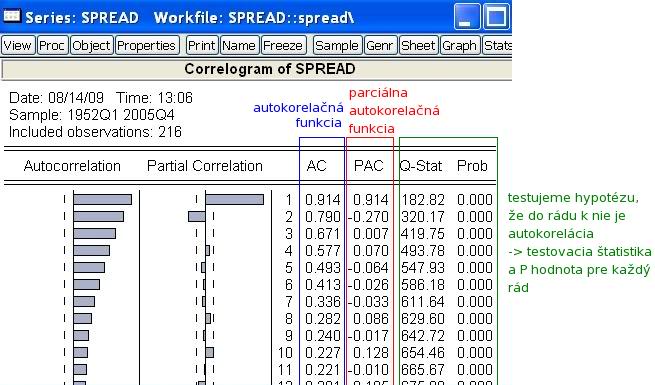
- Zobrazíme premennú (dvojkliknitím na jej názov vo workfile). Klikneme na Wiew - Correlogram
-
Výber modelu:
- Pozrieme sa na priebeh ACF a PACF:
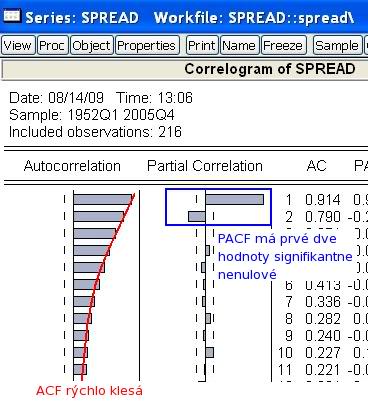
a porovnáme ich so známym priebehom teoretickej ACF a PACF procesov:
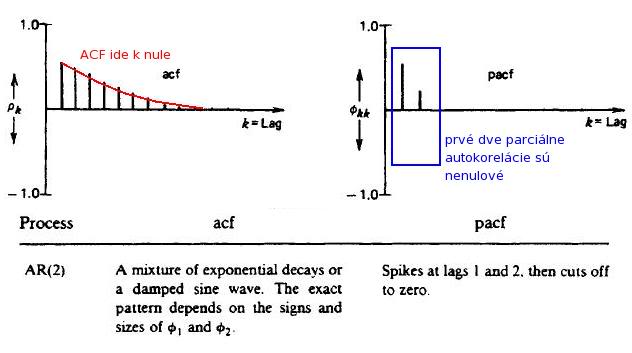
- V tomto prípade sa teda rozhodneme pre AR(2) model.
- Môže sa stať, že takýto jednoznačný záver nebudeme vedieť spraviť. Môžeme potom vyskúšať niekoľko modelov. Čo si treba na odhadnutom modeli všímať, ako zistiť, či je model vyhovujúci - tomu sa budeme venovať o chvíľu.
- Pozrieme sa na priebeh ACF a PACF:
-
Odhadnutie modelu v EViews:
- V menu klikneme na Quick - Estimate Equation.
- Zapíšeme modelovanú premennú, konštantu, AR členy (ar(1), ar(2), ... ar(p)) a MA členy (ma(1), ma(2), ... ma(q)). V tomto prípade odhadujeme AR(2) model, zapíšeme teda:
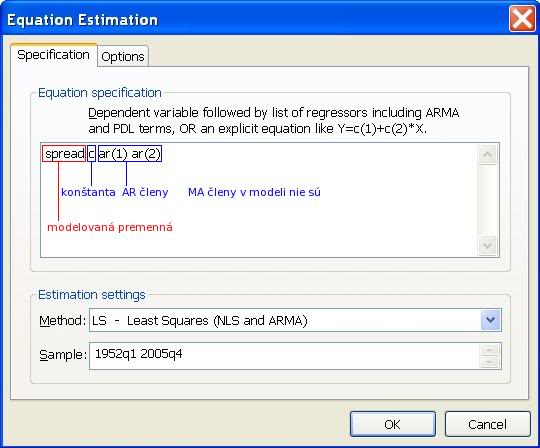
- Výstup, ktorý dostaneme:
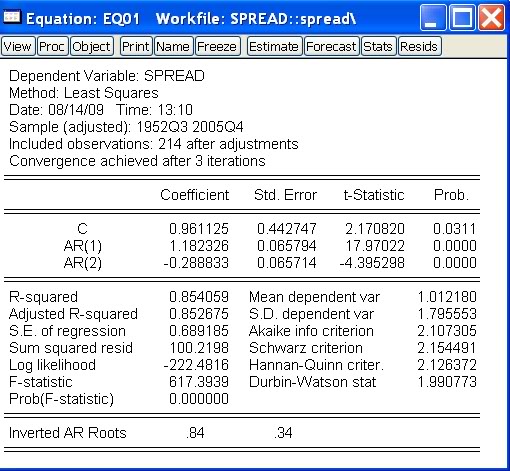
- V menu klikneme na Quick - Estimate Equation.
-
Overenie podmienok stacionarity a invertovateľnosti:
- Zopakujme si, čo budeme overovať:
- Podmienka staconarity - pre AR modely a pre ARMA modely (vychádza z AR časti modelu).
- Podmienka invertovateľnosti - pre MA modely a pre ARMA modely (vychádza z MA časti modelu)
- Obe podmienky overujeme pomocou príslušného polynómu - prevrátené hodnoty koreňov musia byť vnútri jednotkového kruhu.
- V tomto prípade máme AR proces, overujeme teda iba podmienku stacionarity. Korene sú priamo v okne s odhadnutým modelom:
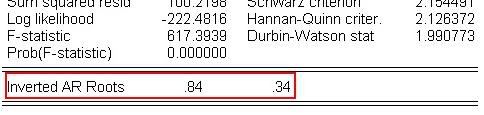
Vidíme, že ich absolútna hodnota je menšia ako 1, a teda podmienka stacionarity je splnená.
- Ak výjdu komplexné korene, je praktické pozrieť si priamo ich absolútne hodnoty (namiesto ich ručného výpočtu). V okne s odhadnutou rovnicou klikneme na View, kde vyberieme ARMA Structure:
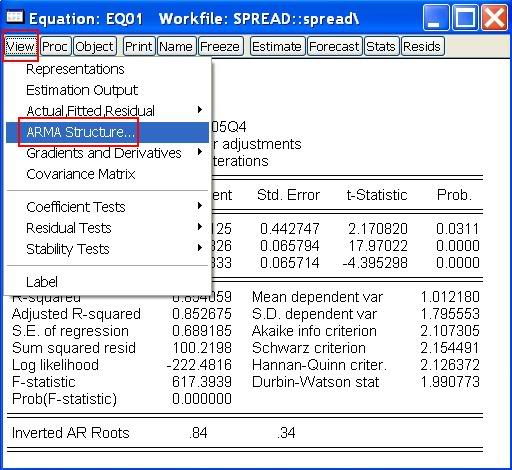
Zobrazí sa okno ARMA Diagnostic View, v ktorom zvolíme Roots a zobrazenie výsleku v tabuľke (Table):
Dostaneme:
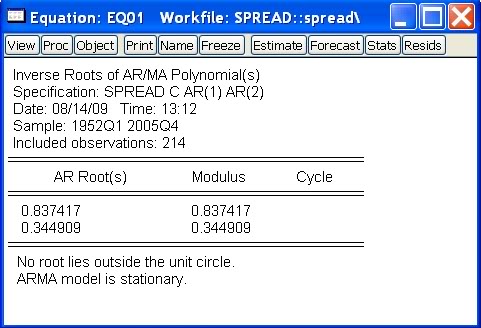
- Zopakujme si, čo budeme overovať:
-
Kontrola rezíduí
- Rezíduá musia byť bielym šumom, nemôže v nich zostať teda žiadna autokorelácia.
- Táto podmienka sa dá testovať viacerými spôsobmi, jedným z nich je Ljung-Boxova štatistika, ktorú sme už použivali. Pre časový rad rezídií budeme teda testovať hypotézu, že autokorelácia do rádu k je nulová. Ak sa hypotéza nezamieta, model je v poriadku.
- V okne s odhadnutou rovnicou klikneme na View a spomedzi Residual Tests vyberieme Correlogram - Q-Statistics:
Dostaneme:
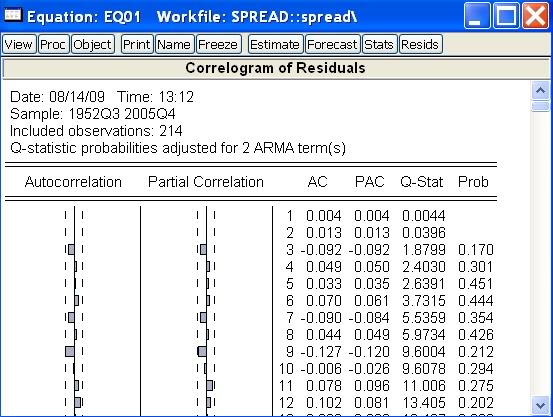
Model, ktorý sme zostavili, je teda aj na základe tohto testu vyhovujúci.
- Výpočet testovacej štatistiky je rovnaký ako predtým, keď sme počítali ACF pre zvolený časový rad. Ak ale časový rad predstavuje rezíduá, počet stupňov voľnosti závisí od toho, koľko ARMA členov obsahuje rovnica, z ktorej rezíduá vznikli. Preto je nevyhnutné, aby sme pracovali s oknom s rovnicou a testami z ponuky Residual Tests. Otvorením radu rezíduí a zobrazením jeho korelogramu by sme nedostali správne výsledky - pri výpočte P hodnôt by sa nezobrala do úvahy zmena počtu stupňov voľnosti.
- Rezíduá musia byť bielym šumom, nemôže v nich zostať teda žiadna autokorelácia.
-
Záver
- Na modelovanie rozdielu dlhodobej a krátkodobej úrokovej miery použijeme AR(2) model a na základe výstupu z EViews zapíšeme odhadnutú rovnicu, ktorou sa modelovaná premenná riadi (postup pre všeobecný ARMA model v nasledujúcom odstavci).
:: Zápis rovnice z výstupu EViews ::
-
Predpokladajme, že sme odhadli ARMA(2,2) model a dostali nasledovný výstup:
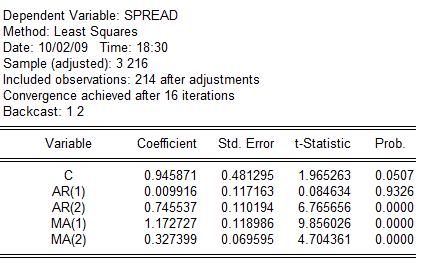
Rovnicu potom zapíšeme takto:

:: Príklad 2: Ceny kakaa ::
-
Dáta a model:
-
Ben Vogelvang: Econometrics. Theory and Applications with EViews. Pearson Education Limited, 2005.
Chapter 14.7. - The Box-Jenkins Approach in Practice - Mesačné dáta, január 1960 - september 2002.
- Dáta vo formáte xls: na stránke učebnice, súbor pcoccoftea.xls, zaujímajú nás hodnoty pcocoa; dáta načítané do workfilu: [pcocoa.wf1].
- Zopakujeme výpočty z učebnice:
- Budeme modelovať logaritmus ceny, zostavíme ARMA model pre diferencie tohto logaritmu.
- Odhadneme MA(1) a ARMA(1,2) modely.
- Potom model ARMA (1,2) odhadneme len s dátami z obdobia január 1960 - máj 2001. Pre zostávajúce mesiace spravíme predikciu pre log(pcocoa) a porovnáme ju so skutočným vývojom.
- Keďže budeme robiť predikcie pre log(pcocoa), odhadovaná rovnica musí obsahovať túto premennú. Vytvoríme teda novú premennú logpcocoa, modelovaná premenná (pri zápise do okna so špecifikáciou rovnice) bude D(logpcocoa).
-
Ben Vogelvang: Econometrics. Theory and Applications with EViews. Pearson Education Limited, 2005.
-
Poznámky:
- Modelovanie logaritmu premennej:
- V niektorých prípadoch môže zlogaritmovanie premennej viesť k stabilizovaniu variancie (podobne, ako v prípade lineárnej regresie, ktorú poznáte z ekonometrie). Modelovaniu variancie sa budeme venovať v nasledujúcich cvičeniach.
- Ak pracujeme s diferenciami časového radu, tieto sa dajú interpretovať ako relatívne zmeny (napr. relatívne zmeny ceny), výnosy (napr. výnosy akcií) a pod.
- Modelovanie diferencií premennej:
- Ak je potrebné spraviť diferencie na získanie stacionárneho časového radu, o pôvodnom rade sa hovorí, že je integrovaný.
- Neskôr sa budeme zaoberať štatistickými testami, podľa ktorých budeme schopní rozhodnúť, či môžeme s daným časovým radom pracovať, alebo ho treba zdiferencovať. Nateraz nám bude stačiť grafické "pravidlo" - na nestacionárny časový rad, ktorý treba zdiferencovať, nasvedčuje autokovariančná funkcia, ktorá klesá veľmi pomaly:
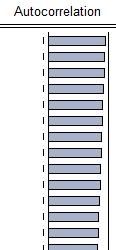
- Ak pre k-tu diferenciu (prvú, prípadne druhú alebo tretiu, vyššie sa prakticky nepoužívajú) vytvoríme ARMA(p,q) model, pre pôvodnú premennú sme vytvorili ARIMA(p,k,q) model.
- Modelovanie logaritmu premennej:
- Cvičenie: Odhadnite MA(1) a ARMA(1,2) modely, overte podmienky stacionarity a invertovateľnosti a testujte autokoreláciu rezíduí.
- Konštrukcia predikcií
- Ako sme povedali na začiatku, zoberieme model ARMA (1,2), ktorý je odhadnutý z dát z obdobia január 1960 - máj 2001:
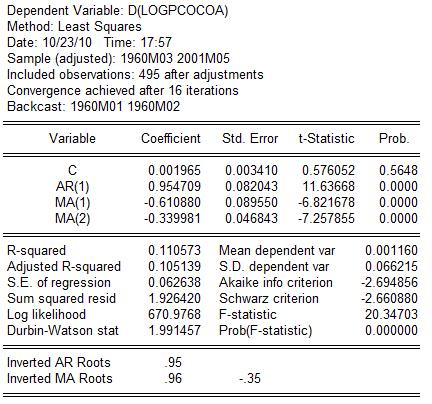
- V okne s odhadnutým modelom klikneme na Forecast:
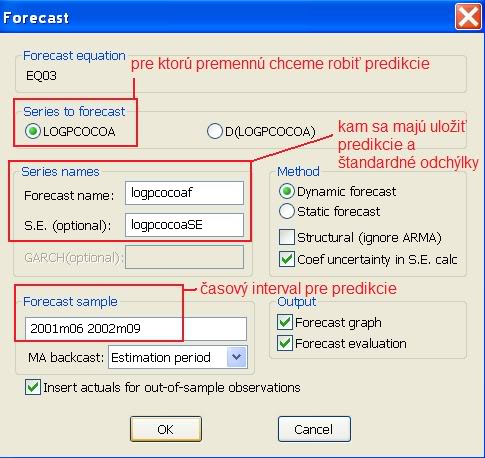
- Výstup: nasledovný graf (predikcie a intervaly spoľahlivosti, t.j. predikcia +/- 2*štandardná odchýlka) a premenné logpcocoaf, logpcocoaSE vo workfile
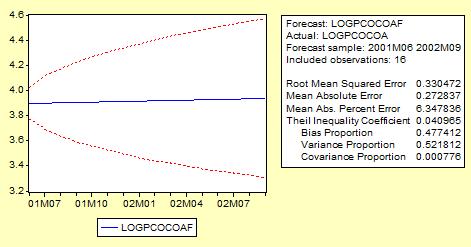
- Teraz môžeme porovnať predikcie so skutočnými hodnotami (zobrazením premenných logpcocoa, logpcocoaf, logpcocoaf-2*logpcocoaSE, logpcocoaf+2*logpcocoaf):
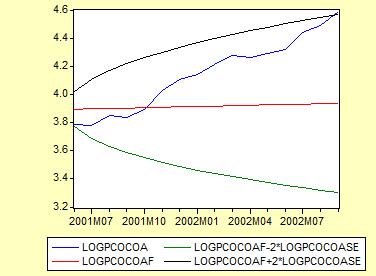
- Ako sme povedali na začiatku, zoberieme model ARMA (1,2), ktorý je odhadnutý z dát z obdobia január 1960 - máj 2001:
:: Cvičenia ::
-
Zo stránky http://www.stat.pitt.edu/stoffer/tsa2/ (stránka k učebnici R. H. Shumway, D. S. Stoffe: Time Series Analysis and Its Applications: With R Examples. Springer, 2006.) si stiahnite dáta cmort.dat
Súbor obsahuje denné dáta z rokov 1970-1979, vyjadrujúce úmrtnosť na kardiovaskulárne ochorenia v Los Angeles County.
Nájdite pre tieto dáta vhodný model.
- Vráťme sa k príkladu s cenou kakaa.
- Zostrojte predikcie pre MA(1) model.
- Ktorý z týchto dvoch modelov - MA(1), ARMA(1,2) - považujete za lepší? Odpoveď nie je jednoznačná, dôležitá je argumentácia a zohľadnenie rôznych kritérií.
- G. Kirchgässner, J. Wolters: Introduction to Modern Time Series Analysis. Springer, 2007.
Example 2.2:

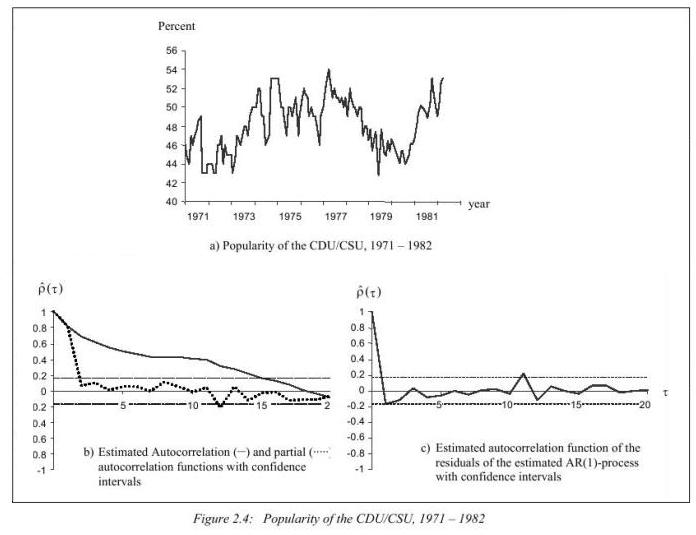
Zistite, či sa takýto model pre volebné preferencie vládnej strany dá použiť aj na Slovensku. Nájdite potrebné dáta a zistite, či je na ich modelovanie vhodný AR(1) proces. Ak áno, odhadnite model tak, že vynecháte nejaké dáta (napr. niekoľko mesiacov pred voľbami, niekoľko posledných mesiacov a pod.), spravíte predikcie a porovnáte ich so skutočnými hodnotami.
Čo ak na modelovanie a predikcie použijeme preferencie inej strany?
Cvičenia z časových radov, FMFI UK Bratislava, 2010.
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/
