Cvičenie 2: Jednotkový koreň, integrované procesy
- Na predchádzajúcom cvičení sme zostavovali model pre D(log(pcocoa)) s odôvodnením, že samotný logaritmus log(pcocoa) nie je stacionárny, ale diferencie stacionárne sú.
- Ako zistiť, že premennú treba diferencovať? Ako overiť, že diferencovanie viedlo k stacionárnemu časovému radu?
:: Jednotkové korene, integrované procesy, rád integrácie ::
- Korene charakteristického polynómu AR procesu musia byť v absolútnej hodnote menšie ako 1, jednotkový koreň spôsobuje nestacionaritu procesu. Ak je násobnosť jednotkového koreňa 1, tak prvé diferencie sú stacionárne. Ak je násobnosť jednotkového koreňa 2, tak druhé diferencie sú stacionárne. Rovnako pre vyššie násobnosti.
- Ak je násobnosť jednotkového koreňa k, tak k-te diferencie procesu sú stacionárne, hovoríme o integrovanom procese rádu k, ozn. I(k).
- Ako sa prejavuje I(k) proces:
- I(1) - lineárny trend, takýto charakter majú mnohé ekonomické premenné.
- I(2) - trend v rýchlosti rastu, napr. ceny a mzdy v niektorých obdobiach inflácie
- I(3) - napr. cenová úroveň počas hyperinflácie - medzivojnové Nemecko, Maďarsko po druhej svetovej vojne
- Pomôcka pri práci s dátami: typický pribeh autokorelačnej funkcie procesu s jednotkovým koreňom - korelácie klesajú veľmi pomaly:

- Postup:
- Testujeme pôvodný časový rad. Ak nemá jednotkový koreň, máme stacionárny časový rad koniec. Ak jednotkový koreň má, treba zistiť jeho násobnosť - krok 2.
- Testujeme prvé diferencie. Ak nemajú jednotkový koreň, násobnosť jednotkového koreňa v pôvodnom rade je 1. Je to I(1) proces, prvé diferencie sú stacionárne. - koniec. Ak aj prvé diferencie majú jednotkový koreň, násobnosť pôvodného koreňa je aspoň 2 - ideme na krok 3.
- Testujeme druhé diferencie. Ak nemajú jednotkový koreň, násobnosť jednotkového koreňa v pôvodnom rade je 2. Je to I(2) proces, druhé diferencie sú stacionárne. - koniec.
Vo výnimočných prípadoch (pozri interpretáciu v predchádzajúcej časti) má zmysel v prípade nezamietnutia jednotkového koreňa pre druhé diferencie ísť ďalej a testovať, či ide o I(3) proces.
Ako už bolo spomínané, integrované procesy vyšších rádov sa prakticky nepoužívajú.
:: ADF (augmented Dickey-Fuller) test ::
- Nulová hypotéza testu: časový rad má jednotkový koreň.
- Pracovať budeme s dátami z predchádzajúceho cvičenia o cenách kakaa ([pcocoa.wf1]), konkrétne s logaritmom ceny - s premennou log(pcocoa).
- V okne so zvolenou premennou klikneme na View - Unit Root Tests:
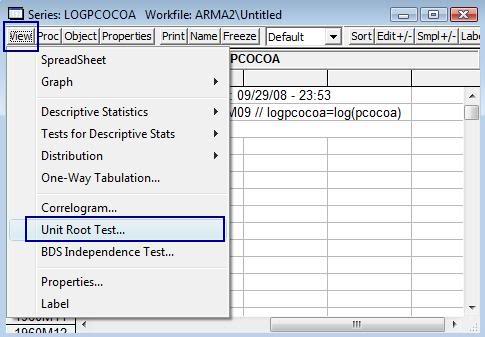
Zobrazí sa nám okno:
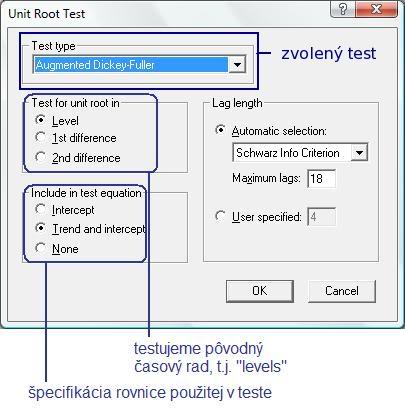
V časti Include in test equation sme zvolil najvšeobecnejšiu možnosť - Trend and intercept. Či sú oba tieto členy v rovnici potrebné, zistíme o chvíľu.
- Výstup:
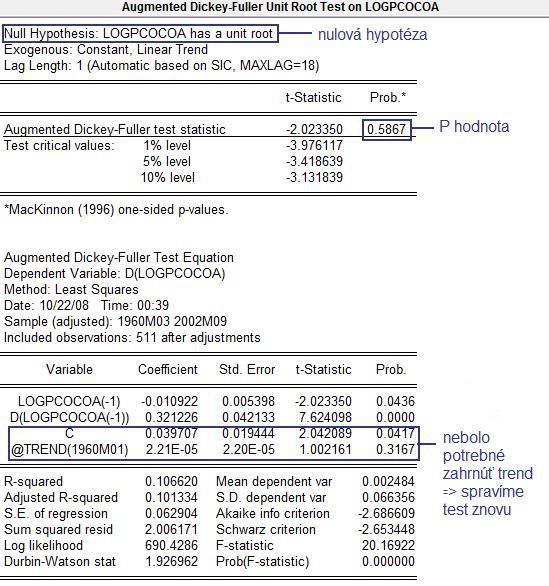
Dolu je pomocná regresia, na ktorej je založený ADF test. Pozrieme sa na premenn0 trend a intercept, ktoré sme do regresie zaradili. Vidíme, že trend nie je signifikantný, preto ADF test spravíme znovu, tentokrát ale v časti Include in test equation zvolíme možnosť Intercept
- V tejto novej pomocnej regresii sa aj intercept ukáže byť nesignifikantným. V okne so špecifikáciou testu v časti Include in test equation zvolíme None a dostaneme:
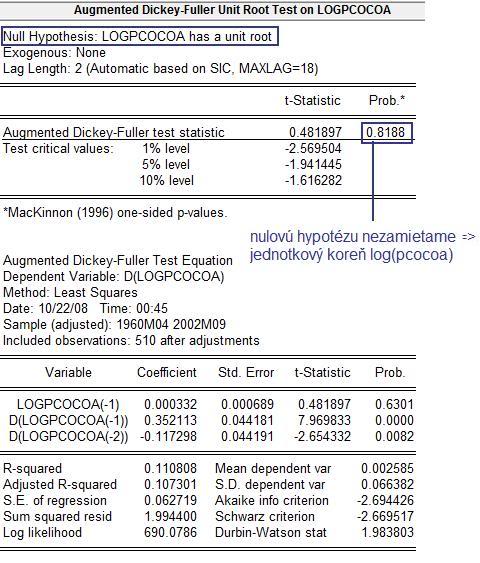
- Zisitili sme teda jednotkový koreň. Teraz treba zistiť jeho násobnosť. Testujeme teda prítomnosť jednotkového koreňa pre rad prvých diferencií, v časti Test for unit root in zvolíme 1st differences. Zistíme, že nie je potrebné zaradiť trend ani intercept a dostaneme:

Prvé diferencie už teda jednotkový koreň nemajú. Časový rad log(pcocoa) je teda I(1) - integrovaný proces prvého rádu. Prvé diferencie D(log(pcocoa)) sú stacionárne, a teda na ARMA modelovanie treba použiť tie. Pre pôvodnú premennú log(pcocoa) to znamená ARIMA(p,1,q) model.
:: Cvičenia ::
- Deflátor hrubého národného produktu
- Dáta v textovom súbore: [deflator.txt] - deflátor HDP, štvrťročné dáta, 1950-1983:
- Zdroj dát: http://pages.stern.nyu.edu/~wgreene/Text/econometricanalysis.htm - stránka učebnice W. Greene: Econometric Analysis. Prentice Hall, 2007.
- Pracovať budeme s logaritmami, t.j. s novou premennou log(deflator).
- Úlohy:
- Zistite rád integrácie daného časového radu. Akú premennú môžeme použiť na ARMA modelovanie?
- Zostavte pre premennú z predchádzajúcej otázky vhodný ARMA model. Aký model dostávame pre pôvodnú premennú? Napíšte odhadnutú rovnicu.
- Vynechajte niekoľko posledných rokov a odhadnite model bez nich. Spravte predikcie pre vynechané hodnoty a porovnajte ich so skutočnými.
- Hyperinflácia
- Hodnota bankoviek v Nemecku v r. 1923
- Dáta: [hyperinflacia.wf1] - cost of living (relatívne hodnoty, 1 = rok 1913), Nemecko, mesačné dáta od januára 1922 do júna 1923.
- Zdroj dát: http://www.business.uiuc.edu/lneal/hyperinflation1.htm
- Úlohy:
- Zobrazte priebeh dát.
- Na začiatku sme spomínali, že na modelovanie období hyperinflácie môže byť vhodný I(3) proces. Zistite, či sa takýto model dá použiť aj v tomto prípade (t. j. či treba dáta až trikrát diferencovať).
-
Trochu literatúry...
 Ako opisuje hyperinfláciu E. M. Remarque v románe Čierny obelisk:
Ako opisuje hyperinfláciu E. M. Remarque v románe Čierny obelisk:
- Hodnota bankoviek v Nemecku v r. 1923
- Parita kúpnej sily
- Testovanie stacionarity má aj iné aplikácie, ako je príprava dát na zostavenie ARMA modelu.
- Marno Verbeek: A Guide to Modern Econometrics, 2nd Edition. Wiley & Sons, 2004.
Chapter 8.5: Illustration: Long-run purchasing power parity (Part 1). - Parita kúpnej sily:
a jej súvislosť so stacionaritou časového radu:


- Dáta: purchasing power parity na stránke učebnice:
http://eu.wiley.com/legacy/wileychi/verbeek2ed/datasets.html
Zip archív obsahuje aj workfile s načítanými dátami.

- Použite tieto dáta na overenie PPP pomocou testovania stacionarity.
- Relatívne ceny
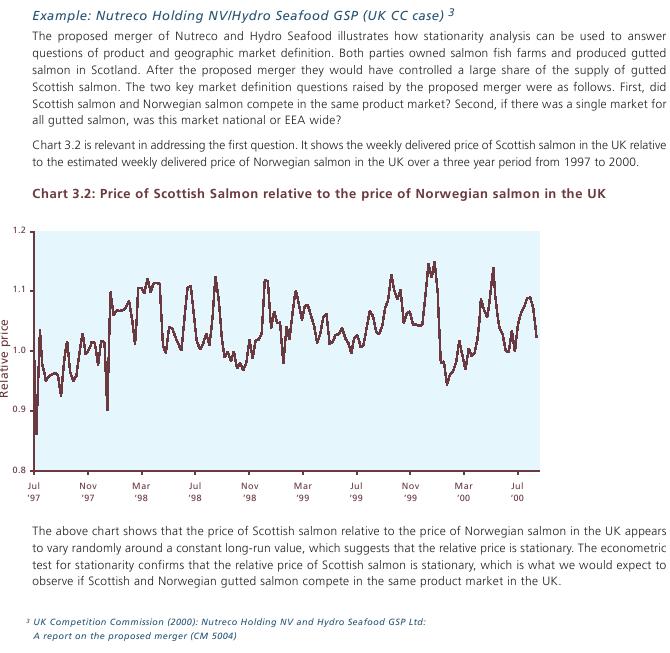
- Stacionarita relatívnej ceny:
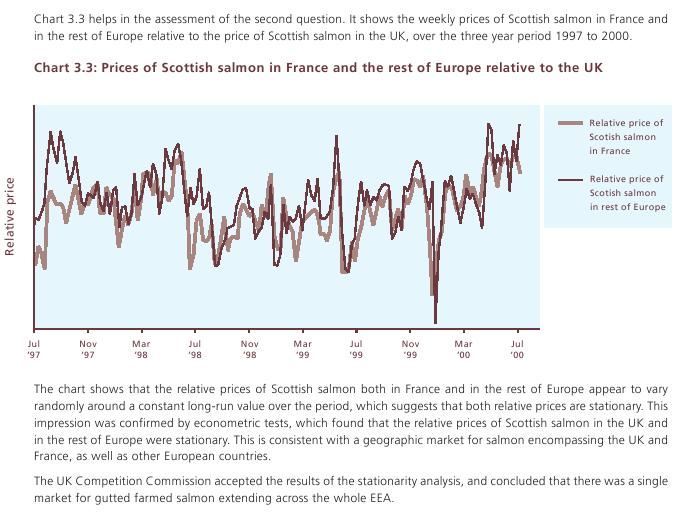
Zdroj: An Introduction to Quantitative Techniques in Competition Analysis. Lexecon Ltd. (http://www.lexecon.co.uk)
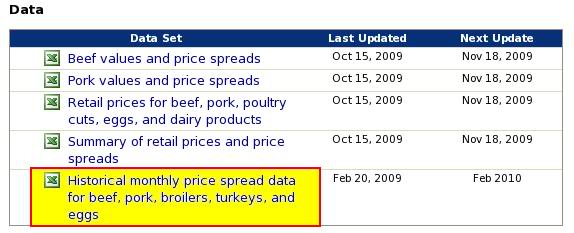
- Stiahnite si zo stránky http://www.ers.usda.gov/Data/MeatPriceSpreads/ historické dáta cien mäsa:
Vyberte z nich stĺpec retail value pre bravčové a hovädzie mäso:
 Testujte stacionaritu relatívnej ceny.
Testujte stacionaritu relatívnej ceny.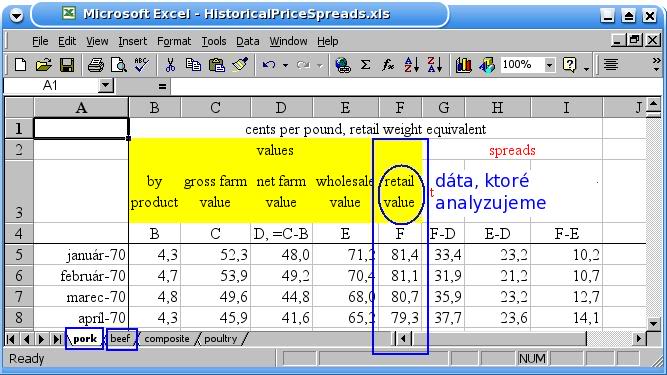
- Stacionarita relatívnej ceny:
Cvičenia z časových radov, FMFI UK Bratislava, 2010.
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/


