Cvičenie 3: Modelovanie volatility (ARCH, GARCH, ...)
:: ARCH a GARCH modely ::
- ARCH - autoregressive conditional heteroskedasticity - ide teda o modelovanie nekonštantnej disperzie
- GARCH - generalized ARCH
- Referencie na prvé články s týmito modelmi:
- ARCH model:
- Robert F. Engle, Autoregressive Conditional Heteroskedasticity With Estimates of the Variance of U.K. Inflation, Econometrica 50 (1982), pp. 987 - 1008.
- GARCH model:
- Tim Bollerslev, Generalized Autoregressive Conditional Heteroskedasticity, Journal of Econometrics 31 (1986), pp. 307 - 327
- Stephen J. Taylor, Modelling Financial Time Series, John Wiley, Chichester, 1986
- ARCH model:

:: Príklad: výnosy akcií ::
- Dáta: goog.txt, goog.wf1 - ceny akcií GOOG, týždenné dáta o začiatku r. 2007
- Vytvoríme vektor výnosov a zobrazíme ich priebeh:
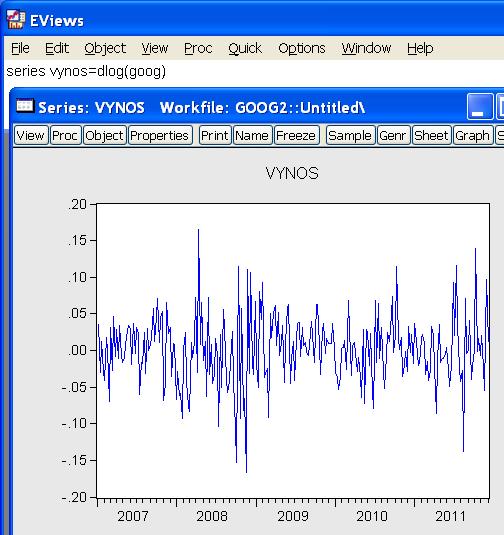
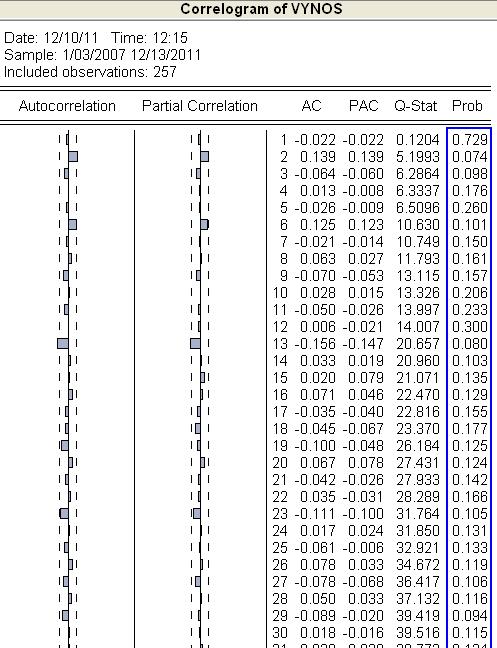
- Autokorelácie a parciálne autokorelácie nie sú signifikantné, Q štatistika sú tiež v poriadku. Zdá sa teda, že výnos je konštanta plus biely šum.
- Odhadneme tento model:
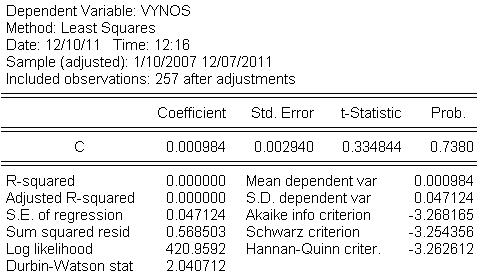
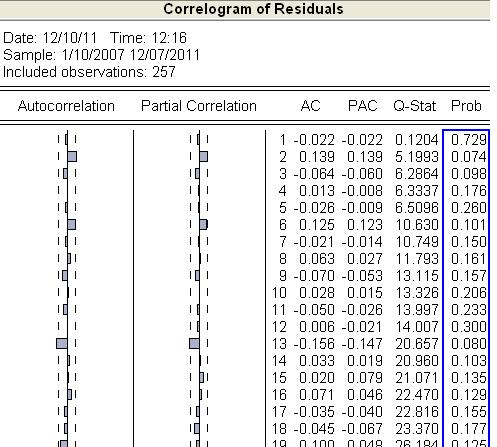
- ACF a PACF rezíduí sú rovnaké ako pre pôvodný časový rad, keďže sme od neho iba odrátali konštantu.
- Pozrime sa ale na priebeh rezídií:
Dostaneme:
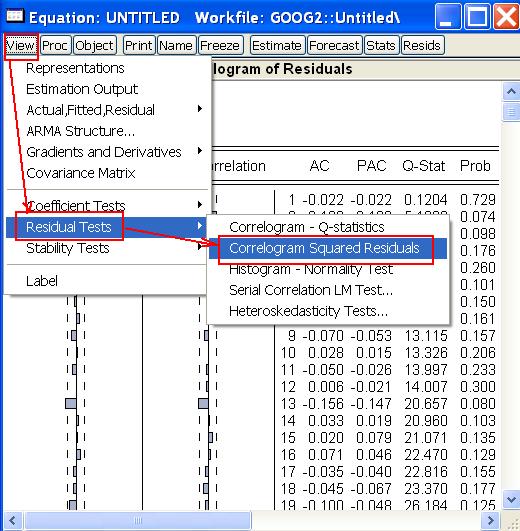 Ak by boli rezíduá bielym šumom, aj ich druhé mocniny by boli nekorelované. Toto nasvedčuje tomu, že nejde o biely šum, ale o proces s meniacou sa disperziou. Na prednáške sme si ukázali, že takýto priebeh sa dá modelovať ARCH a ARCH modelmi.
Ak by boli rezíduá bielym šumom, aj ich druhé mocniny by boli nekorelované. Toto nasvedčuje tomu, že nejde o biely šum, ale o proces s meniacou sa disperziou. Na prednáške sme si ukázali, že takýto priebeh sa dá modelovať ARCH a ARCH modelmi.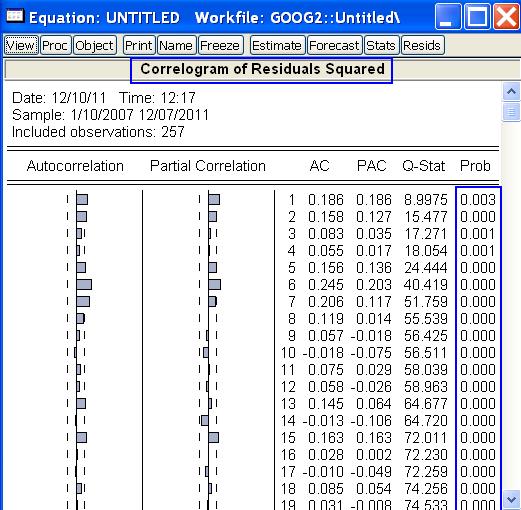
:: Definícia modelov a ich odhadovanie ::
- Opakovanie z prednášky:


- Odhadovanie (G)ARCH modelov v EViews:
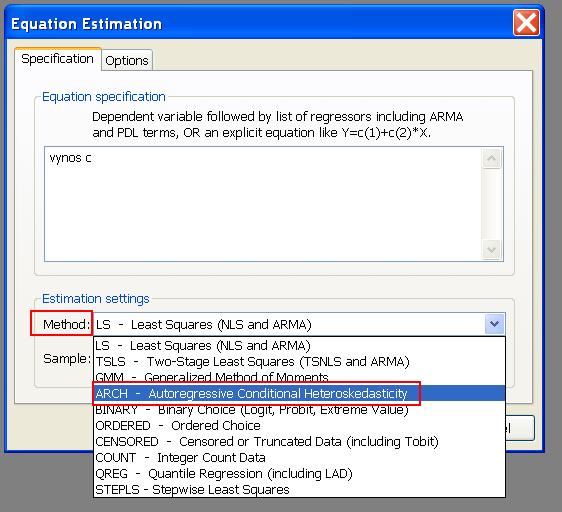
- Začneme rovnako ako doteraz - Quick - Estimate Equation. Tu z možností v časti Methods vyberieme ARCH - Autoregressive Conditional Heteroskedasticity:
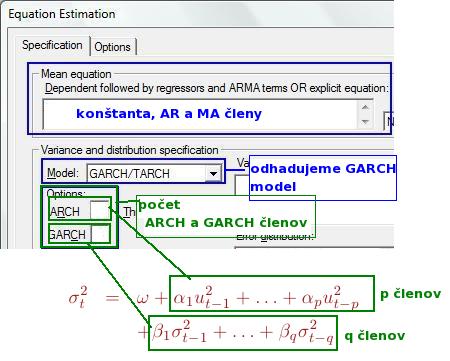
- Potom zadáme počet ARCH a GARCH členov:
- Začneme rovnako ako doteraz - Quick - Estimate Equation. Tu z možností v časti Methods vyberieme ARCH - Autoregressive Conditional Heteroskedasticity:
:: Príklad - pokračovanie ::
- Odhadneme ARCH(1):
- Ohraničenia na parametre sú splnené:
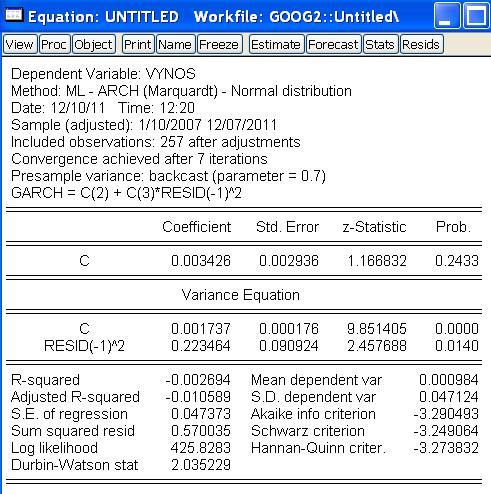
- Korelogram druhých mocnín rezíduí však nevyhovuje:
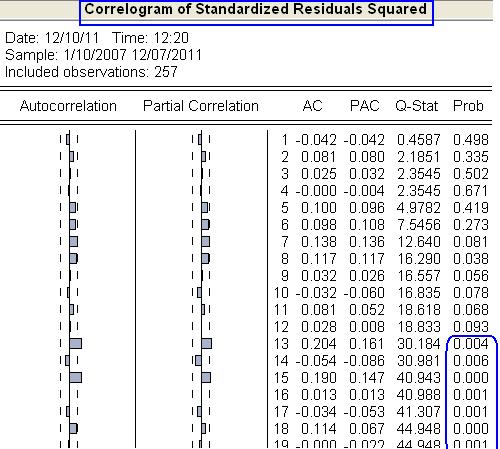
- Ohraničenia na parametre sú splnené:
- Podobne ak odhadneme ARCH(2):
- Ohraničenia na parametre sú splnené:
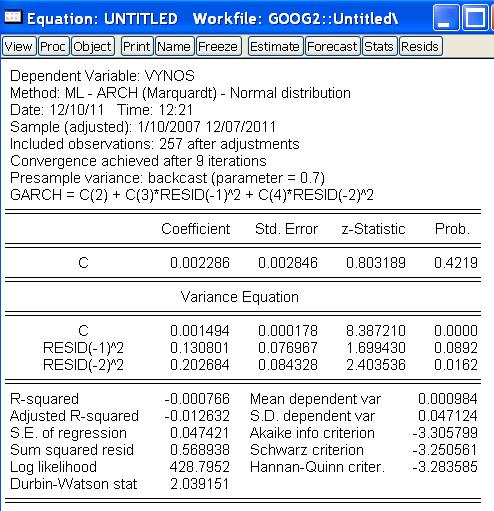
- Na základe korelogramu druhých mocnín rezíduí však model zamietneme:
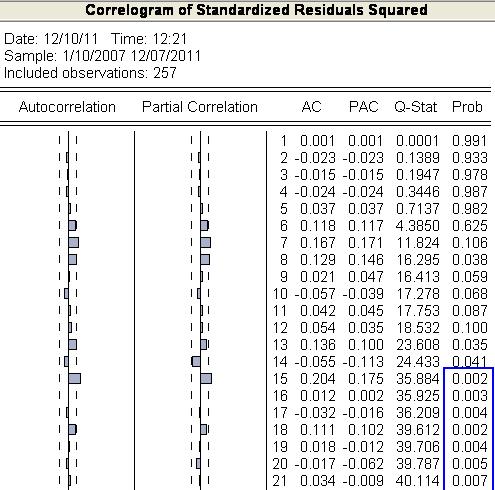
- Ohraničenia na parametre sú splnené:
- Pri procesoch vyššieho rádu už vznikajú problémy aj s podmienkami na parametre - výstup pre ARCH(4):

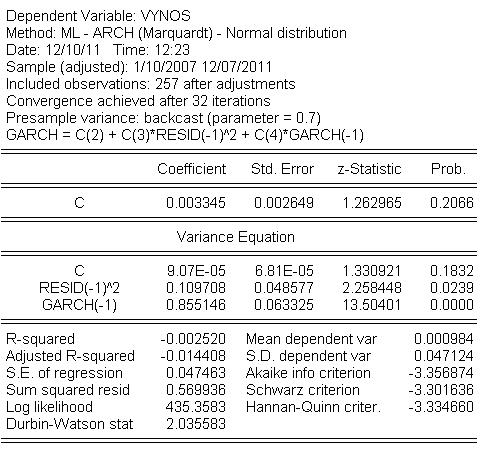
- Prejdeme na GARCH modely - odhadneme populárny GARCH(1,1):
- Ohraničenia na parametre sú splnené:
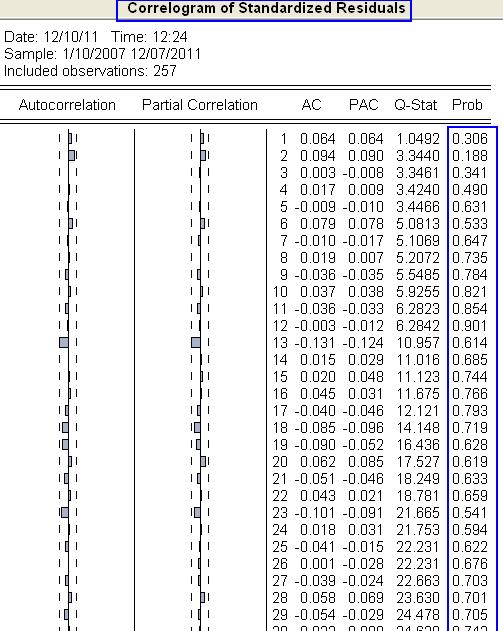
- Korelogram rezíduí je v poriadku:
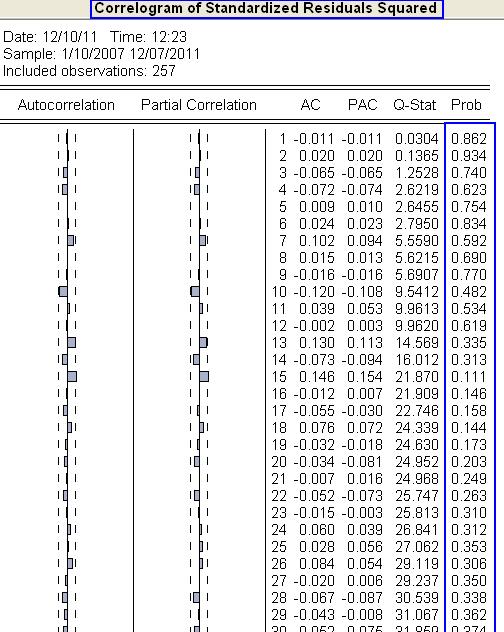
- Korelogram druhých mocnín rezíduí tiež:
- Ohraničenia na parametre sú splnené:
:: Odhadnutá disperzia ::
- Budeme pracovať s GARCH(1,1) modelom:
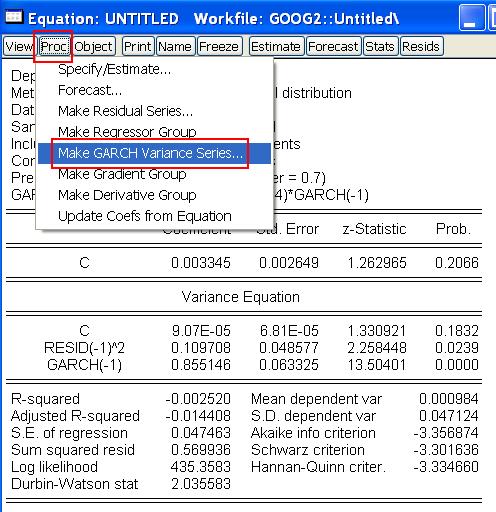
- V okne s odhadnutou rovnicou klikneme na Proc, odkiaľ vyberieme Make GARCH variance series
a zadáme názov premennej, do ktorej sa majú tieto variancie uložiť:
- Dostaneme:
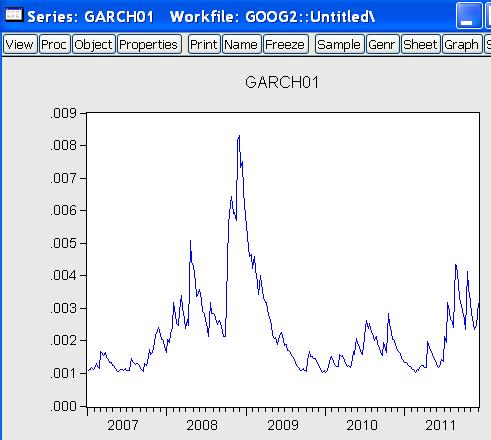
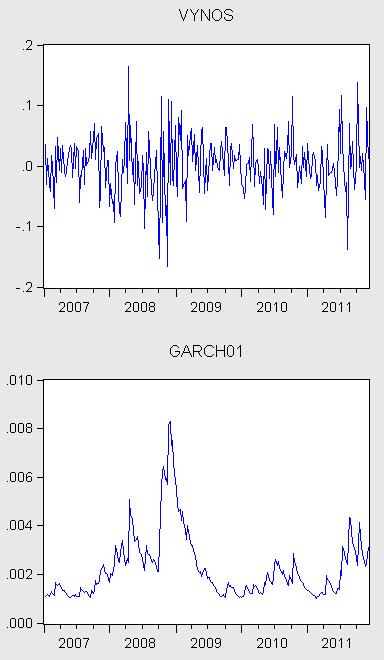
- Môžeme teraz porovnať priebeh tejto disperzie s vývojom výnosov - vidíme, ako sa zhodujú stabilné obdobia s malou odhadnutou varianciou a nestabilné obdobia s veľkou.
Cvičenia z časových radov, FMFI UK Bratislava, 2010.
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/
