ARMA modely
:: Odhadnutie a testovanie modelu ::
-
Dáta:
- Zdroj dát: http://www.lboro.ac.uk/departments/ec/cup/data.html (dáta k učebnici Mills, Markellos: The Econometric Modelling of Financial Time Series. Cambridge University Press, 2008.)
- Štvrťročné dáta, 1952Q1 - 2005Q4
- Premenné:
- Krátkodobá úroková miera: RSQ (91 day Treasury Bill rate)
- Dlhodobá úroková miera: R20Q (Yield on 20 Year UK Gilts) Na uvedenej stránke učebnice si ich môžete stiahnuť v txt formáte.
- Workfile s dátami: [spread.wf1]
- Budeme modelovať premennú spread - rozdiel dlhodobej a krátkodobej úrokovej miery
-
Stacionarita, resp. jednotkový koreň:
- Už vieme, že spread nemá jednotkový koreň a preto ho nediferencujeme. Model teda hľadáme pre premennú spread (bez diferencovania).
- Odhad autokorelačnej a parciálnej autokorelačnej funkcie
- Zobrazíme premennú (dvojkliknitím na jej názov vo workfile). Klikneme na View - Correlogram
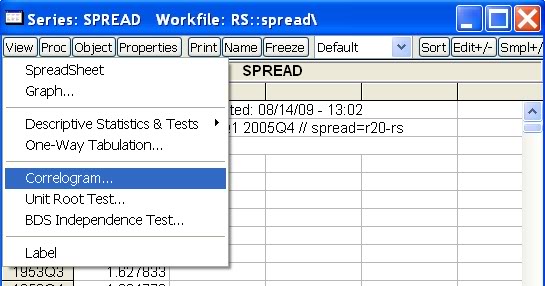
a potvrdíme, že chceme korelácie tejto premennej (nie diferencií):
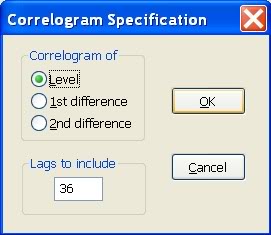
- Dostaneme výstup, ktorý obsahuje autokorelačnú a parciálnu autokorelačnú funkciu:
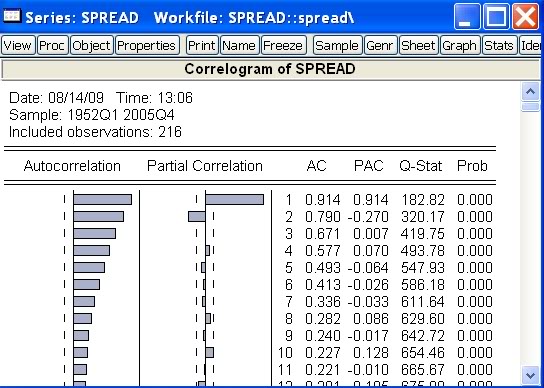
- Pozrime sa bližšie, čo všetko tento výstup obsahuje:
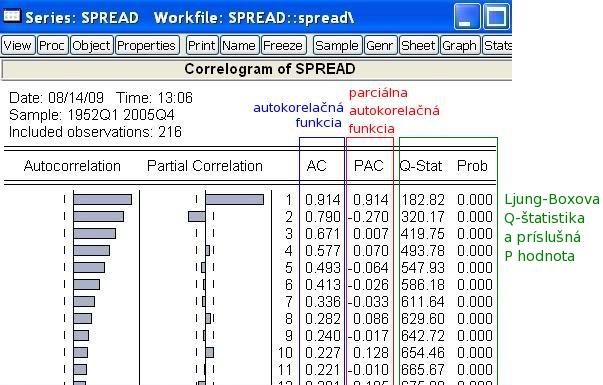
- Zobrazíme premennú (dvojkliknitím na jej názov vo workfile). Klikneme na View - Correlogram
-
Výber modelu:
- Pozrieme sa na priebeh ACF a PACF:
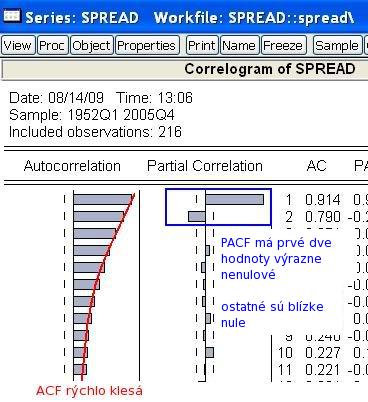
- Porovnáme ich so známym priebehom teoretickej ACF a PACF procesov. Na základe toho sa rozhodneme pre AR(2) model.
- Môže sa stať, že takýto jednoznačný záver nebudeme vedieť spraviť. Môžeme potom vyskúšať niekoľko modelov. Čo si treba na odhadnutom modeli všímať, ako zistiť, či je model vyhovujúci - tomu sa budeme venovať o chvíľu.
- Pozrieme sa na priebeh ACF a PACF:
-
Odhadnutie modelu v EViews:
- V menu klikneme na Quick - Estimate Equation.
- Zapíšeme modelovanú premennú, konštantu, AR členy (ar(1), ar(2), ... ar(p)) a MA členy (ma(1), ma(2), ... ma(q)). V tomto prípade odhadujeme AR(2) model, zapíšeme teda:
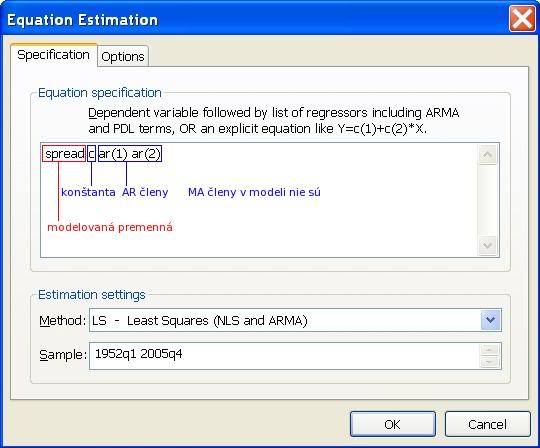
- Výstup, ktorý dostaneme:
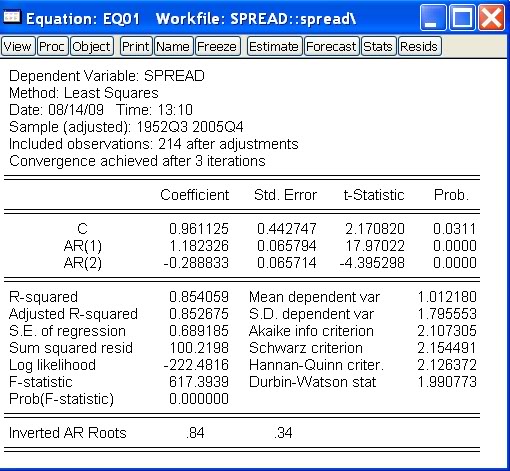
- V menu klikneme na Quick - Estimate Equation.
-
Overenie podmienok stacionarity a invertovateľnosti:
- Zopakujme si, čo budeme overovať:
- Podmienka staconarity - pre AR modely a pre ARMA modely (vychádza z AR časti modelu).
- Podmienka invertovateľnosti - pre MA modely a pre ARMA modely (vychádza z MA časti modelu)
- Obe podmienky overujeme pomocou príslušného polynómu - prevrátené hodnoty koreňov musia byť vnútri jednotkového kruhu.
- V tomto prípade máme AR proces, overujeme teda iba podmienku stacionarity. Korene sú priamo v okne s odhadnutým modelom:
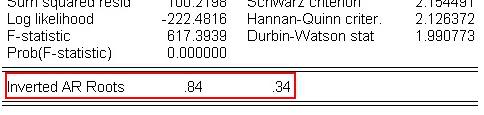
Vidíme, že ich absolútna hodnota je menšia ako 1, a teda podmienka stacionarity je splnená.
- Ak výjdu komplexné korene, je praktické pozrieť si priamo ich absolútne hodnoty (namiesto ich ručného výpočtu). V okne s odhadnutou rovnicou klikneme na View, kde vyberieme ARMA Structure:
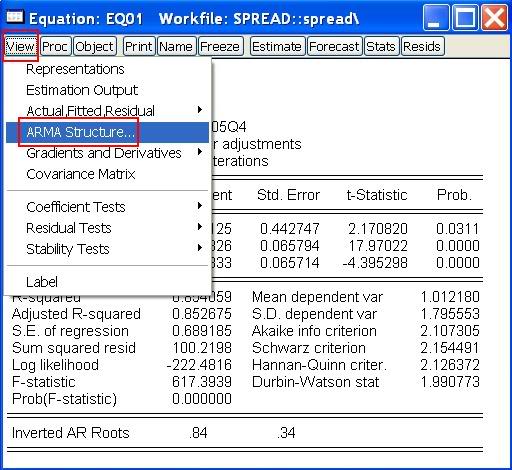
Zobrazí sa okno ARMA Diagnostic View, v ktorom zvolíme Roots a zobrazenie výsleku v tabuľke (Table):
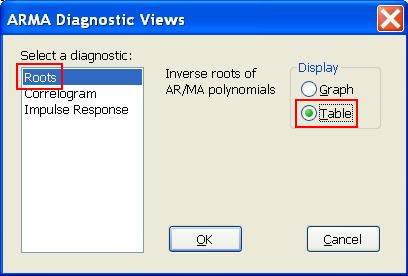
Dostaneme:
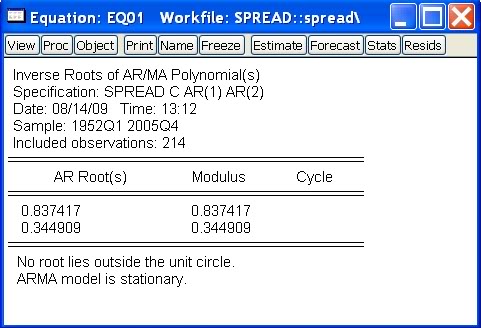
- Zopakujme si, čo budeme overovať:
-
Kontrola rezíduí
- Rezíduá musia byť bielym šumom, nemôže v nich zostať teda žiadna autokorelácia.
- V okne s odhadnutou rovnicou klikneme na View a spomedzi Residual Tests vyberieme Correlogram - Q-Statistics:
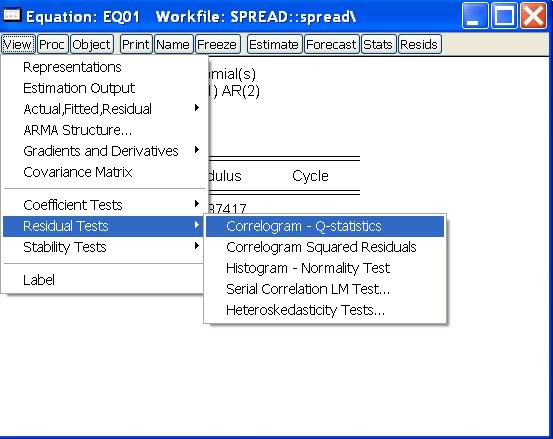
Dostaneme:
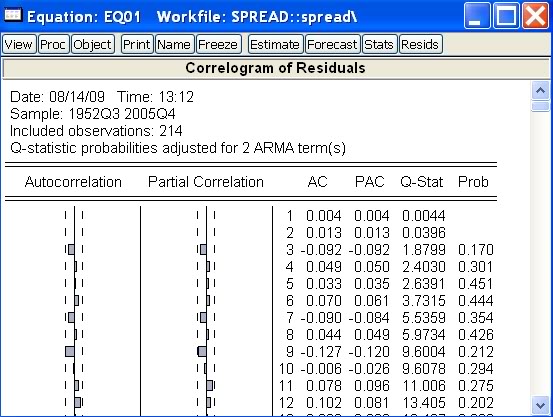
Pozrieme sa na intervaly spoľahlivosti, ako aj na Q-štatistiku. Model, ktorý sme zostavili, je aj na základe tohto testu vyhovujúci.
- Výpočet Q-štatistiky je rovnaký ako predtým, keď sme počítali ACF pre zvolený časový rad. Ak ale časový rad predstavuje rezíduá, počet stupňov voľnosti závisí od toho, koľko ARMA členov obsahuje rovnica, z ktorej rezíduá vznikli. Preto je nevyhnutné, aby sme pracovali s oknom s rovnicou a testami z ponuky Residual Tests. Otvorením radu rezíduí a zobrazením jeho korelogramu by sme nedostali správne výsledky - pri výpočte P hodnôt by sa nezobrala do úvahy zmena počtu stupňov voľnosti.
- Rezíduá musia byť bielym šumom, nemôže v nich zostať teda žiadna autokorelácia.
-
Záver
- Na modelovanie rozdielu dlhodobej a krátkodobej úrokovej miery použijeme AR(2) model a na základe výstupu z EViews zapíšeme odhadnutú rovnicu, ktorou sa modelovaná premenná riadi (postup pre všeobecný ARMA model v nasledujúcom odstavci).
:: Konštrukcia predikcií ::
- Dobrým spôsobom, ako otestovať model, je odhadnúť ho z menšieho počtu dát, spraviť predikcie a porovnať ich so skutočnými hodnotami.
- Odhadneme predchádzajúci model, pričom použijeme dáta iba do konca roku 2000. Zvyšné použijeme na porovnanie s hodnotami predikcií z tohto modelu.
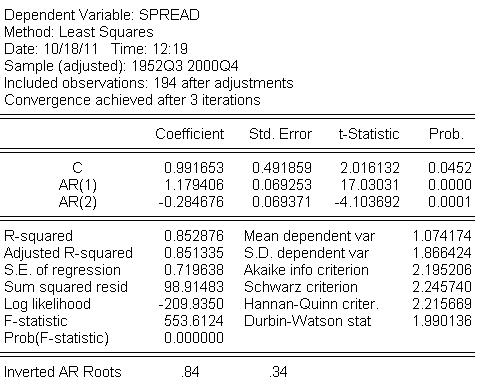
- Konštrukcia predikcií
- V okne s odhadnutou rovnicou klikneme na Forecast:
- Zapíšeme obdobie, pre ktoré chceme počítať predikcie a názvy premenných, do ktorých chceme uložiť tieto predikcie a ich štandardné odchýlky:
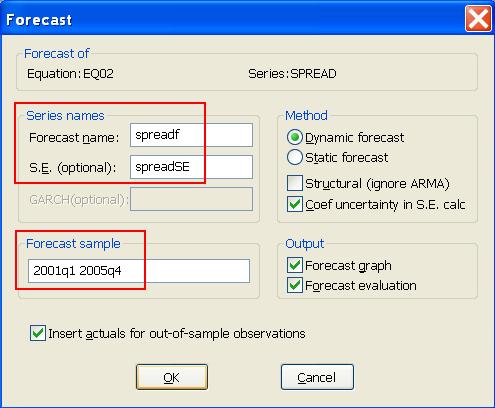
- Čo dostaneme - predikcie, intervaly spoľahlivosti, tabulľku:
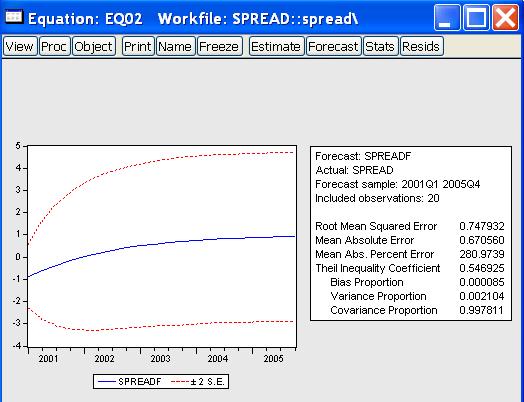
Čo vyjadrujú hodnoty v tabuľke:- Root Mean Squared Error, Mean Absolute Error, Mean Absolute Perc. Error - stredná kvadratická a absolútna chyba
- Theil Inequality Coefficient - číslo medzi nulou a jednotkou, nula znamená dokonalý fit
- Bias, Variance, Covariance proportion - v súčte dávajú jednotku. Prvé dve hodnoty hovoria o tom, ako sa priemer a variancia predikcií líšia od priemeru a variancie skutočných dát. Posledná hdonota meria zvyšnú, nesystematickú predikčnú chybu. Dobrý model by mal mať nízku hodnotu Bias a Variance proportion, väčšina predikčnej chyby by mala byť zahrnutá v Covariance proportion.
- Pomocou uložených hodnôt predikcií a štandarndných odchýlok môžeme nakresliť graf, v ktorom porovnáme predikcie a intervaly spoľahlivosti so skutočným vývojom:
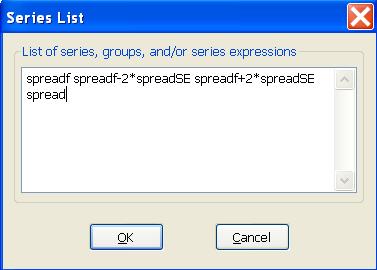
Dostaneme: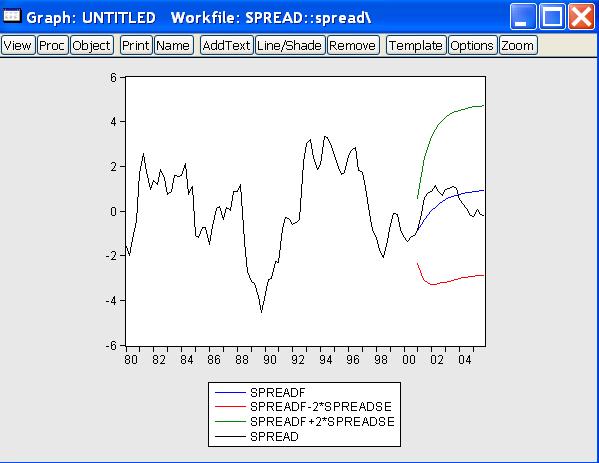
- V okne s odhadnutou rovnicou klikneme na Forecast:
:: Príklad na samostatné precvičenie ::
Odporúčam spraviť si ho predtým, ako začnete pracovať na domácej úlohe.-
Dáta a model:
-
Ben Vogelvang: Econometrics. Theory and Applications with EViews. Pearson Education Limited, 2005.
Chapter 14.7. - The Box-Jenkins Approach in Practice - Mesačné dáta, január 1960 - september 2002.
- Dáta vo formáte xls: na stránke učebnice, súbor pcoccoftea.xls, zaujímajú nás hodnoty pcocoa; dáta načítané do workfilu: [pcocoa.wf1]. Budeme pracovať s logaritmami týchto cien.
- Z prednásky: pre diferencie týchto dát je vhodný MA(1) model.
-
Ben Vogelvang: Econometrics. Theory and Applications with EViews. Pearson Education Limited, 2005.
- Úlohy:
- Zopakujete výpočty uvedené na prednáške:
- Zobrazte ACF pre logaritmy a ich diferencie.
- Odhadnite model MA(1), overte stacionaritu a invertovateľnosť, pozrite sa na autokoreláciu rezíduí.
- Odhadnite ARMA(2,1) model a porovnajte ich.
- Odhadnite model tak, že vynecháte nejaké posledné pozorovania (rok, pár rokov). Spravte predikcie pre logaritmus cien v tomto období a porovnajte ich so skutočnými hodnotami.
Poznámky- Keďže budeme robiť predikcie pre logaritmus ceny, odhadovaná rovnica musí obsahovať túto premennú. V zásade by sme mohli modelovanú premennú zapísať dvoma spôsobmi - ako D(log(pcocoa)) alebo D(logpcocoa), kde logpcocoa je nová premenná (vo workfile je už máme z testovania jednotkového koreňa ). Kvôli predikciám musíme použiť druhú možnosť.
- Pri predikciách potom vyznačíme, že chceme predikcie pre pôvodnú premennú, nie pre jej diferencie:
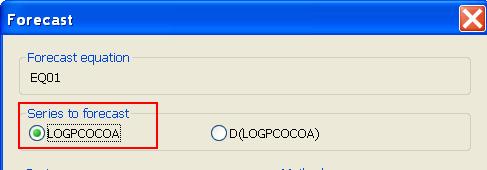
- Zopakujete výpočty uvedené na prednáške:
:: Zápis rovnice z výstupu EViews ::
-
Predpokladajme, že sme odhadli ARMA(2,2) model a dostali nasledovný výstup:
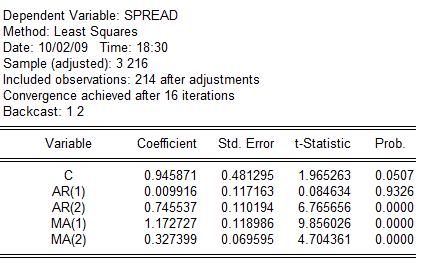
Rovnicu potom zapíšeme takto:

Časové rady, FMFI UK Bratislava, 2012.
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/
