Heteroskedasticita

Heteroskedasticita - disperzia náhodných chýb (epsilon) je je konštantná, porušenie predpokladu o konštantnosti disperzií.

Goldfeld-Quandtov test

Snow geeese
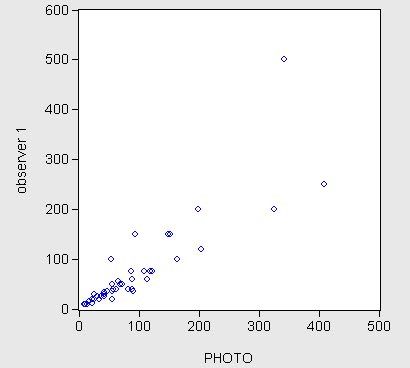
Aerial survey methods are regularly used to estimate the number of snow geese in their summer range areas west of Hudson Bay in Canada. To obtain estimates, small aircraft fly over the range and, when a flock of geese is spotted, an experienced person estimates the number of geese in the stock. To investigate the reliability of this method of counting, an experiment was conducted in which an airplane carrying two observers flew over n = 45 flocks, and each observer made an independent estimate of the of birds in each flock. Also, a photograph of the flock was taken so that an exact count of the number of birds in the flock could be made. The resulting data are in given in geese.txt.
As a result of this experiment, the practice of using visual counts of flock size to determite population estimates was discontinued in favor of using photographs.
S. Weisberg: Applied Linear Regression. John Wiley & Sons, 1985.
R. D. Cook, J. O. Jacobsen: Analysis of 1977 West Hudson Bay snow goose surveys. Unpublished report, Canadian Wildlife Services, 1977.
Model
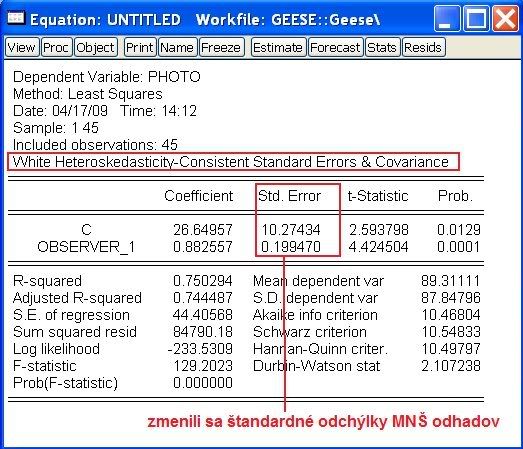
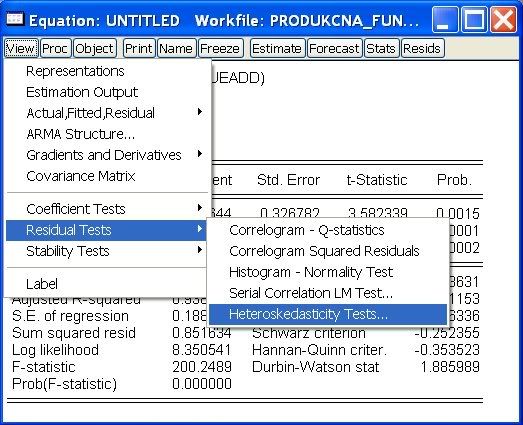
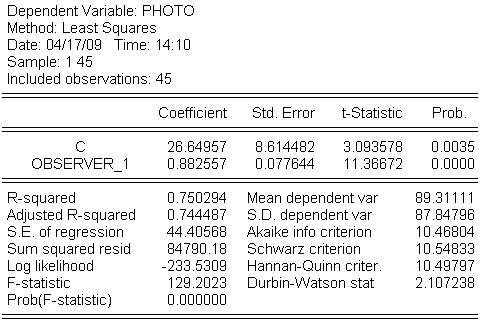
PHOTO = c(1) + c(2) OBS1 + ε,
kde PHOTO je skutočný počet husí (získaný z fotografie) a OBS1 je počet odhadnutý prvým pozorovatežom, najskôr odhadneme klasickým odhadom:

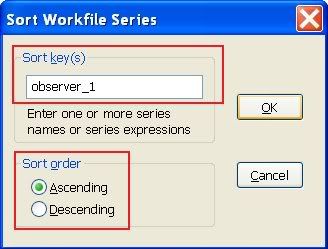
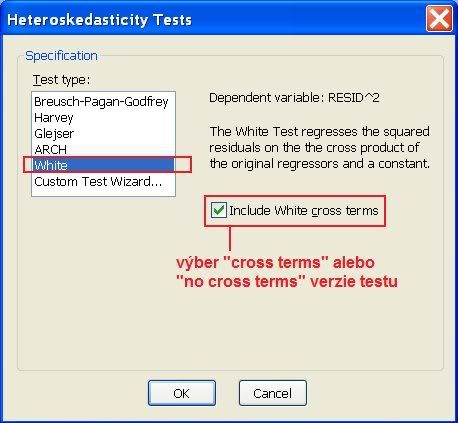
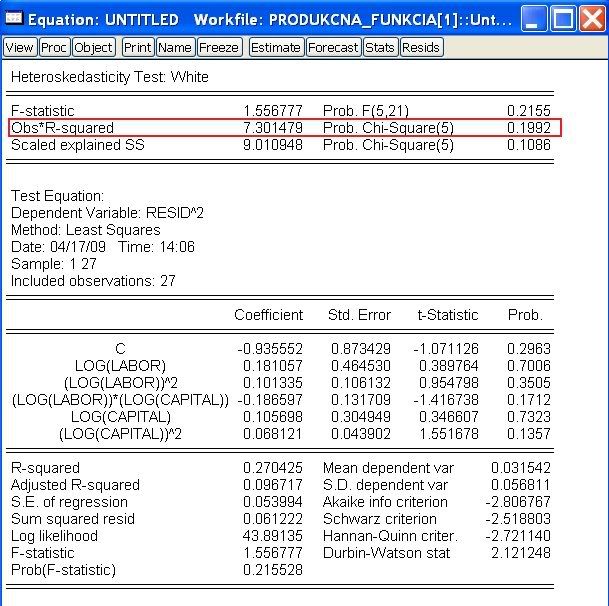
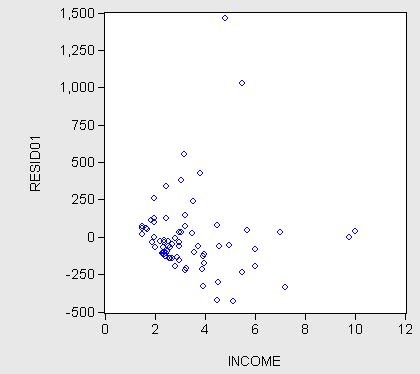
Máme však dôvod domnievať sa, že variancia chýb ε_i nie je konštantná. Ak náš odhad je, že v kŕdli je päť husí, je to zrejme presnejší odhad, ako keď ich počet odhadneme ako sto. To by znamenalo heteroskedasticitu v modeli.
Goldfeld-Quandtov test. Jeho použitie predpokladá, že máme premennú o ktorej si myslíme, že spôsobuje heteroskedasticitu - pre malé hodnoty tejto premennej je disperzia báhodných chýb malá, pre veľké hodnoty je disperzia veľká (alebo naopak).
Idea:. Zoradíme dáta podľa tejto premennej Prvá polovica takto zoradených dát bude tvoriť prvú skupinu dát v teste, druhá polovica dát bude tvoriť druhú skupinu. Teraz odhadneme dve regresie: regresiu z prvej skupiny dát (dáta s menšími hodnotami "podozrivej premennej") a regresiu z druhej skupiny dát (dáta s väčšími hodnotami). Inou možnosťou je rozdeliť dáta na tri skupiny a strednú vynechať. V kadom prípade dostávame dve skupiny dát. Ak je naše podozrenie správne, v jednej skupine je variancia väčšia. Nulová hypotéza testu je, že variancie v oboch skupinách sú rovnaké, čo zodpovedá homoskedasticite. Ak túto hypotézu zamietneme, znamená to heteroskedasticitu.
Testovacia štatistika. Odhadneme model v oboch skupiných dát a odhadneme aj disperziu náhodnej zložky. Testovacou štatistikou je podiel odhadov disperzií náhodných chýb, pričom v čitateli je väčšia hodnota. Rozdelenie za platnosti nulovej hypotézy je Fisherovo, stupne voľnosti sú n1-k, n2-k (n1 je počet dát v skupine, ktorej odhad je v čitateli; n2 počet dát v skupine, ktorá je v menovateli; k je počet parametrov modelu).
Usporiadanie dát v EViews:
Testujte v modeli heteroskedasticitu použitím Goldfeld-Quandtovho testu.

Odhadovanie modelu s heteroskedasticitou

Môžeme použiť MNŠ odhad, ale treba zmeniť výpočet štandardných odchýlok odhadov a teda aj testovanie signifikancie parametrov.
Všeobecný postup, ktorý nevyťaduje špecifikáciu formy heteroskedasticity - Whitov odhad kovariančnej matice.
Whitov odhad kovariančnej matice v Eviews: Pri odhadovaní rovnice klikneme na Options a zvolíme Whitov odhad:

Výsledok:

Testovanie hypotéz v modeli s heteroskedasticitou

F štatistiky sa nedajú použiť, namiesto nich sa používa Waldov test a chí kvadrát testovacia štatistika.
V Eviews: rovnaký postup ako predtým, ale všímame si chí kvadrát štatistiku (namiesto F) a príslušnú P hodnotu.
Testujte hypotézu, že odhad pozorovateľa je nevychýlený, t.j. skutočný počet husí je jeho odhad plus náhodná odchýlka (ktorá má nulovú strednú hodnotu).

Whitov test heteroskedasticity

Nie vždy máme k dispozícii jednu premennú, ktorá by mala heteroskedsticitu spôsobovať.
Existuje všeobecný test, ktorý takýto predpoklad nepotrebuje - Whitov test.
Idea: Druhé mocniny rezíuí modelujeme pomocou pôvodných regresorov a ich kombinácií. Ako kombinácie sa berú ich druhé mocniny (tzv. "no cross terms" verzia testu) alebo druhé mocniny a vzájomné súčiny (tzv. "cross terms"). Dobrý fit takejto regresie nasvedčuje tomu, že je v modeli heteroskedasticita. Nulová hypotéza je homoskedasticita.
Testovacia štatistika: počet dát krát koeficient determinácie v horeuvedenej pomocnej regresii. Za platnosti nulovej hypotézy má chí kvadrát rozdelenie, počet stupňov vožnosti je počet parametrov v pomocnej regresii okrem konštanty.
V EViews, príklad o produkčnej funkcii z predchádzajúceho cvičenia:

Výstup:
Použite tento test na dáta o odhadovaní počtu husí v kŕdli (obe jeho verzie).

Ako nájsť premennú, ktorá spôsobuje heteroskedasticitu

Whitov test môže mať malú silu, nemusí heteroskedasticitu odhadliť. Ak nám teda povie, že v modeli heteroskedasticita nie je, mali by sme sa pozrieť na model znovu a nájsť konkrétnejšiu hypotézu o tom, ako by heteroskedasticita mohla vyzerať a otestovať ju.
Ak sa podža Whitovho testu v modeli nachádza heteroskedasticita, je zaujímavé zistiť, čo ju spôsobuje. Tento výsledok je možné ďalej použiť pri modelovaní.
Ako teda nájsť premennú, ktorá by mohla vstupovať do Goldfeld-Quandtovho testu?
Užitočné je nakresliť si scatter plot, ktorý má na x-ovej osi hodnoty vysvetžujúcej premennej a na y-ovej rezíduá. Ak rozptyl rezíduí nie je konštatntný, je to príznakom heteroskedasticity.
Príklad: Budeme pracovať s dátami zo stránky učebnice Greene: Econometric Analysis - časť Data Tables, tabuľka Table F8.1:

Budeme uvažovať len tie pozorovania, pre ktoré sú výdavky z kreditných kariet nenulové

a z nich odhadneme model, v ktorom budeme modelovať výdavky z kreditných kariet pomocou veku, príjmu a jeho druhej mocniny a pomocou dummy premennej OWNRENT.
Testujte heteroskadasticitu najskôr Whitovym testom.
Model dáva určitú teoretickú hodnotu výdavkov (čo očakávame u daného človeka na základe jeho charakteristík). Dá sa však očakávať, že príjem bude mať vyplyv na disperziu odchýlok od tejto teoretickej hodnoty - čím väčší príjem, tým väčšia dispezia (väčší priestor pre rôzne správanie, čo sa týka platieb kreditnou kartou).

Testujte teraz heteroskadasticitu Goldfeld-Quandtovym testom.
Poznámka: V EViews sa vo workfile ukladajú rezíduá z poslednej regresie, prepisuje sa vektor resid. Je vak moné vytvoriť vektor rezíduí z regresie, ktorý sa nebude prepisovať a je s ním možné kedykožvek pracovať:

Čo ak máme viac premenných, o ktorých si myslíme, že spôsobujú heteroskedasticitu?

Nie vždy sa dá určiť jedina spomedzi premenných, ktorá by mala ovplyvňovať dispeziu náhodných chýb. Viac premenných môže vplývať súčasne.
V tomto prípade sa dajú použiť ďalšie testy, ktoré ponúka EViews: Breusch-Pagan-Godfrey, Harvey, Glejster.
Zistite v helpe, ako tieto testy fungujú a použite ich na zvolený model.

Ďalšie úlohy

Vo všetkých prípadoch pouťite najskôr Whitov test (obe verzie).
Potom si zostrojte grafy (premenná-rezíduá, pre všetky premenné) a skomentujte ich.
Zvožte si ďalší test, podľa toho, či chcete testovať vplyv jednej premennej alebo viacerých. Zdôvodnite (predchádzajúca grafická analýza, logická interpretácia).
Ak v niektorom teste zistíte heteroskedasticitu,odhadnite model znovu pouťitím Whitovho odhadu kovariančnej matice. Pouťite tento Whitov odhad na testovanie signifikancie parametrov a regresie a na testovane ostatných hypotéz o parametroch modelu. V opačnom prípade povrdíte pôvodné výsledky.
Modely:
- počet husí v kŕdli, druhý pozorovatež, testovanie nevychýlenosti jeho odhadu
- produkčná funkcia, testovanie kontatných výnosov z rozsahu
- otvorenosť ekonomiky z prvej DÚ, test o nezávislosti otvorenosti ekonomiky od jej veľkosti
- model z vášho projektu. (Povinnou súčasťou projektu sú dve verzie Whitovho testu a korekcia testov o parametroch, ak je potrebná. Ďalšie zisťovanie prítomnosti heteroskedasticity a jej príčin je jednou z možností, čo robiť v rámci samostatnej práce s modelom.)

Beáta Stehlíková (www)
Cvičenia z ekonometrie, LS 2008/2009