Cvičenie 5: Závislosť ceny opcie od parametrov. Put opcie
Závislosť ceny call opcie od volatility akcie
- Na predchádzajúcom cvičení a v DÚ: graf závislosti, ekonomická interpretácia.
- Dokážeme uvedenú monotónnu závislosť analyticky - vypočítame deriváciu a určíme jej znamienko (Derivácia distibučnej funkcie je funkcia hustoty)
- Aká je limita ceny opcie, ak volatilita ide do nekonečna? (Hypotéza na základe grafu a analytický dôkaz.)
- Aká je limita ceny opcie, ak volatilita ide k nule? (Hypotéza na základe grafu a analytický dôkaz.) Prečo je logické, že táto limita závisí od vzťahu aktuálnej ceny akcie a expiračnej ceny?
Závislosť ceny call opcie od ceny akcie
-
Na základe grafu môžeme vysloviť niekoľko hypotéz:
- V je rastúca funkcia S
- Ak S
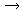 0, tak V
0, tak V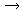 0.
0.
- Ak S
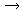
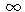 , tak sa cena opcie približuje k payoff diagramu, takže by mohlo platiť
, tak sa cena opcie približuje k payoff diagramu, takže by mohlo platiť
- Ekonomická interpretácia:
- Ak sa cena akcie blíži k nule, znižuje sa pravdepodobnosť, že opciu uplatníme - opcia sa stáva bezcennou.
- Ak S
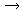
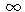 , tak
, tak
- Opcia sa zrejme bude realizovať, teda v čase expirácie dostaneme akciu a zaplatíme E, po odúročení tejto platby na súčasnú hodnotu vyslovíme hypotézu
- Taká istá úvaha ako predtým, len dodáme, že pre S
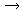
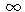 je E (aj súčasná hodnota) zanedbateľná, takže očakávame
je E (aj súčasná hodnota) zanedbateľná, takže očakávame
- Ak je vyššia súčasná cena akcie, zvyšuje sa pravdepodobnosť, že ju uplatníme a dosiahneme zisk. Rovnako sa zvyšuje pravdepodobnosť vysokých cien akcie, a teda vysokého zisku z realizácie opcie.
- Matematicky:
- Vypočítame limitu V pre S
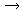 - ukážeme, že sa rovná 0.
- ukážeme, že sa rovná 0.
- Platia všetky tri navrhnuté aproximácie pre S
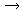
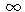 . Graficky vidíme, že sa líšia kvalitou aproximácie pre konečné hodnoty S.
. Graficky vidíme, že sa líšia kvalitou aproximácie pre konečné hodnoty S.
- Derivácia V podľa S je N(d1), čo je vždy kladné číslo. Teda V je rastúcou funkciou premennou S.
Závislosť ceny call opcie od expiračnej ceny
- V poslednej úlohe: graf závislosti
- Teraz: výpočet derivácie, jej znamienko.
Závislosť ceny call opcie od času do expirácie
Úlohy:
- Graf závislosti: čas do expirácie na x-ovej osi, cena opcie na y-ovej osi
- Výpočet derivácie, jej znamienko.
Závislosť ceny call opcie od úrokovej miery
Úlohy:
- Graf závislosti: úroková miera na x-ovej osi, cena opcie na y-ovej osi
- Výpočet derivácie, jej znamienko.
Výsledky derivovania
Put opcie
- Call-put parita:
- Uvažujme portfólio zložené z mínus jednej call opcie, jednej put opcie (na tú istú akciu, s rovnakou expiračnou cenou E a rovnakým expiračným časom) a jednej príslušnej akcie.
- V čase expirácie je hodnota portfólia E.
- Preto ak do expirácie zostáva čas
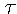 , hodnota portfólia je
, hodnota portfólia je 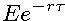 - cenu callu poznáme, takže môžeme vyjadriť cenu putu.
- cenu callu poznáme, takže môžeme vyjadriť cenu putu.
- Nakreslite cenu put opcie v závislosti od aktuálnej ceny akcie pre zvolené hodnoty parametrov.
- Vypočítajte limitu ceny put opcie pre S
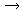
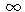 a pre S
a pre S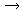 0.
0.
- Dokážte, že graf ceny put opcie v závislosti od aktuálnej ceny akcie vždy pretne payoff diagram.
- Ako závisí cena put opcie od parametrov?
Cvičenia z finančných derivátov
Beáta Stehlíková, 2007
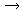 0, tak V
0, tak V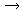 0.
0.
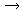
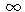 , tak sa cena opcie približuje k payoff diagramu, takže by mohlo platiť
, tak sa cena opcie približuje k payoff diagramu, takže by mohlo platiť
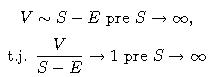
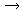
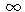 , tak
, tak
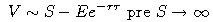
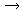
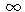 je E (aj súčasná hodnota) zanedbateľná, takže očakávame
je E (aj súčasná hodnota) zanedbateľná, takže očakávame
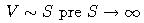
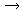 - ukážeme, že sa rovná 0.
- ukážeme, že sa rovná 0.
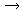
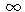 . Graficky vidíme, že sa líšia kvalitou aproximácie pre konečné hodnoty S.
. Graficky vidíme, že sa líšia kvalitou aproximácie pre konečné hodnoty S.
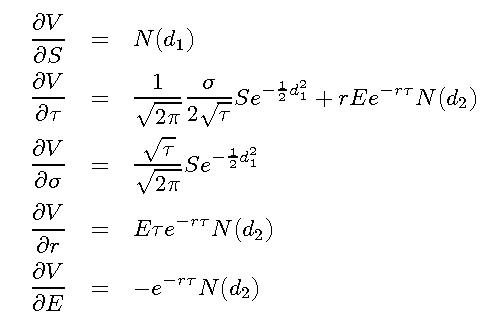
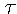 , hodnota portfólia je
, hodnota portfólia je 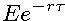 - cenu callu poznáme, takže môžeme vyjadriť cenu putu.
- cenu callu poznáme, takže môžeme vyjadriť cenu putu.