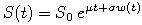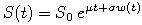Opakovanie - geometrický Brownov pohyb ako model pre vývoj ceny akcie
- Predpokladajme, že vývoj ceny akcie S je daný procesom:
- Dokážte, že pri takomto modeli sú výnosy počítané ako
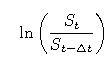 nezávislé a majú normálne rozdelenie.
nezávislé a majú normálne rozdelenie.
- Ako sa parametre normálneho rozdelenia z predchádzajúcej otázky dajú použiť na odhadnutie parametrov procesu pre vývoj akcie?
- Napíšte proces v tvare stochastickej diferenciálnej rovnice dS(t) = ... dt + ... dw(t).
-
Predpokladajme, že pre vývoj ceny akcie platí
kde mi = 0.35, sigma = 0.25 Súčasná cena akcie je 253.1 USD.
Vypočítajte
- strednú hodnotu ceny akcie o dva roky
- pravdepodobnosť, že o rok bude cena akcie menšia, ako je teraz
- pravdepodobnosť, že o pol roka bude cena akcie menšia ako 230 USD.
-
Predpokladajme, že pre vývoj ceny akcie platí
Uvažujme cenu akcie o t rokov a pravdepodobnosť, že v tomto čase bude cena akcie menšia ako súčasná. Ako táto pravdepodobnosť závisí od t. Intuitívne: Deterministická časť procesu je exponenciálny rast, takže táto pravdepodobnosť by sa mala zmenšovať. Na druhej strane, je tu dlhší čas na to, aby nastala nejaká výrazná odchýlka od trendu smerom nadol, spôsobená náhodnou časťou procesu. Ako je to?
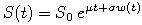
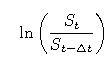 nezávislé a majú normálne rozdelenie.
nezávislé a majú normálne rozdelenie.