Cvičenie 1: Akcie. Stochastické procesy
Burzy - stránky:
Vývoj cien akcií
Na stránke Chicago Board Options Exchange zvoľte v menu Quotes - Delayed Quotes Beta.
Tu vyberte Advanced Charts.
Zadajte kód firmy (napr. IBM, MSFT = Microsoft, GM = General Motors,
...), pre ktorú chcete zobraziť ceny akcií. Môžete napísať aj názov
firmy, dostanete zoznam firiem, z ktorého vyberiete tú, ktorú chcete
zobraziť.
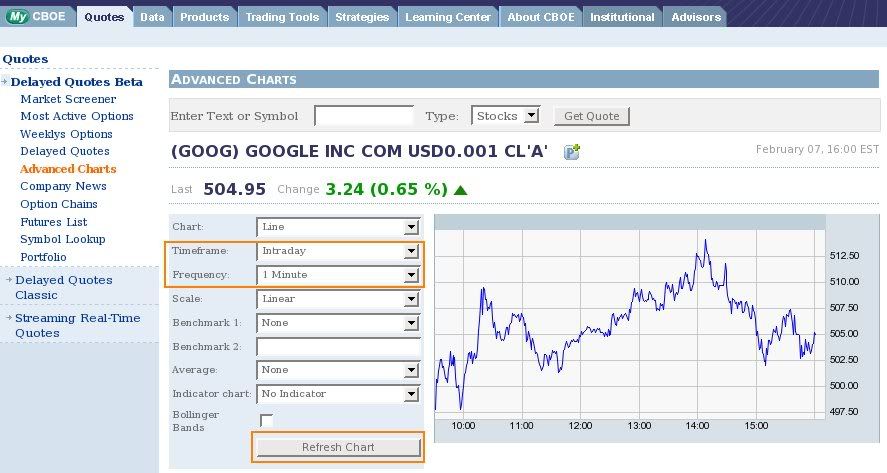
Teraz môžete meniť hodnoty Timeframe a Frequency. Kliknutím na Refresh chart dostanete príslušný graf.
Cvičenie 1
Zobrazte niekoľko grafov pre akcie zvolenej firmy tak, aby ste videli dlhodobý trend aj fluktuácie počas krátkeho obdobia.
|
Výnosy akcií
- Ak ceny akcií označíme S (s prísluąným časovým indexom), tak výnosy sú
Na modelovanie výnosov sa pouľíva veličina
posledná aproximácia vyplýva z toho, ľe
Cvičenie 2
V súbore google.txt
sú denné ceny akcií firmy Google od 7. februára 2007 do 7. februára
2008.
- Načítajte do Matlabu ceny akcie. Vytvorte vektor výnsov.
- Zobrazte
- vývoj cien akcie v čase,
- vývoj výnosov v čase,
- histogram výnosov.
|
Model pre výnosy akcií:
- sú nezávislé,
- majú normálne rozdelenie.
Wienerov proces
- Z priebehu cien akcií je vidieť náhodnosť, ktorá spôsobuje, že vývoj cien sa nedá modelovať deterministickou funkciou.
Preto sa používajú stochastické procesy.
- Wienerov proces je základným procesom, z ktorého sú odvodené mnohé ďalšie.
- Definícia. Proces w(t) s nasledovnými vlastnosťami sa nazýva Wienerov proces:
- Prírastky w(t+
 )-w(t) majú normálne rozdelenie s nulovou strednou hodnotou a disperziou
)-w(t) majú normálne rozdelenie s nulovou strednou hodnotou a disperziou  .
.
- Pre všetky t1 < t2 < ... < tn sú prírastky
w(t2) - w(t1), ..., w(tn) - w(tn-1)
nezávislé náhodné premenné.
- Proces začína v nule, t.j. w(0)=0.
- Trajektórie procesu sú spojité.
- Ako získať realizáciu Wienerovho procesu:
- Budeme generovať aproximáciu - hodnoty v diskrétnych bodoch typu (čas, hodnota), ktoré pospájame.
- Hodnoty budú v bodoch 0,
 ,2
,2 , . . ., kde
, . . ., kde  je dostatočne malý časový krok.
je dostatočne malý časový krok.
- Hodnota v čase 0 je 0.
- Prírastok na intervale [k
 , (k + 1)
, (k + 1) ] je náhodná premenná s nulovou strednou hodnotou
a varianciou
] je náhodná premenná s nulovou strednou hodnotou
a varianciou  .
.
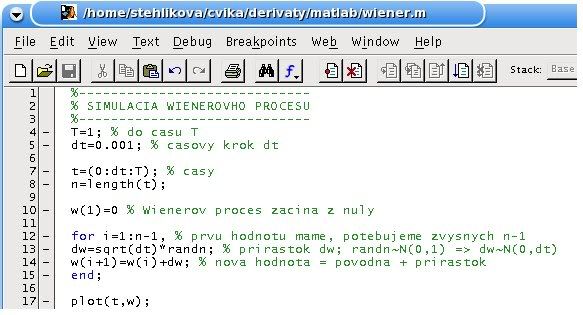
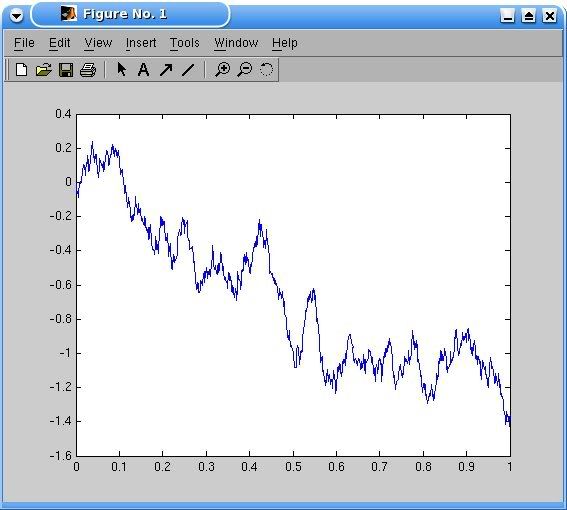
- V Matlabe:
- Kód:
a výstup:
- Funkcie Matlabu na prácu s vektormi sú efektívnejšie ako cykly:
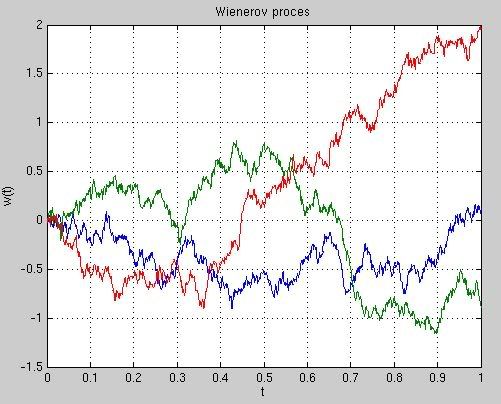
Cvičenie 3
Zakreslite do jedného grafu niekoľko realizácií Wienerovho procesu.
|
Násobok Wienerovho procesu
- Uvažujme násobok Wienerovho procesu, teda proces tvaru
Cvičenie 4
- Odvoďte rozdelenie prírastkov tohto procesu.
- Na základe výsledku predchádzajúcej úlohy vygenerujte realizácie procesu pre zvolenú hodnotu parametra a zobrazte ich priebeh.
|
- Závislosť od parametra
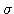 :
:
Cvičenie 5
-
Aké je pravdepodobnostné rozdelenie hodnoty procesu v čase 1? Ako závisí od parametra
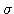 ? ?
-
Aké je pravdepodobnostné rozdelenie hodnoty procesu v čase t?
|
Brownov pohyb
- K násobku Wienerovho procesu pridáme lineárny trend:
Tento proces sa nazýva Brownov pohyb.
- Ak je parameter
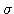 nulový, grafom je priamka. Pre nenulovú hodnotu
nulový, grafom je priamka. Pre nenulovú hodnotu 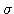 sa k tomuto lineárnemu trendu pridávajú náhodné fluktuácie.
sa k tomuto lineárnemu trendu pridávajú náhodné fluktuácie.
Cvičenie 6
- Odvoďte rozdelenie prírastkov tohto procesu.
- Na základe výsledku predchádzajúcej úlohy vygenerujte realizácie procesu pre zvolené hodnoty parametrov a zobrazte ich priebeh.
Ako sa mení typický priebeh procesu, keď meníme hodnoty parametrov?
|
Cvičenie 7
Aké je pravdepodobnostné rozdelenie hodnoty Brownovho pohybu v čase t?
|
Cvičenie 8
Vygenerujte 1000 realizácií Brownovho porcesu so zvolenými
parametrami. V každom čase vypočítajte priemer a výberovú disperziu z
vygenerovaných dát. Zakreslite ich do grafov (x-ová os: čas, y-ová os:
na prvom grafe priemer, na druhom grafe výberová disperzia) a
porovnajte so skutočnou strednou hodnotou a disperziou.
|
Cvičenie 9
Vygenerujte niekoľko realizácií posunutého Brownovho pohybu, ktorý v čase 0 začína vo zvolenom bode x0 (prírastky má rovnaké ako Brownov pohyb) a zobrazte ich priebeh v jednom grafe.
Aké je pravdepodobnostné rozdelenie tohto procesu v čase t?
|
Geometrický Brownov pohyb
- Geometrický Brownov pohyb je proces
Hodnota x0 predstavuje hodnotu procesu v čase 0.
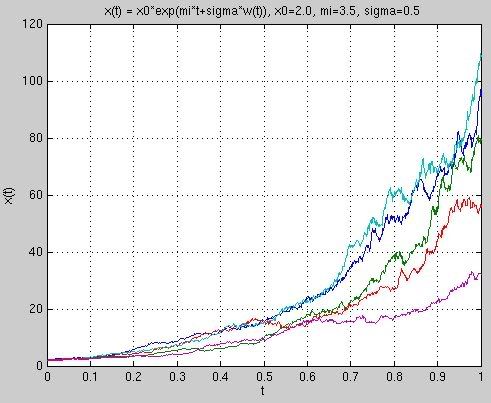
Cvičenie 10
Vygenerujte niekoľko realizácií geometrického Brownovho pohybu so
zvolenými parametrami. Ako sa mení typický priebeh procesu, keď meníme
hodnoty parametrov?
|
Lognormálne rozdelenie
- Náhodná premenná X má lognormálne rozdelenie, ak náhodná premenná ln(X) má normálne rozdelenie
 .
.
- Hustota náhodnej premennej X s lognormálnym rozdelením je
- Stredná hodnota a disperzia náhodnej premennej X s lognormálnym rozdelením je
Cvičenie 11
Ukážte, že hodnota geometrického Brownovho pohybu v čase t je
náhodná premenná s lognormálnym rozdelením. Aké sú parametre tohto
rozdelenia?
|
Geometrický Brownov pohyb ako model pre vývoj ceny akcie
- Povedali sme, že výnosy cien akcií sa modelujú ako nezávislé náhodné premenné s normálnym rozdelením.
- Ak sa cena akcie riadi geometrickým Brownovym pohybom, tak výnosy majú uvedenú vlastnosť.
Cvičenie 12
Dokážte toto tvrdenie.
|
- Ako získať parametre geometrického Brownovho pohybu modelujúceho cenu akcie z dát
- Ak proces pre cenu akcie je
tak
- Odhad parametrov
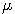 a
a 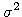 procesu dostaneme odhadnutím parametrov tohto normálneho rozdelenia.
procesu dostaneme odhadnutím parametrov tohto normálneho rozdelenia.
Cvičenie 13
Uvaľujme rok ako jednotku času (t.j. t = 1 znamená jeden rok) a  =1/250. Z dát firmy Google z tohto cvičenia odhadnite parametre geometrického Brownovho pohybu, ktorým modelujeme vývoj týchto cien. =1/250. Z dát firmy Google z tohto cvičenia odhadnite parametre geometrického Brownovho pohybu, ktorým modelujeme vývoj týchto cien.
|
Cvičenie 14
Predpokladajme, že sa cena akcie riadi geometrickým Brownovym
pohybom s uvedenými parametrami. 7.2.2008 bola jej cena 504.95 USD.
- Nájdite strednú hodnotu a zobrazte graf pravdepodobnostného rozdelenia ceny tejto akcie o štvrť roka.
- Aká je pravdepodobnosť, že o rok bude cena tejto akcie nižšia ako je súčasná?
- Aká je pravdepodobnosť, že o pol roka bude cena vyššia ako 600 USD?
|
Cvičenia z finančných derivátov
Beáta Stehlíková, 2008


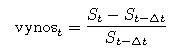
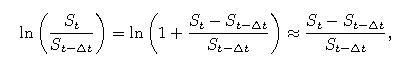
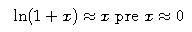
 )-w(t) majú normálne rozdelenie s nulovou strednou hodnotou a disperziou
)-w(t) majú normálne rozdelenie s nulovou strednou hodnotou a disperziou  .
.
 ,2
,2 , . . ., kde
, . . ., kde  je dostatočne malý časový krok.
je dostatočne malý časový krok.
 , (k + 1)
, (k + 1) ] je náhodná premenná s nulovou strednou hodnotou
a varianciou
] je náhodná premenná s nulovou strednou hodnotou
a varianciou  .
.


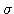 :
:

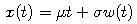
 nulový, grafom je priamka. Pre nenulovú hodnotu
nulový, grafom je priamka. Pre nenulovú hodnotu 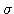 sa k tomuto lineárnemu trendu pridávajú náhodné fluktuácie.
sa k tomuto lineárnemu trendu pridávajú náhodné fluktuácie.

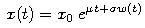
 .
.
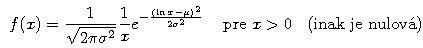

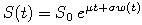
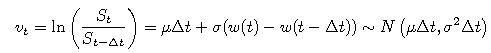
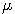 a
a 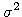 procesu dostaneme odhadnutím parametrov tohto normálneho rozdelenia.
procesu dostaneme odhadnutím parametrov tohto normálneho rozdelenia.
 =1/250. Z dát firmy Google z tohto cvičenia odhadnite parametre geometrického Brownovho pohybu, ktorým modelujeme vývoj týchto cien.
=1/250. Z dát firmy Google z tohto cvičenia odhadnite parametre geometrického Brownovho pohybu, ktorým modelujeme vývoj týchto cien.