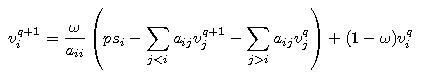Cvičenie 11: Black - Scholesova rovnica: numerické riešenie (2)
Otázky, ktoré budeme chcieť zodpovedať:
- Čo nám zaručí, že Gauss-Seidelova metóda, ktorú pri numerickom riešení Black-Scholesovej rovnice používame, konverguje?
- Dokážeme, že pre diagonálne dominantnú maticu Gauss-Seidelova metóda konverguje.
- Overenie tejto podmienky pre našu maticu je jednoduché.
- Od čoho závisí rýchlosť konvergencie metódy?
- Zopakujeme si, čo je spektrálny polomer matice a aký je jeho vzťah s normou mocnín matice.
- Ukážeme, ako rýchlosť konvergencie súvisí so spektrálnym polomerom iteračnej matice.
- Ako sa dá urýchliť konvergencia Gauss-Seidelovej metódy?
- SOR metóda (successive over relaxation):
kde omega je parameter ( omega > 1 - over relaxation, omega < 1 - under relaxation).
- Bez dôkazu uvedieme nasledovné tvrdenia týkajúce sa konvergencie tejto metódy:
- Na to, aby SOR metóda konvergovala, musí byť parameter omega z intervalu (0,2).
- Pre sústavu z numerického riešenia BS rovnice konverguje SOR metóda pre ľubovoľné omega z intervalu (0,2).
- Aká je optimálna hodnota parametra omega?
Nasledujúca úloha bude súčasťou domácej časti druhej písomky, odovzdávať sa bude na konci semestra:
Cvičenia z finančných derivátov
Beáta
Stehlíková, 2008