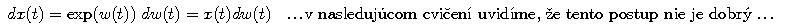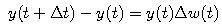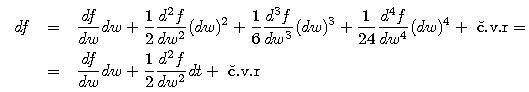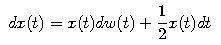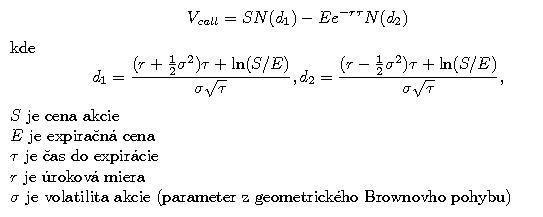|
Robert C. Merton (1944 - ), Myron S. Scholes (1941 - )
Cena Švédskej banky za ekonómiu, 1997
Zo stránky
Jokes about economists and economics, vraj skutočná udalosť ;)
An economist was about to give a presentation in Washington, DC on the problems with Black-Scholes model of option pricing and was expecting no more than a dozen of government officials attending (who would bother?). To his amazement, when he arrived, the room was packed with edgy, tough-looking guys in shades. Still, after five or so minutes into the presentation all of them stood up and left without a word. The economist found out only later
that his secretary ran the presentation through a spell-checker and what was "The Problem with Black-Scholes" became "The Problem with Black Schools", a rather more fascinating subject.
|
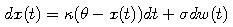
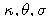 sú kladné konštatny
sú kladné konštatny