
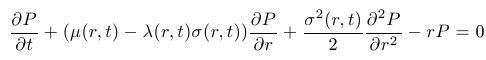
V čase expirácie je hodnota dlhopisu rovná jednej, teda P(T,r)=1 pre každé r.


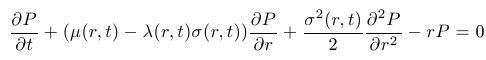
V čase expirácie je hodnota dlhopisu rovná jednej, teda P(T,r)=1 pre každé r.

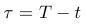
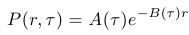
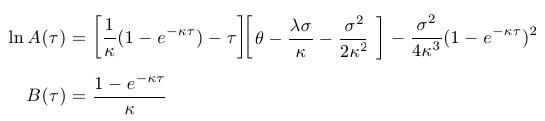
|
Cvičenie 1 Zvožte si parametre Vašíčkovho modelu článku z minulého cvičenia. Zvoľte si hodnotu okamžitej úrokovej miery a zakreslite výnosové krivky pre niekoľko rôznych trhových cien rizika. |
|
Cvičenie 2 Zvožte si parametre Vašíčkovho modelu článku z minulého cvičenia. Zvoľte si hodnotu trhovej ceny rizika. Pre niekoľko hodnôt okamžitej úrokovej miery zakreslite do jedného grafu výnosové krivky. Dokážte, že ak tau ide do nekonečna, tak úrokové miery so splatnosťou tau konvergujú k hodnote 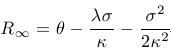
|
|
Cvičenie 3 Zvožte si parametre Vašíčkovho modelu článku z minulého cvičenia. Predpokladjme, že limita výnosových kriviek sa rovná trom štvrtinám limitnej hodnoty okamžitej úrokovej miery. Vypočítajte trhovú cenu rizika. |
|
Cvičenie 4 Otázka o Vašíčkovom modeli z internetového diskusného fóra: 
|
|
Cvičenie 5 Stiahnite si dáta - okamžitú úrokovú mieru a výnosové krivky. Z časového radu okamžitej úrokovej miery odhadnite parametre Vašíčkovho modelu. Potom odhadnite trhovú cenu rizika tak, aby ste minimalizovali súčet druhých mocnín rozdielov skutočných úrokových mier a úrokových mier z Vašíčkovho modelu, pričom rozdiel zodpovedajúci maturite tau vstupuje do účelovej funkcie s váhou tau2. (To znamená, že dôležitejšia je zhoda úrokových mier s dlhšou splatnosťou.) Porovnajte skutočné výnosové krivky s Vašíčkovymi. Považujete zhodu za dobrú? |
Cvičenie
|