Náhodné procesy, modelovanie cien akcií
:: Stochastický vývoj finančných veličín ::
Z priebehov cien akcií (ako aj iných finančných veličín - úrokových mier, výmenných kurzov, ...) vidíme, že ich priebeh sa nedá popísať deterministickou funkciou. Preto sa na ich modelovanie používajú náhodné procesy.Vľavo: trend (vývoj ceny počas posledného roka), vpravo: fluktuácie (vývoj ceny počas jedného dňa):
Zdroj: http://finance.google.com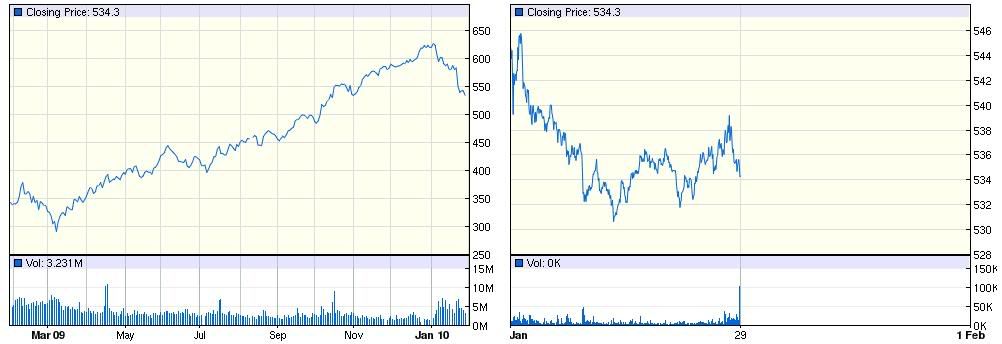
:: Wienerov proces a Brownov pohyb ::
-
Základným náhodným procesom, z ktorého sú ostatné odvodené, je Wienerov proces. Pripomeňme si jeho definíciu:
Systém X(t) náhodných premenných sa nazýva Wienerov proces, ak- prírastky
X(t+
 ) - X(t)
majú normálne rozdelenie s nulovou strednou hodnotou a s disperziou
) - X(t)
majú normálne rozdelenie s nulovou strednou hodnotou a s disperziou  ,
,
- pre každé delenie 0 = t0 < t1 < ... < tn sú prírastky Xti+1 - Xti nezávislé náhodné premenné s parametrami podľa predchádzajúceho bodu,
- X(0)=0,
- trajektórie sú spojité.
- prírastky
X(t+
-
Ako získame realizáciu Wienerovho procesu?
- Budeme generovať aproximáciu - hodnoty v diskrétnych bodoch typu (čas, hodnota), ktoré pospájame.
- Hodnoty budú v bodoch 0,
 ,2
,2 , . . ., kde
, . . ., kde  je dostatočne malý časový krok.
je dostatočne malý časový krok.
- Hodnota v čase 0 je 0.
- Prírastok na intervale [k
 , (k + 1)
, (k + 1) ] je náhodná premenná s nulovou strednou hodnotou
a varianciou
] je náhodná premenná s nulovou strednou hodnotou
a varianciou  .
.
V Matlabe:
%------------------------------- % SIMULACIA WIENEROVHO PROCESU %------------------------------- T=1; % do casu T dt=0.001; % casovy krok dt t=(0:dt:T) % vektor casov, v ktorych generujeme hodnoty procesu n=length(t); w(1)=0; % Wienerov proces zacina z nuly for i=1:n-1 % prvu hodnotu mame, potrebujeme zvysnych n-1 dw=sqrt(dt)*randn; % prirastok dw; randn ~ N(0,1) => dw ~ N(0,dt) w(i+1)=w(i)+dw; % nova hodnota = povodna + prirastok end; plot(t,w); % vykreslime priebeh
Poznamenajme, že na zrýchlenie výpočtov v Matlabe sa dajú využiť funkcie pre prácu s vektormi (namiesto cyklov):
%---------------------------------------- % RYCHLEJSIA SIMULACIA WIENEROVHO PROCESU %---------------------------------------- T=1; % do casu T dt=0.001; % casovy krok dt t=(0:dt:T) % vektor casov, v ktorych generujeme hodnoty procesu n=length(t); dw=sqrt(dt)*randn(n-1,1); % vektor prirastkov - nezavisle N(0,dt) w=[0;cumsum(dw)]; % zaciname z nuly, dalek kumulativne sucty prirastkov plot(t,w); % vykreslime priebeh
Ukážka výstupu: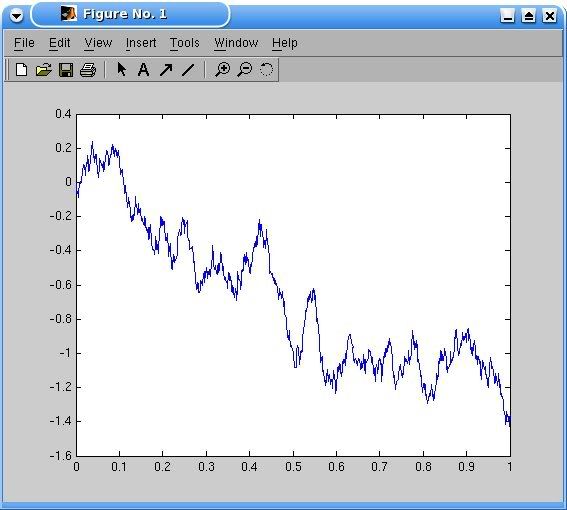
-
Ak k násobku Wienerovho procesu pridáme lineárny trend:
dostávame proces, ktorý sa nazýva Brownov pohyb. Ak je parameter
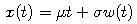
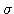 nulový, grafom je priamka. Pre nenulovú hodnotu
nulový, grafom je priamka. Pre nenulovú hodnotu 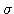 sa k tomuto lineárnemu trendu pridávajú náhodné fluktuácie.
sa k tomuto lineárnemu trendu pridávajú náhodné fluktuácie.
:: Cvičenia (1) ::
- Nakreslite do jedného grafu niekoľko realizácií Wienerovho procesu.
Ukážka výstupu: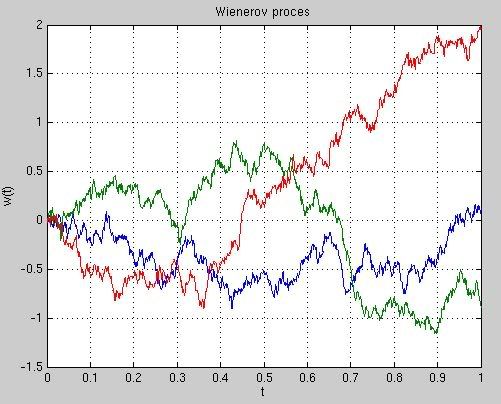
- Nech W je Wienerov proces. Nájdite pravdepodobnostné rozdelenie W(t).
Návod: Wienerov proces začína v nule, takže W(t) = W(t) - W(0).
- Nájdite pravdepodobnostné rozdelenie Brownovho procesu v čase t.
- Nakreslite do jedného grafu niekoľko realizácií Brownovho pohybu.
Ukážka výstupu:
Ako závisí typický priebeh procesu od parametrov?
- Nech W je Wienerov proces. Nájdite pravdepodobnostné rozdelenie náhodnej premennej W(2) + W(3).
Návod: Napíšte túto náhodnú premennú ako lineárnu kombináciu nezávislých prírastkov. K dispozícii máme časy 2, 3 a 0 (vtedy je hodnota procesu nulová), takže pôjde zrejme o prírastky W(3) - W(2) a W(2) - W(0).
- Nech W je Wienerov proces a nech s < t. Vypočítajte kovarianciu W(s) a W(t).
Návod: Použite podobný postup ako v predchádzajúcom príklade.
- Nech W je Wienerov proces. Nájdite pravdepodobnostné rozdelenie náhodného vektora (W(1), W(3)).
:: Geometrický Brownov pohyb ::
- Nech w je Wienerov proces. Potom geometrický Brownov pohyb je proces definovaný vzťahom
Hodnota x0 predstavuje hodnotu procesu v čase 0.
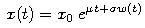
-
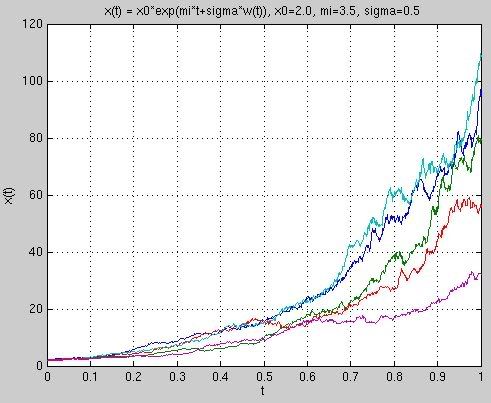
Ukážka trajektórií geometrického Brownovho pohybu:
- Pripomeňme si definíciu a základné vlastnosti lognormálneho rozdelenia:
- Náhodná premenná X má lognormálne rozdelenie, ak náhodná premenná ln(X) má normálne rozdelenie
 .
.
- Hustota náhodnej premennej X s lognormálnym rozdelením je
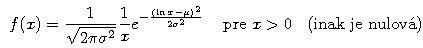
- Stredná hodnota a disperzia náhodnej premennej X s lognormálnym rozdelením je

- Náhodná premenná X má lognormálne rozdelenie, ak náhodná premenná ln(X) má normálne rozdelenie
:: Cvičenia (2) ::
- Ukážte, že hodnota geometrického Brownovho pohybu v čase t je náhodná premenná s lognormálnym rozdelením. Aké sú parametre tohto rozdelenia? Aká je stredná hodnota geometrického Brownovho pohybu v čase t ?
- Uvažujme geometrický Brownov pohyb z predchádzajúceho obrázku, t. j. x(t)=2*exp(3.5t+0.5w(t)), kde w je Wienerov proces. Zostrojte podobný obrázok s grafmi niekoľkých realizácií procesu a pridajte doňho aj strednú hodnotu.
:: Modelovanie cien akcií pomocou geometrického Brownovho pohybu ::
-
Cenu akcie S modelujeme geometrickým Brownovym pohybom:
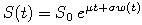
-
Na výpočet výnosov sa používa veličina
pričom posledná aproximácia vyplýva z toho, že
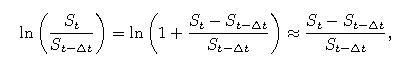
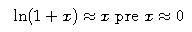
-
Ak sa cena akcie S riadi geometrickým Brownovym pohybom, tak pre výnosy dostávame
teda výnosy sú nezávislé náhodné premenné s normálnym rozdelením a uvedenými parametrami.
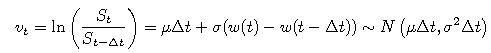
- Ako získať parametre geometrického Brownovho pohybu z dát - odhadom parametrov normálneho rozdelenia z výnosov.
:: Cvičenia (3) ::
- Predpokladajme, že cena akcie sa riadi geometrickým Brownovym pohybom s parametrami
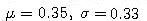 . Vypočítajte strednú hodnotu ceny akcie o pol roka, ak jej dnešná cena je 125 USD.
. Vypočítajte strednú hodnotu ceny akcie o pol roka, ak jej dnešná cena je 125 USD.
- Stiahnite si dáta o vývoji ceny vybranej akcie (http://finance.google.com, http://finance.yahoo.com) so zvolenou frekvenciou a časovým intervalom. Modelujte tento vývoj geometrickým Brownovym pohybom.
- Odhadnite jeho parametre.
- Aká je stredná hodnota ročného výnosu?
- Aká je pravdepodobnosť, že ročný výnos bude kladný?
- Aká je pravdepodobnosť, že o pol roka bude cena akcie menšia ako 80 percent dnešnej ceny?
:: Ďalšie príklady na precvičenie ::
Vo všetkých úlohách označuje w(t) Wienerov proces.-
Priraďte nasledovné procesy ich simuláciám na grafe:
- x1(t) = 5 + 2t + 3w(t),
- x2(t) = - 2t + w(t),
- x3(t) = 5 + 2t + w(t),
- x4(t) = 2t + w(t).
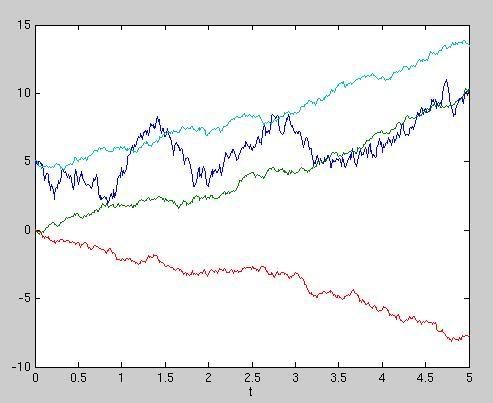
- Nájdite pravdepodobnostné rozdelenie nasledovných hodnôt:
- w(4)-w(2),
- w(2),
- 3+w(3),
- w(2)-2w(1).
- Definujme náhodný proces
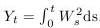 . Vypočítajte jeho strednú hodnotu a disperziu v čase t.
. Vypočítajte jeho strednú hodnotu a disperziu v čase t.
- Pomocou Wienerovho procesu W definujme nový náhodný proces vzťahom Dokážte, že je to tiež Wienerov proces.
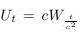
Návod: Treba overiť vlastnosti Wienerovho procesu z definície.
- Pre t z intervalu [0,1] definujme proces
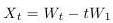 .
.
- Vygenerujte niekoľko jeho trajektórií a zakreslite ich do grafu.
- Vypočítajte jeho strednú hodnotu v čase t
- Vypočítajte kovarianciu medzi jeho hodnotami v časoch t a s.
- Uvažujme proces
x(t) = 2 - 5 t + 2 w(t). Zobrazte do jedného grafu:
- päť realizácií
- strednú hodnototu procesu
- strednú hodnotu +/- 1.96*štandardnú odchýlku (t.j. 95 percentný interval spoľahlivosti)
Ukážka možného výstupu: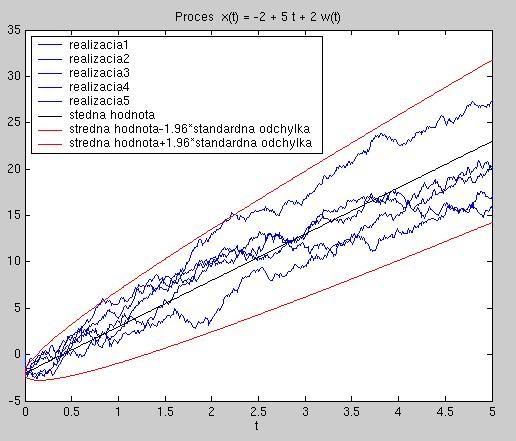
-
Predpokladajme, že cena akcie sa riadi geometrickým Brownovym pohybom s parametrami
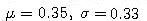 . Dnešná cena akcie je 250 USD.
. Dnešná cena akcie je 250 USD.
- Nakreslite graf hustoty ceny akcie o rok. Vypočítajte jej strednú hodnotu.
- Aká je stredná hodnota mesačného výnosu?
- Aká je pravdepodobnosť, že mesačný výnos bude kladný?
- Aká je pravdepodobnosť, že o dva mesiace bude cena akcie z intervalu [270, 280]?
- Čo si myslíte, čo je na obrázku na obale tejto knihy?

Beáta Stehlíková (www)
Cvičenia z finančných derivátov, FMFI UK Bratislava, LS 2009/2010