Modelovanie úrokových mier - Vašíčkov model
:: Jednofaktorový short rate model ::
- Short rate - okamžitá úroková miera, aproximuje sa úrokovou mierou s krátkoui splatnosťou
- Okamžitá úroková miera sa modeluje stochastickou diferenciálnou rovnicou:
teda trend vo vývoji úrokovej miery + náhodné fluktuácie okolo trendu

- Jednofaktorový model - jedna stochastická diferenciálna rovnica pre r, t. j. jeden zdroj náhodnosti vo vývoji okamžitej úrokovej miery (jeden Wienerov proces).
:: Vašíčkov model ::
- Stochastická diferenciálna rovnica pre okamžitú úrokovú mieru:
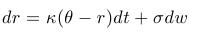
- Vlastnosť mean-reversion (priťahovanie k dlhodobej hodnote, k limitnej hodnote) - pre strednú hodnotu platí:
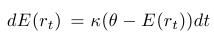
- Volatilita je konštantná, nezávisí teda od aktuálnej hodnoty úrokovej miery
:: Pravdepodobnostné rozdelenie úrokových mier ::
- Podmienené rozdelenie úrokovej miery, ak poznáme jej hodnotu r0 v čase 0 je normálne rozdelenie
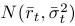 s parametrami
s parametrami
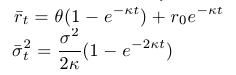
- Znalosť tohoto rozdelenia nám umožňuje:
- Vygenerovať realizáciu procesu pre zadané parametre a začiatočnú hodnotu úrokovej miery.
- Odhadovať parametre procesu z dát.
- Upozornenie: V literatúre sa požívajú rôzne označenia pre lineárnu funkciu driftu, treba si vždy pozrieť, s akým driftom sa pracuje.
::Cvičenia (1) ::
Otvorte si pdf súbor s článokom Athanasios Episcopos: Further evidence on alternative continuous time models of the short-term interest rate. Journal of International Financial Markets, Institutions and Money 10 (2000) 199 ? 212.Parametrizácia modelu - rovnica (1) v článku:
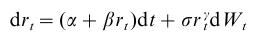
V tabuľke 3 sú odhadnuté parametre modelov tohto tvaru pre niekoľko štátov. Vyberte si štát a nájdite odhady parametrov Vašíčkovho modelu. Tieto hodnoty použite na riešenie nasledujúcich úloh.
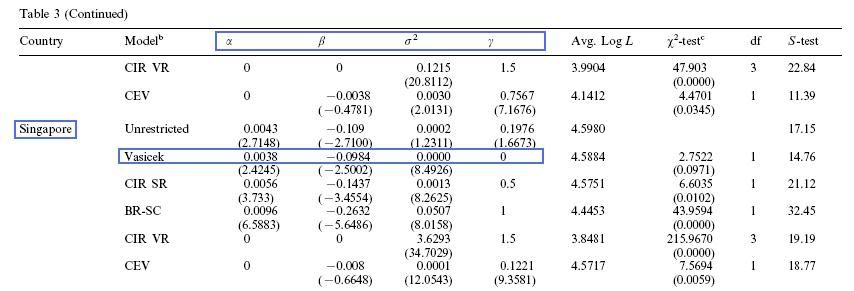
-
Transformujte tieto hodnoty na parametre kapa, theta (parameter sigma je v oboch prípadoch rovnaký).
- Zvoľte si začiatočnú hodnotu úrokovej miery a nakreslite do jedného grafu niekoľko realizácií ďalšieho vývoja (napr. počas nasledujúceho roka) s časovým krokom jeden deň, spolu s jeho strednou hodnotou.
- Predpokladajte, že dnešná hodnota úrokovej miery je 4.5 percenta. Aká je stredná hodnota úrokovej miery o týždeň, o mesiac a o rok? Zostrojte pre tieto úrokové miery intervalové odhady (stredná hodnota +/- 2*štandardná odchýlka).
- Aké je limitné rozdelenie úrokovej miery. Nakreslite graf hustoty tohto limitného rozdelenia. Doplňte do grafu hustoty rozdelenia úrokovej miery o mesiac, o rok, ... - tak, aby ste videli konvergenciu týchto hustôt k limitnej hustote.
- Jednou z nevýhod Vašíčkovho modelu je možnosť záporných úrokových mier. Vypočítajte pravdepodobnosť zápornej úrokovej miery v nasledovných prípadoch:
- limitné rozdelenie úrokovej miery
- úroková miera o mesiac, ak jej dnešná hodnota je 5 percent.
- úroková miera o mesiac, ak jej dnešná hodnota je pol percenta.
- úroková miera o týždeň, ak jej dnešná hodnota je 5 percent.
- úroková miera o týždeň, ak jej dnešná hodnota je pol percenta.
- Nájdite príklad takých parametrov, aby predchádzajúce pravdepodobnosti záporných úrokových mier boli väčšie (pri takýchto pravdepodobnostiach zrejme nie je model vhodný).
:: Ďalšie príklady na precvičenie ::
- Odhadovanie parametrov Vašíčkovho modelu.
Na písomke nebude, ale ak chcete počítať pravdepodobnosti s aktuálnymi hodnotami parametrov, môžete ich získať napríklad týmto spôsobom.
Podmienené rozdelenie úrokových mier je normálne, preto funkcia vierohodnostije súčin hustôt normálnych rozdelení.
Zdroj: Damiano Brigo, Fabio Mercurio: Interest Rate Models - Theory and Practice. Second Edition. Springer, 2007. Kapitola 3.1.2, str. 61-62.
- Stiahnite si dáta úrokovej miery (napr. 3M treasury bills, Euribor s krátkou dobou splatnosti a pod.) zo zvoleného časového intervalu. Zobrazte ich vývoj.
Zdroje dát: - Odhadnite parametre a transformujte ich na parametre kapa, theta, sigma.
- Pre zvolenú začiatočnú hodnotu úrokovej miery nakreslite do jedného grafu strednú hodnotu jej ďalšieho vývoja a niekoľko simulácií.
- Nájdite limitné rozdelenie úrokovej miery.
- Stiahnite si dáta úrokovej miery (napr. 3M treasury bills, Euribor s krátkou dobou splatnosti a pod.) zo zvoleného časového intervalu. Zobrazte ich vývoj.
- Stiahnite si dáta - trojmesačné výnosy treasury bills od začiatku roka 2008, týždenné dáta.
Link: http://www.federalreserve.gov/releases/h15/data.htm.
Dáta sú úrokové miery v percentách, preveďte ich na desatinné číslo.- Z dát z roku 2008 odhadnite parametre Vašíčkovho modelu.
- Vypočítajte strednú hodnotu a 95 percentný interval spoľahlivosti na základe posledného pozorovania v roku 2008 pre vývoj úrokovej miery v roku 2009.
- Nakreslite do jedného grafu - vývoj v roku 2008, strednú hodnotu a interval spoľahlivosti z predchádzajúcej úlohy, tri realizácie vývoja v roku 2009.
- Nakreslite do jedného grafu - vývoj v roku 2008, strednú hodnotu a interval spoľahlivosti z predchádzajúcej úlohy, a skutočný vývoj v roku 2009.
- Nájdite limitné rozdelenie úrokovej miery. Aká je pravdepodobnosť zápornej úrokovej miery pri tomto rozdelení?
Beáta Stehlíková (www)
Cvičenia z finančných derivátov, FMFI UK Bratislava, LS 2009/2010