Stochastické diferenciálne rovnice
:: Stochastické diferenciálne rovnice ::
- Nenáhodná funkcia môže byť zadaná ako riešenie obyčajnej diferenciálnej rovnice - máme daný vzťah medzi diferenciálom funkcie a diferenciálom času. Napr. dx(t)=x(t) dt, spolu so začiatočnou podmienkou x(0) určuje (deterministickú, t.j. nenáhodnú) funkciu x.
- Analógia pre náhodné funkcie - vzťah medzi diferenciálom funkcie, diferenciálom času a diferenciálom Wienerovho procesu dw. Takto dostávame stochastické diferenciálne rovnice. Ich riešením je náhodná funkcia. Napríklad:
- dx=2dt+3dw, začiatočná podmienka x(0)=0 - toto je Brownov pohyb: x(t)=2t+3w(t)
- dx=2dt+3dw, začiatočná podmienka x(0)=1 - posunutý Brownov pohyb, začína z jednotky: x(t)=1+2t+3w(t)
- dx=10[1-x(t)] dt + 0.25 dw(t), x(0)=0.5 - tiež sa dá zapísať explicitne, ale toto vyjadrenie je komplikovanejšie. Dobrú predstavu o priebehu takéhoto procesu však dostaneme pomocou simulácií jeho trajektórií.
- Pozrime sa teda na proces tvaru
kde

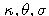 sú kladné konštanty. Takýto proces sa nazýva Ornstein-Uhlenbeckov proces.
sú kladné konštanty. Takýto proces sa nazýva Ornstein-Uhlenbeckov proces.
Najjednoduchším pôsobom, ako získať aproximáciu riešenia stochastickej diferenciálnej rovnice je nahradiť diferenciály diferenciami - analógia Eulerovej metódy pre obyčajné diferenciálne rovnice:
kappa=10; theta=1; sigma=0.25; % parametre procesu x0=0.5 % zaciatocna hodnota dt=0.001; % casovy krok n=1000; % pocet krokov % Eulerova schema x(1)=x0; for i=1:n dw=sqrt(dt)*randn; dx=kappa*(theta-x(i))*dt+sigma*dw; x(i+1)=x(i)+dx; end; t=0:dt:n*dt; % cas plot(t,x) - Terminológia: Deterministická časť procesu (pri časovom diferenciáli dt) sa nazýva drift, stochastická časť (pri diferenciáli Wienerovho procesu dw) sa nazýva volatilita.
:: Cvičenia (1) ::
-
Zakreslite do jedného grafu niekoľko realizácií Orstein-Uhlenbeckovho procesu na intervale [0,5] so zvolenými parametrami, ktoré začínajú z rôznych začiatočných hodnôt. Použite pritom časový krok 0.001.
- Uvažujme najskôr Ornstein-Uhlenbeckov proces s nulovou volatilitou - ako závisí jeho (teraz nenáhodný) priebeh od parametrov a od začiatočnej hodnoty? Ako ovplyvňuje priebeh procesu hodnota volatility?
- Ornstein-Uhlenbeckov proces sa používa napríklad pri modelovaní úrokových mier. Vašíčkov model predpokladá, že okamžitá úroková miera (prakticky - úroková miera na krátky čas) sa riadi Ornstein-Uhlenbeckovym procesom.
V článku Athanasios Episcopos: Further evidence on alternative continuous time models of the short-term interest rate. Journal of International Financial Markets, Institutions and Money 10 (2000) 199-212 autor odhadoval modely úrokových mier. Všeobecný model, ktorým sa zaoberal, jeŠpeciálnou voľbou niektorých parametrov dostávame konkrétne modely, jedným z nich je aj Vašíčkov model. Výsledky pre Nový Zéland (odhady parametrov pre mesačné dáta od apríla 1986 do apríla 1998 sú v nasledujúcej tabuľke:
Zdroj: (Episcopos, 1998)
Vygenerujte priebeh vývoja úrokovej miery na základe odhadnutých parametrov Vašíčkovho modelu. Zakreslite do jedného grafu niekoľko možných priebehov, štartujúcich z rovnakej začiatočnej hodnoty.
:: Itóova lema ::

|
Kijoši Itó (1915 - 2008), zakladateľ teórie stochastických diferenciálnych rovníc.
Životopis na stránke Inamori Foundation Životopis na "The MacTutor History of Mathematics archive" "Dr. Kiyoshi Ito receives the Gauss Prize" |
- Na predchádzajúcom cvičení sme mali predpis procesu (geometrický Brownov pohyb - cena akcie) x(t) zadaný explicitne v tvare x(t)=.... Na začiatku tohto cvičenia sma pracovali s iným zápisom - pomocou diferenciálov sme definovali Ornestein-Uhlenbeckov proces. Teraz si ukážeme ich vzájomný vzťah.
- Pre nenáhodnú funkciu vieme derivovaním napísať obyčajnú diferenciálnu rovnicu, ktorú spĺňa. Napr. pre x(t)=x2(t) platí dx(t)=2 x(t) dt. Naopak, pre zadanú obyčajnú diferenciálnu rovnicu vieme v niektorých prípadoch napísať explicitné riešenie.
- Ako derivovať náhodnú funkciu? Odpoveď dáva Itóova lema:
Nech x je proces daný rovnicoua f(t,x) je hladká funkcia. Potom f vyhovuje stochastickej diferenciálnej rovnici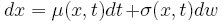
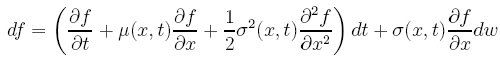
- Ukážky použitia Itóovej lemy pri oceňovaní derivátov:
- Vývoj ceny akcie je daný stochastickou diferenciálnou rovnicou pre S. Cena derivátu V závisí od času t a od ceny akcie S. Itóova lema dáva predpis pre stochastickú diferenciálnu rovnicu, ktorú spĺňa cena derivátu V(t,S). Táto rovnica sa využije pri odvodzovaní ceny derivátu.
- Vývoj okamžitej úrokovej miery r je daný stochastickou diferenciálnou rovnicou (napríklad Ornstein-Uhlenbeckov proces vo Vašičkovom modeli). Cena derivátu V závisí od času t a od okamžitej úrokovej miery r. Ďalej je postup analogický: Itóova lema dáva predpis pre stochastickú diferenciálnu rovnicu, ktorú spĺňa cena derivátu V(t,r). Táto rovnica sa využije pri odvodzovaní ceny derivátu.
|
In precisely built mathematical structures, mathematicians find the same sort of beauty others find in enchanting pieces of music, or in magnificent architecture. There is, however, one great difference between the beauty of mathematical structures and that of great art. Music by Mozart, for instance, impresses greatly even those who do not know musical theory; the cathedral in Cologne overwhelms spectators even if they know nothing about Christianity. The beauty in mathematical structures, however, cannot be appreciated without understanding of a group of numerical formulae that express laws of logic. Only mathematicians can read "musical scores" containing many numerical formulae, and play that "music" in their hearts. Accordingly, I once believed that without numerical formulae, I could never communicate the sweet melody played in my heart. Stochastic differential equations, called "Ito Formula," are currently in wide use for describing phenomena of random fluctuations over time. When I first set forth stochastic differential equations, however, my paper did not attract attention. It was over ten years after my paper that other mathematicians began reading my "musical scores" and playing my "music" with their "instruments."
K. Ito, My Sixty Years in Studies of Probability Theory : acceptance speech of the Kyoto Prize in Basic Sciences (1998). |
:: Cvičenia (2) ::
- Vypočítajte dy, ak
- y(t)=w(t)3
- y(t)=exp(w(t))
- y(t)=exp(2t+5w(t))
- y(t)=ln(x(t)), kde dx(t)=3x(t)dt+6x(t)dw(t)
- Nech cena akcie S vyhovuje stochastickej diferenciálnej rovnici
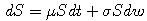
- Ukážte, že jej vývoj sa riadi geometrickým Brownovym pohybom a určte jeho parametre.
- Aká je stredná hodnota ročného výnosu akcie?
- Nech je daná dnešná cena akcie S0 . Aká je stredná hodnota ceny akcie o mesiac?
:: Ďalšie príklady na precvičenie ::
- Nech cena akcie S(t) vyhovuje stochastickej diferenciálnej rovnici
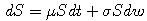 .
Akej rovnici vyhovuje súčasná hodnota e-rtS(t),
kde r je úroková miera (predpokladáme, že je konštantná)?
.
Akej rovnici vyhovuje súčasná hodnota e-rtS(t),
kde r je úroková miera (predpokladáme, že je konštantná)?
- Nech náhodný proces S(t) vyhovuje stochastickej diferenciálnej rovnici
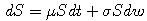 a n je prirodzené číslo. Dokážte, že proces
Sn sa riadi geometrickým Brownovym pohybom.
a n je prirodzené číslo. Dokážte, že proces
Sn sa riadi geometrickým Brownovym pohybom.
- Uvažujme dve akcie. Prvá z nich sa riadi geometrickým Brownovym pohybom S(t)=S(0)*exp(0.2t+0.3w(t)), druhá vyhovuje stochastickej diferenciálnej rovnici dS(t)=0.2dt+0.3dw(t). Ktorá akcia má väčšiu strednú hodnotu ročného výnosu?
- Uvažujme proces
Na obrázku je niekoľko realizácií tohto procesu.

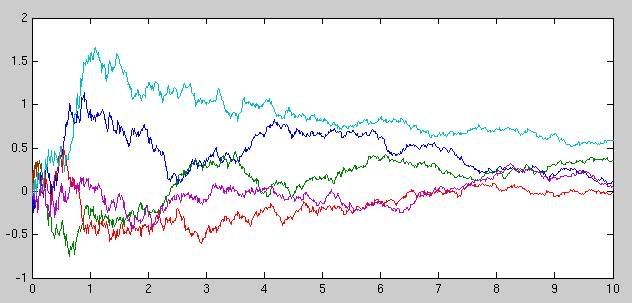
- Vypočítajte strednú hodnotu a disperziu procesu v čase t. V ktorom čase je disperzia maximálna?
- Dokážte, že tento proces vyhovuje stochastickej diferenciálnej rovnici

Beáta Stehlíková (www)
Cvičenia z finančných derivátov, FMFI UK Bratislava, LS 2009/2010