Európske opcie
:: Opakovanie ::
Prvú polhodinu budeme venovať príkladom na precvičenie z prvých dvoch cvičení. Ak máte otázky ku konkrétnym príkladom, budeme riešiť tie. Inak vyberiem niekoľko príkladov, ktoré preriešime.:: Európska call a put opcia ::
- Európska call opcia je kontrakt, v ktorom majiteľ, opcie získava právo (ale nie povinnosť) kúpiť akciu v presne určenom expiračnom čase za vopred dohodnutú expiračnú cenu E.
- Európska put opcia
je kontrakt, v ktorom majiteľ, opcie získava právo (ale nie povinnosť) predať akciu v presne určenom
expiračnom čase za vopred dohodnutú expiračnú cenu E.
- Payoff = hodnota v čase expirácie
- Payoff call opcie:
- Ak aktuálna cena S akcie v čase expirácie prekročí hodnotu E, na ktorú bol uzavretý opčný kontrakt typu call, tak cena opčnej prémie (keby sa za ňu platilo v tomto čase) je zrejme rozdiel medzi aktuálnou cenou S a dohodnutou cenou E, t.j. S-E.
- Na druhej strane, pokiaľ, aktuálna cena akcie neprekročí dohodnutú cenu E, tak opcia nemá žiadnu hodnotu, pretože ju vôbec neuplatníme.
- To znamená, že ocenenie call opcie v čase expirácie je jednoduché: max(S-E,0)
- Analogicky dostaneme payoff put opcie: max(E-S,0)
- Definujeme v Matlabe funkcie, ktoré vrátia payoff call opcie
function [cp]=CallPayoff(S,E) cp=max(S-E,0)
a put opciefunction [pp]=PutPayoff(S,E) pp=max(E-S,0)
Teraz môžeme kresliť payoff diagram a profit diagram (payoff znížený o cenu stratégie).% profit diagram call opcie s E=50 USD, ak jej cena je 5 USD S=0:10:100; plot(s,CallPayoff(s,50)-5);
:: Cvičenia (1) ::
- Predpokladajme, že vlastníme jednu put opciu s expiračnou cenou 60 USD, ktorá stojí 7 USD.
- Nakreslite payoff a profit diagram.
- Pre aké ceny akcie v čase expirácie dosiahneme zisk?
- Aký maximálny zisk môžeme dosiahnuť? Akú maximálnu stratu?
:: Kombinované stratégie ::
Link: http://www.theoptionsguide.com/
- Neutral (non-directional) strategies - používajú sa v
prípade, že investor nevie, ktorým smerom sa cena akcie pohne. Líšia sa
tým, či predpokladáme malú alebo veľkú zmenu ceny akcie (bez
špecifikácie smeru tejto zmeny).
- Ak očakávame malú zmenu ceny, možné stratégie sú napríklad:
- Short straddle: http://www.theoptionsguide.com/short-straddle.aspx
- Short strangle: http://www.theoptionsguide.com/short-strangle.aspx
- Long call condor: http://www.theoptionsguide.com/condor.aspx
- Long call butterfly: http://www.theoptionsguide.com/butterfly-spread.aspx
- Ak očakávame veľkú zmenu ceny, možné stratégie sú napríklad:
- Long straddle: http://www.theoptionsguide.com/long-straddle.aspx
- Long strangle: http://www.theoptionsguide.com/long-strangle.aspx
- Short call condor: http://www.theoptionsguide.com/short-condor.aspx
- Short call butterfly: http://www.theoptionsguide.com/short-butterfly.aspx
- Ak očakávame malú zmenu ceny, možné stratégie sú napríklad:
- Bearish strategies (medvedie stratégie) - založené sú na predpoklade investora, že cena akcie klesne. Príkladmi takýchto stratégií sú:
- Bear call spread: http://www.theoptionsguide.com/bear-call-spread.aspx
- Bear put spread: http://www.theoptionsguide.com/bear-put-spread.aspx
- Bullish strategies (býčie stratégie) - založené sú na predpoklade investora, že cena akcie vzrastie.
Príkladmi takýchto stratégií sú:
- Bull call spread: http://www.theoptionsguide.com/bull-call-spread.aspx
- Bull put spread: http://www.theoptionsguide.com/bull-put-spread.aspx
:: Reálne ceny opcií ::
- http://finance.yahoo.com
- Zadáme kód alebo ho vyhlľadáme podľa názvu:

- Pre zvolemú firmu klikneme na Options (v ľavom stĺpci):

- Ukážka:
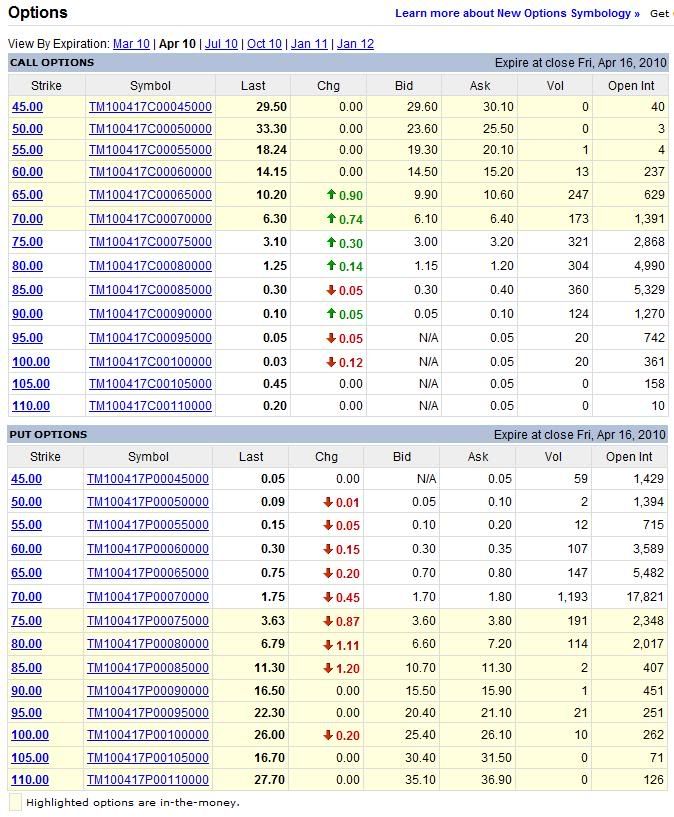
- Opciu môžeme kúpiť za ask, predať za bid.
:: Cvičenia (2) ::
- Zvoľte si kombinovanú stratégiu a pomocou reálnych cien zostrojte jej payoff diagram. Aké presvedčenie o budúcom vývoji akcie vyjadruje takáto stratégia? Pre aké ceny akcie v čase expirácie bude zisková?
:: Obmedzenia na ceny opcií ::
-
Označme c(S,
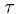 ,E),
p(S,
,E),
p(S,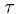 ,E) cenu call, resp. put opcie s expiračnou cenou E, ak aktuálna cena akcie je S a do expirácie opcie zostáva
čas
,E) cenu call, resp. put opcie s expiračnou cenou E, ak aktuálna cena akcie je S a do expirácie opcie zostáva
čas 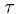 .
.
- Ceny opcií musia vyhovovať určitým nerovnostiam, ktoré
vyplývajú z neprípustnosti arbitráže. Myšlienka ich dôkazu je
nasledovná: Uvažujme dve portfóliá (zložené z akcií, opcií a dlhopisov). Ak v
čase expirácie opcií platí pre hodnoty týchto portfólií nerovnosť
P1
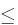 P2, tak rovnaká nerovnosť pre hodnoty portfólií musí platiť aj vo všetkých predchádzajúcich časoch.
P2, tak rovnaká nerovnosť pre hodnoty portfólií musí platiť aj vo všetkých predchádzajúcich časoch.
-
Príklad:
Dokážte, že c(S,
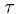 ,E1)
,E1)
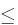 c(S,
c(S,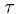 ,E2) pre E2
,E2) pre E2
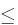 E1
E1
Riešenie: Uvažujme dve portfóliá. V prvom budeme mať opciu s expiračnou cenou E1, v druhom opciu s expiračnou cenou E2. Nerovnosť hovorí, že ak do expirácie opcií zostáva čas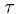 , tak hodnota prvého portfólia je menšia alebo rovná hodnote druhého portfólia. Podľa horeuvedenej úvahy stačí túto nerovnosť dokázať v čase expirácie.
, tak hodnota prvého portfólia je menšia alebo rovná hodnote druhého portfólia. Podľa horeuvedenej úvahy stačí túto nerovnosť dokázať v čase expirácie.
V čase expirácie bude mať prvé portfólio hodnotu max(S-E1,0), druhé portfólio bude mať hodnotu max(S-E2,0).
0 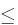 S
S 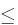 E2
E2
E2 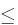 S
S 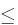 E1
E1
E1 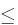 S
S
portfólio 1 0 0 S- E1 portfólio 2 0 S- E2 S- E2 porovnanie 0=0 0 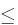 S- E2
S- E2S- E1 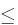 S- E2
S- E2
Vidíme teda, že nerovnosť platí pre ľubovoľné S.
:: Cvičenia (3) ::
- Uvažujme nasledovné ceny call opcií:
Nájdite arbitrážnu príležitosť - teda takú stratégiu, ktorá bez ohľadu na cenu akcie v čase expirácie opcií prinesie zisk. Nakreslite profit diagram vašej stratégie.Expiračná cena Cena call opcie 10 30 15 26 20 27 25 23 30 19 -
Dokážte, že p(S,
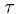 ,E1)
,E1)
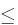 p(S,
p(S,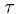 ,E2) pre E1
,E2) pre E1
 E2
a zostavte príklad arbitrážnej príležitosti, ak táto nerovnosť neplatí (s konkrétnymi číslami, tak ako v predchádzajúcom cvičení).
E2
a zostavte príklad arbitrážnej príležitosti, ak táto nerovnosť neplatí (s konkrétnymi číslami, tak ako v predchádzajúcom cvičení).
:: Ďalie príklady na precvičenie ::
-
[Vzorová písomka, 2008]

-
[Písomka, 2009]
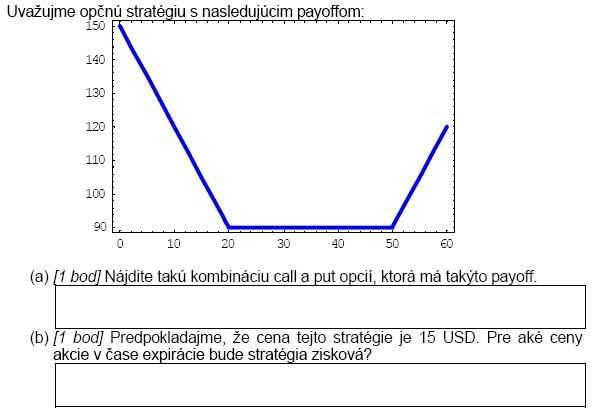
-
[Rüdiger U. Seydel: Tools for Computational Finance.]

- Dokážte:
-
S - E exp(-r
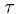 )
)
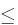 c(S,
c(S,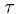 ,E)
,E)
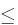 S,
kde r je úroková miera.
S,
kde r je úroková miera. -
Funkcia c(S,
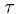 ,E)
je konvexnou funkciou expiračnej ceny E
,E)
je konvexnou funkciou expiračnej ceny E
-
Funkcia p(S,
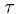 ,E)
je konvexnou funkciou expiračnej ceny E
,E)
je konvexnou funkciou expiračnej ceny E
-
S - E exp(-r
-
[Vzorová písomka, 2009]
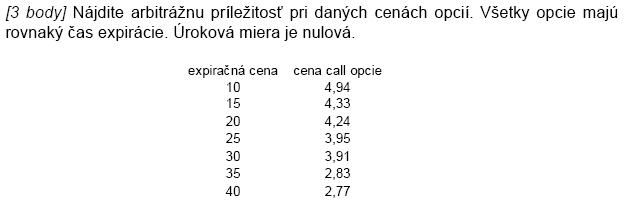
-
[Písomka, 2009]

Beáta Stehlíková (www)
Cvičenia z finančných derivátov, FMFI UK Bratislava, LS 2009/2010