Lelandov model (zahrnutie transakčných nákladov)
:: Lelandov model (zahrnutie transakčných nákladov) ::
- Lelandov model (Hayne E. Leland: Option Pricing and Replication with Transactions Costs, 1985)
- Bid a ask cena akcie: Sbid, Sask - definujeme
- S=(Sbid + Sask)/2
- c=(Sask - Sbid)/S
- Transakčné náklady na jednu transakciu: (c/2)S
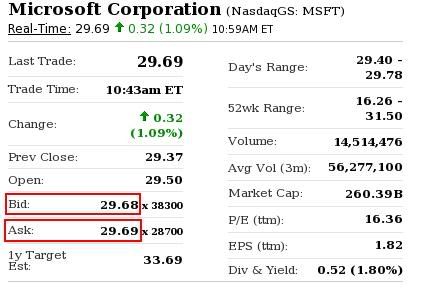
- Aké by malo byť c? Zrátajme si na ukážku, čomu sa rovná pre tieto akcie: (Ide o bid a ask ceny iba v jednom konkrétnom okamihu, pre presnejší odhad by sme potrebovali viac dát.)


- PDR pre ceny derivátov:
- Replikačné portfólio v Black-Scholesovom modeli: 1 opcia,
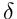 , akcií spojité obchodovanie.
, akcií spojité obchodovanie.
- V prípade transakčných nákladov: 1 opcia,
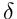 akcií, portfólio meníme v intervaloch dĺžky
akcií, portfólio meníme v intervaloch dĺžky 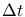 , počet transakcií je
, počet transakcií je 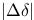
- Zmena hodnoty portfólia:

- Na cvičení odvodíme rovnicu:
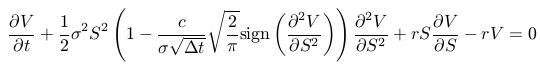
- Replikačné portfólio v Black-Scholesovom modeli: 1 opcia,
- Pre call a put opciu:
- Definujeme Lelandovo číslo

- Pre Lelandovo číslo z intervalu (0,1) dostávame cenu call,
resp. put opcie pomocou Black-Scholesovho vzorca s upravenou
volatilitou:
Dôkaz: dosadíme do rovnice, využujeme, že cena call a put opcie v Black-Scholesovom modeli je konvexná funkcia premennej S.
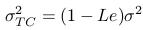
- Definujeme Lelandovo číslo
:: Cvičenia (1) ::
- Dokážte, že prítomnosť transakčných nákladov znižuje cenu opcie.
- Napíšte funkciu, ktorá počíta hodnotu Lelandovho čísla (v závislosti of volatility akcie, konštanty c, intervalu medzi dvoma zaisteniami portfólia). Napíšte funkciu, ktorá overí podmienku, že Lelandovo číslo je z intervalu (0,1). Ak je splnená, vypočíta hodnotu call a put opcie za prítomnosti transakčných nákladov (parametre: cena akcie, expiračná cena, volatilita, čas do expirácie, úroková miera, konštanta c, interval medzi dvoma zaisteniami portfólia).
- Zvoľte si parametre akcie a opcie, a úrokovú mieru - vstupy potrebné do Lelandovho modelu. Aké časy medzi dvoma zmenami portfólia sú prípustné? Pre jeden z nich vypočítajte cenu opcie a porovnajte ju s Black-Scholesovou cenou.
:: Modelovanie bid-ask spreadov pomocou Lelandovho modelu ::
- Cenu z predchádzajúceho odvodenia môžeme považovať za ponuku na kúpu opcie.
- Ak chceme odvodiť ponuku na predaj, uvažujeme portfólio, v ktorom dlhujeme jednu opciu. Toto portfólio hedžujeme. Rovnakým postupom dostaneme:
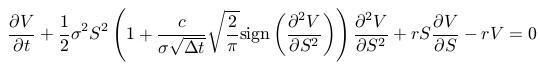
- Cenu call, resp. put opcie znovu dostaneme pomocou Black-Scholesovho vzorca, pričom upravená volatilita je:
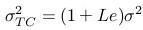
- To znamená, že upravené volatility sú:
a rozdiel medzi ask a bid cenou je
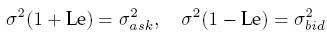
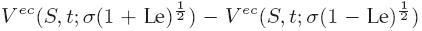
- Tieto výsledky nám umožňujú odhadnúť parametre modelu z dát:
- Vypočítame implikované bid a ask volatility
 a
a 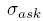 z bid a ask ceny opcie:
z bid a ask ceny opcie:
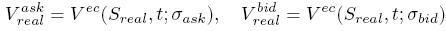
- Riešením sústavy rovníc vypočítame parametre
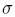 (implikovaná volatilita), Le:
(implikovaná volatilita), Le:
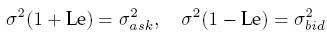
- Z bid a ask ceny akcie vypočítame konštantu c z Lelandovho modelu.
- Nakoniec vypočítame implikovaný čas medzi dvoma prerovnaniami porfólia pri hedžingu opcie:
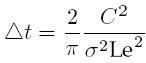
- Vypočítame implikované bid a ask volatility
:: Cvičenia (2) ::
-
Použite uvedený postup na odhad parametrov Lelandovho modelu pomocou niektorej z nasledovných call opcií (dáta sú zo 17. marca 2010):


:: Poznámky ::
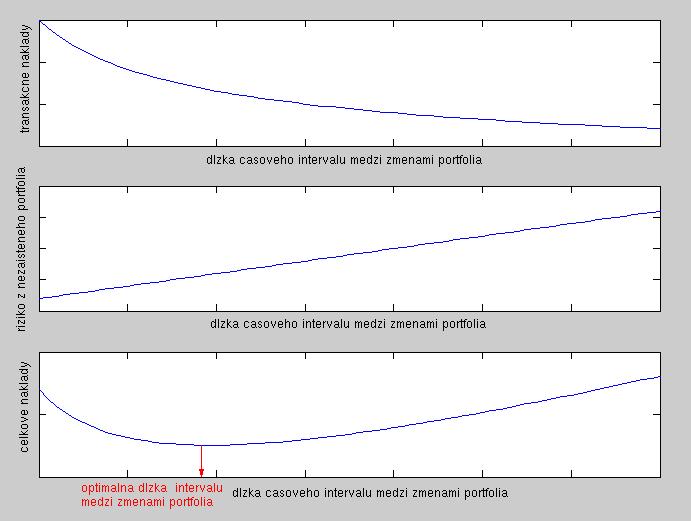
- Ako voliť dĺžku intervalu medzi dvoma nasledujúcimi zmenami portfólia? Existujú modely (RAPM - Risk Adjusted Pricing Methodology), ktoré berú do úvahy dve veci:
- transakčné náklady - tie sa klesajú, keď rastie dĺžka časového intervalu medzi dvoma nasledujúcimi zmenami portfólia
- riziko z nezabezpečeného portfólia - ak rastie dĺžka tohto časového intervalu, vzniká stále väčšie riziko z výkyvov cien na trhu, keďže naše portfólio sa vzďaľuje od replikačného portfólia zo spojitého modelu
-
Rovnica na oceňoavanie derivátov v Lelandovom modeli s transakčnými nákladmi
nie je lineárna. To znamená, že napríklad súčet, rozdiel, alebo nejaká iná kombinácia riešení už nie je riešením. Z toho vyplýva, že cena kombinovaných stratégií sa už nedá vypočítať tak, že oceníme každú opciu zvlášť a výsledok zložíme. (To sa dá len pri lineárnych rovniciach, ako je napríklad pôvodná Black-Scholesova rovnica.) Nemožnosť takéhoto výpočtu sa dá vidieť aj z nasledovnej úvahy:
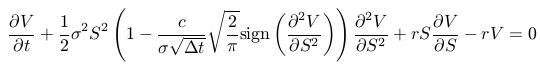
Ak oceníme každú opciu samostatne, zarátavame tak transakčné náklady vznikajúce z udržiavania každého replikačného portfólia zvlášť. Ak nemáme transakčné náklady, nevadí, že udržiavame akoby dve replikačné portfóliá. Môže sa stať, že v jednom akcie kupujeme a v druhom predávame. Žiadne náklady z toho však nevznikajú. V prípade transakčných nákladov to už nie je pravda. Vtedy treba portfólio uvažovať ako celok, a v prípade uvedenej situácie nerobiť zbytočné transakcie.
:: Ďalšie príklady na precvičenie ::
- [Vzorová písomka, 2009]

- [Písomka, 2009]
Poznámka: Teraz sme na cvičení pracovali s opciami firmy AMZN, takže pri riešení tejto úlohy si vyberte niektorú z týchto put opcií.

- Uvažujme rozdiel bid a ask ceny opcie ako funkciu ceny akcie S. (Ostatné parametre - volatilita akcie, parameter c charakterizujúci transakčné náklady, úroková miera, expiračná cena a čas expirácie opcie - sú konštantné).
- Znazornite graficky tento rozdiel pre zvolené hodnoty parametrov.
- Pre akú cenu akcie je tento rozdiel maximálny? Vypočítajte analyticky pre všeobecné hodnoty parametrov.
Beáta Stehlíková (www)
Cvičenia z finančných derivátov, FMFI UK Bratislava, LS 2009/2010