Numerické riešenie Black-Scholesovej PDR (II.)
:: Konvergencia Gauss-Seidelovej metódy ::
- Na výpočet riešenia sústavy lineárnych rovníc sme použili Gauss-Seidelovu metódu.
- Ak je matica sústavy diagonálne dominantná, Gauss-Seidelova metóda konverguje k riešeniu pre ľubovoľný štartovací bod.
- Vidíme, že matica z našej úlohy je diagonálne dominantná.
:: Rýchlosť konvergencie metódy ::
- Najskôr si pripomeňme, čo je to spektrálny polomer matice a ako súvisí s maticovými normami:
- Spektrálny polomer je maximum z absolútnych hodnôt vlastných čísel matice:
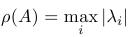
- Pre maticovú normu platí:
Túto vlastnosť si numericky vyskúšame v Matlabe:
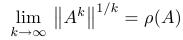
- Maticové normy v Matlabe:

- Pre maticu, ktorú si vytvoríme - napríklad náhodnú:
teda vieme vypočítať spektrálny polomer
a počítať normy jej mocnín. Pre 1-normu dostaneme:

- Zopakujte pre inú maticu a/alebo inú normu.
- Maticové normy v Matlabe:
- Pre k veľké teda máme:
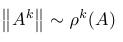
- Spektrálny polomer je maximum z absolútnych hodnôt vlastných čísel matice:
- Vrátime sa teraz k metódam riešenia sústavy rovníc. Metódu zapíšeme v tvare
a budeme počítať vzdialenosť n-tej iterácie od presného riešenia:
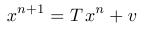 Spektrálny polomer matice T by teda mal byť menší ako 1 a čo najbližšie k nule.
Spektrálny polomer matice T by teda mal byť menší ako 1 a čo najbližšie k nule.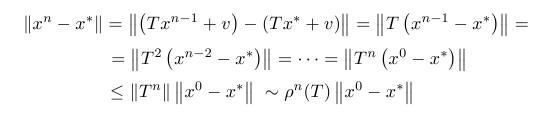
:: SOR (successive over relaxation) metóda
- Ako urýchliť konvergenciu Gauss-Seidelovej metódy?
- Modifikáciou Gauss-Seidelovej metódy je SOR (successive over relaxation) metóda:
Pre

 =1, dostávame pôvodnú Gauss-Seidelovu metódu,
=1, dostávame pôvodnú Gauss-Seidelovu metódu,  > 1 - over-relaxation,
> 1 - over-relaxation,  < 1 - under-relaxation.
< 1 - under-relaxation.
-
Bez dôkazu uvedieme nasledovné tvrdenia týkajúce sa konvergencie tejto metódy:
- Nutnou podmienkou na to, aby SOR metóda konvergovala, je, že parameter
 je z intervalu (0,2)
je z intervalu (0,2)
- Pre sústavu, ktorú riešime pri numerickom riešení B-S rovnice, konverguje SOR metóda pre ľubovoľné
 z intervalu (0,2).
z intervalu (0,2).
- Nutnou podmienkou na to, aby SOR metóda konvergovala, je, že parameter
- Ak túto maticu rozložíme na jej dolnú trojuholníkovú časť (L), hornú (U) a diagonálnu (D), tak SOR metódu môžeme napísať v tvare
kde
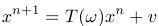 Optimálna voľba parametra
Optimálna voľba parametra
 teda závisí od spektrálneho polometru matice T. Ten závisí od parametrov modelu a delenia, ktoré sme použili.
teda závisí od spektrálneho polometru matice T. Ten závisí od parametrov modelu a delenia, ktoré sme použili.
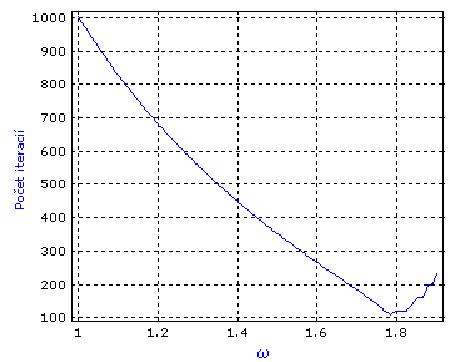
Ukážka:
- spektrálny polomer matice T v závislosti od parametra
 :
:

- počet iterácií potrebný na výpočet riešenia na jednej časovej vrstve:
- čas výpočtu v sekundách:
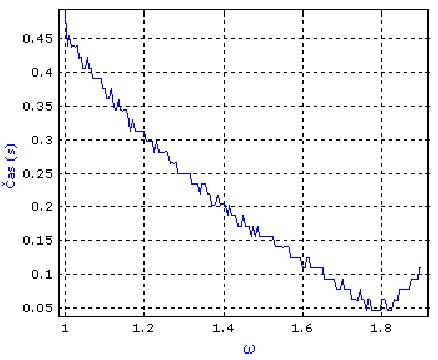
 , by nebolo efektívne. Takéto grafy nám však dávajú predstavu o tom, ako tento parameter vplýva na konvergenciu. Prakticky zvolíme hodnotu zhruba medzi 1.5 a 1.9.
, by nebolo efektívne. Takéto grafy nám však dávajú predstavu o tom, ako tento parameter vplýva na konvergenciu. Prakticky zvolíme hodnotu zhruba medzi 1.5 a 1.9.
- spektrálny polomer matice T v závislosti od parametra
:: Cvičenie ::
Upravte funkciu gs.m tak, aby počítala zadanú sústavu SOR metňodou so zadaným parametrom . :
:
Použite ju na výpočet numerického riešenia ceny call opcie - hlavný program zostáva rovnaký, jediná zmena je, že namiesto funkcie gs voláte funkciu sor.
:: Ďalšie úlohy na precvičenie ::
- Naprogramujte numerický výpočet ceny put opcie. (Okrajové podmienky: ak je cena akcie S blízka nule, cena put opcie je približne E*exp(-r*tau)-S*exp(-D*tau), ak je cena akcie veľmi veľká, cena put opcie je blízka nule.)
-

Mali by ste dostať podobné grafy ako sú vyššie na tejto stránke.
Beáta Stehlíková (www)
Cvičenia z finančných derivátov, FMFI UK Bratislava, LS 2009/2010