Náhodné procesy, modelovanie cien akcií
:: Stochastický vývoj finančných veličín ::
-
Z priebehov cien akcií (ako aj iných finančných veličín - úrokových mier, výmenných kurzov, ...) vidíme, že ich priebeh sa nedá popísať deterministickou funkciou. Preto sa na ich modelovanie používajú náhodné procesy.
-
Vľavo: trend (vývoj ceny počas piatich rokov), vpravo: fluktuácie (vývoj ceny počas niekoľkých hodín):
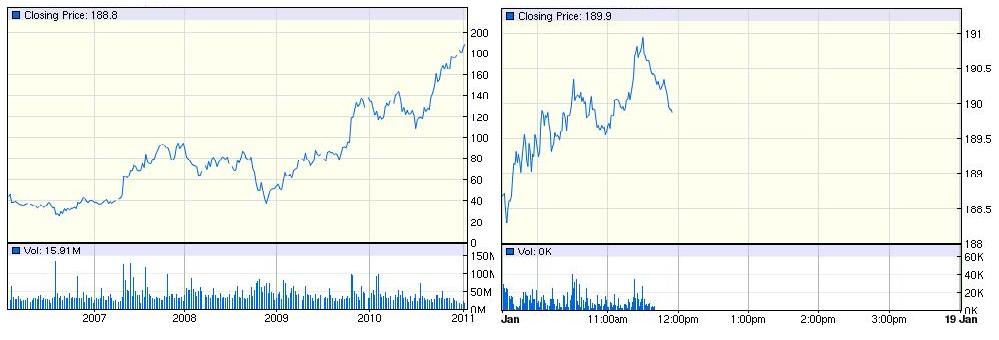 Zdroj: http://finance.google.com
Zdroj: http://finance.google.com
:: Wienerov proces a Brownov pohyb ::
-
Základným náhodným procesom, z ktorého sú ostatné odvodené, je Wienerov proces. Pripomeňme si jeho definíciu:
Náhodný proces {W(t), tĎalej bude w všade označovať Wienerov proces.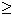 0} sa nazýva Wienerov proces, ak
0} sa nazýva Wienerov proces, ak
- prírastky
W(t+
 ) - W(t)
majú normálne rozdelenie s nulovou strednou hodnotou a s disperziou
) - W(t)
majú normálne rozdelenie s nulovou strednou hodnotou a s disperziou  ,
,
- pre každé delenie 0 = t0
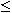 t1
t1 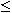 ...
... 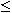 tn sú prírastky
Wti+1 - Wti nezávislé náhodné premenné s parametrami podľa predchádzajúceho bodu,
tn sú prírastky
Wti+1 - Wti nezávislé náhodné premenné s parametrami podľa predchádzajúceho bodu,
- W(0)=0,
- trajektórie sú spojité.
- prírastky
W(t+
-
Ako získame realizáciu Wienerovho procesu?
- Budeme generovať aproximáciu - hodnoty v diskrétnych bodoch typu (čas, hodnota), ktoré pospájame.
- Hodnoty budú v bodoch 0,
 ,2
,2 , . . ., kde
, . . ., kde  je dostatočne malý časový krok.
je dostatočne malý časový krok.
- Hodnota v čase 0 je 0.
- Prírastok na intervale [k
 , (k + 1)
, (k + 1) ] je náhodná premenná s nulovou strednou hodnotou
a varianciou
] je náhodná premenná s nulovou strednou hodnotou
a varianciou  .
.
V Matlabe:
%------------------------------- % SIMULACIA WIENEROVHO PROCESU %------------------------------- T=1; % do casu T dt=0.001; % casovy krok dt t=(0:dt:T); % vektor casov, v ktorych generujeme hodnoty procesu n=length(t); w(1)=0; % Wienerov proces zacina z nuly for i=1:n-1 % prvu hodnotu mame, potrebujeme zvysnych n-1 dw=sqrt(dt)*randn; % prirastok dw; randn ~ N(0,1) => dw ~ N(0,dt) w(i+1)=w(i)+dw; % nova hodnota = povodna + prirastok end; plot(t,w); % vykreslime priebeh
Poznamenajme, že na zrýchlenie výpočtov v Matlabe sa dajú využiť funkcie pre prácu s vektormi (namiesto cyklov):
%------------------------------------------- % RYCHLEJSIA SIMULACIA WIENEROVHO PROCESU %------------------------------------------- T=1; % do casu T dt=0.001; % casovy krok dt t=(0:dt:T); % vektor casov, v ktorych generujeme hodnoty procesu n=length(t); dw=sqrt(dt)*randn(n-1,1); % vektor prirastkov - nezavisle N(0,dt) w=[0;cumsum(dw)]; % zaciname z nuly, dalej kumulativne sucty dw plot(t,w); % vykreslime priebeh
Ukážka výstupu: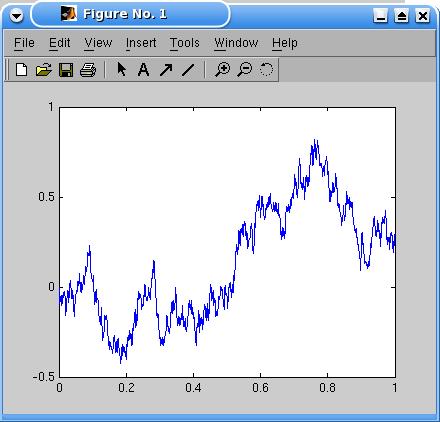
-
Ak k násobku Wienerovho procesu pridáme lineárny trend:
dostávame proces, ktorý sa nazýva Brownov pohyb.
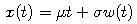
Ak je parameter
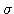 nulový, grafom je priamka. Pre nenulovú hodnotu
nulový, grafom je priamka. Pre nenulovú hodnotu 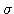 sa k tomuto lineárnemu trendu pridávajú náhodné fluktuácie.
sa k tomuto lineárnemu trendu pridávajú náhodné fluktuácie.
:: Cvičenia (1) ::
-
Nakreslite do jedného grafu niekoľko realizácií Wienerovho procesu.
Ukážka výstupu: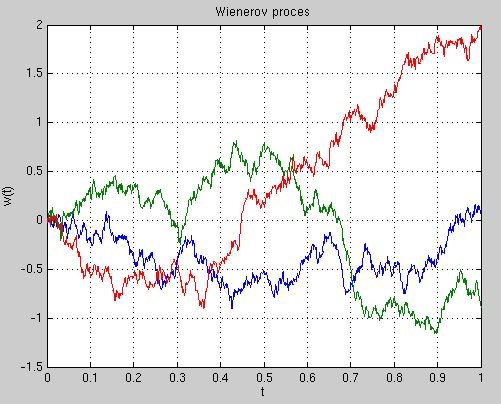
-
Nakreslite do jedného grafu niekoľko realizácií Brownovho pohybu so zvolenými parametrami. Do toho istého grafu zakreslite strednú hodnotu tohto procesu.
Ukážka výstupu: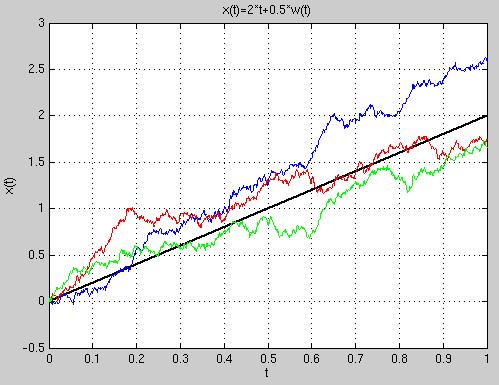
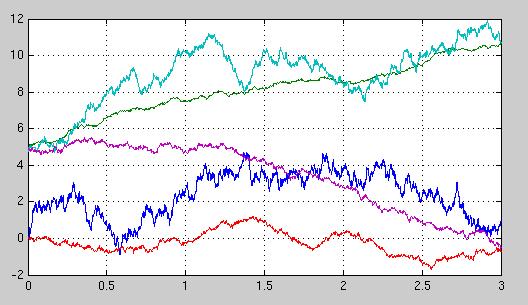
- Priraďte procesy
- x1(t)=w(t)
- x2(t)=3*w(t)
- x3(t)=5+2*t+w(t)
- x4(t)=5+2*t+0.5*w(t)
- x5(t)=5-3*t+w(t)
- Definujme proces m(t)=max(w(s), s
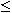 t), t. j. maximum Wienerovho procesu na intervale [0,t]. Zobrazte do jedného grafu trajektóriu Wienerovho procesu a trajektóriu procesu m(t) (počítaného z tejto realizácie Wienerovho procesu).
t), t. j. maximum Wienerovho procesu na intervale [0,t]. Zobrazte do jedného grafu trajektóriu Wienerovho procesu a trajektóriu procesu m(t) (počítaného z tejto realizácie Wienerovho procesu).
Ukážka výstupu: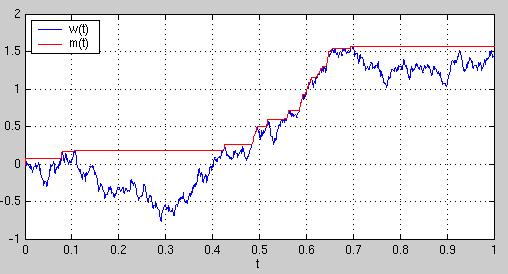
:: Geometrický Brownov pohyb ::
-
Geometrický Brownov pohyb je proces definovaný vzťahom
pričom x0 predstavuje hodnotu procesu v čase 0.
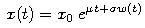
-
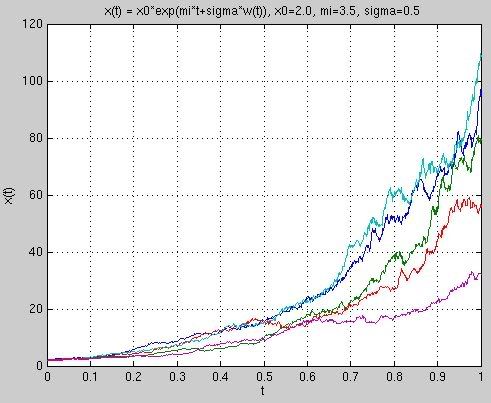
Ukážka trajektórií geometrického Brownovho pohybu:
:: Modelovanie cien akcií pomocou geometrického Brownovho pohybu ::
-
Cenu akcie S modelujeme geometrickým Brownovym pohybom:
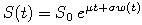
-
Na výpočet výnosov sa používa veličina
pričom posledná aproximácia vyplýva z toho, že
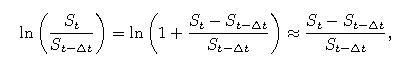
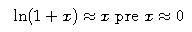
-
Ak sa cena akcie S riadi geometrickým Brownovym pohybom, tak pre výnosy dostávame
teda výnosy sú nezávislé náhodné premenné s normálnym rozdelením a uvedenými parametrami.
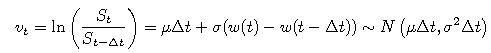
- Ako získať parametre geometrického Brownovho pohybu z dát - odhadom parametrov normálneho rozdelenia z výnosov:
- Zo súboru goog.txt načítame dáta do Matlabu.
Ide o denné dáta cien akcie firmy Google v rokoch 2009 a 2010, na začiatku súboru sú najstaršie dáta.
s=load('goog.txt'); dt=1/252; % denne data, cas sa v modeli pocita v rokochPriebeh ceny je nasledovný: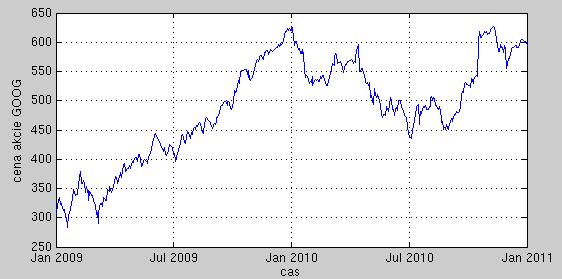
- Definujeme výnosy - napríklad takto:
n=length(s); for i=1:n-1 v(i)=log(s(i+1)/s(i)); end; % alebo vektorovo namiesto cyklu: % v=log(s(2:n)./s(1:n-1));
- Vieme, že tieto výnosy majú normálne rozdelenie. Ďalej vieme, že strednú hodnotu normálneho rozdelenia odhadujeme aritmetickým priemerom a disperziu výberovou disperziou. Vypočítame teda priemer a výberovú disperziu vektora v - budú to odhady veličín
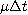 a
a 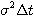
miDelta=mean(v); % odhad mi*dt s2Delta=var(v); % odhad (sigma^2)*dt
- Nakoniec vypočítame odhady samotných parametrov
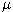 a
a 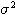 :
:
mi=miDelta/dt; % odhad parametra mi sigma=sqrt(s2Delta/dt); % odhad parametra sigma
- Dostaneme:
>> mi mi = 0.3225 >> sigma sigma = 0.2877
- Zo súboru goog.txt načítame dáta do Matlabu.
Ide o denné dáta cien akcie firmy Google v rokoch 2009 a 2010, na začiatku súboru sú najstaršie dáta.
:: Black-Scholesov model a Monte Carlo simulácie ::
- Z finančnej matematiky poznáte Black-Scholesov model a oceňovanie derivátov pomocou rizikovo neutrálnej pravdepodobnosti a strednej hodnoty:
- Predpokladajme, že cena akcie S sa vyvíja podľa geometricého Brownovho pohybu
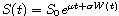 a že derivát má v čase expirácie T hodnotu
a že derivát má v čase expirácie T hodnotu 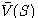 .
.
- Treba si uvedomiť, že dnešná cena derivátu nie je stredná hodnota
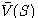 (resp. odúročená stredná hodnota, ak úroková miera nie je nulová). Derivát nie je jednoduchá "stávka", v ktorej dostaneme
(resp. odúročená stredná hodnota, ak úroková miera nie je nulová). Derivát nie je jednoduchá "stávka", v ktorej dostaneme 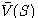 , pričom S má určité pravdepodobnostné rozdelenie. Máme totiž možnosť obchodovať aj so samotnou akciou.
, pričom S má určité pravdepodobnostné rozdelenie. Máme totiž možnosť obchodovať aj so samotnou akciou.
- Dá sa dokázať, že cena derivátu je odúročená stredná hodnota, ale pri inej - tzv. rizikovo neutrálnej - pravdepodobnostnej miere. Cena akcie sa aj pri tejto pravdepodobnosti riadi geometrickým Brownovym pohybom, ale namiesto driftu
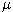 máme
máme
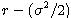 , kde r je bezriziková úroková miera. Volatilita
, kde r je bezriziková úroková miera. Volatilita 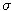 zostáva rovnaká.
zostáva rovnaká.
- To znamená, že pre cenu
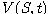 platí:
kde Q je spomínaná rizikovo neutrálna miera.
platí:
kde Q je spomínaná rizikovo neutrálna miera.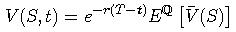
- Predpokladajme, že cena akcie S sa vyvíja podľa geometricého Brownovho pohybu
- Vieme, že strednú hodnotu náhodnej premennej môžeme aproximovať aritmetickým priemerov jej realizácií. Ak teda spravíme N simulácií vývoja ceny akcie a označíme Si cenu akcie v čase expirácie v i-tej simulácii, tak môžeme aproximovať strednú hodnotu
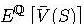 :
a takisto cenu derivatu:
:
a takisto cenu derivatu: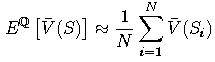 Táto aproximácia konverguje k presnej cene derivátu, ak N ide do nekonečna.
Táto aproximácia konverguje k presnej cene derivátu, ak N ide do nekonečna.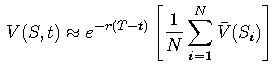
- Vyskúšajme si to na príklade európskej call opcie.
- Zadajme parametre akcie a opcie, ktorú budeme oceňovať:
% PARAMETRE mi=0.35; % parameter z geom. BP sigma=0.30; % parameter z geom. BP s0=150; % aktualna cena akcie E=175; % expiracna cena opcie tau=1/2; % tau = T-t = cas do expiracie, t.j. pol roka r=0.01 % bezrizikova urokova miera, t.j. 1 percento
- V čase expirácie teda máme:
Z=randn; % N(0,1) wT=sqrt(tau)*Z; % Wienerov proces v case T % v RN miere, preto "r-0.5*sigma^2" namiesto "mi" sT=s0*exp((r-0.5*sigma^2)*tau+sigma*wT); % akcia v case T vT=max(0,sT-E); % opcia v case T
- Toto budeme opakovať v cykle a budeme počítať priebežnú hodnotu aproximácie ceny opcie:
N=10000; % pocet simulacii sum=0; % pomocna premenna na vypocet priemeru for i=1:N % ------------------------- % z predchadzajuceho bodu: Z=randn; wT=sqrt(tau)*Z; sT=s0*exp((r-0.5*sigma^2)*tau+sigma*wT); vT=max(0,sT-E); % ------------------------- sum=sum+vT; priemer=sum/i; % priemer z prvych i hodnot cena(i)=exp(-r*tau)*priemer; % aprox. na zaklade prvych i hodnot end;
- Na oceňovanie európskej call opcie je známy explicitný vzorec, získané aproximácie teda môžeme porovnať s presnou hodnotou. Cena tejto konkrétnej call opcie je 4,8572 USD.
plot(cena); hold on; vPresne=4.8572; plot(vPresne*ones(1,N),'r');
Ukážka výstupu: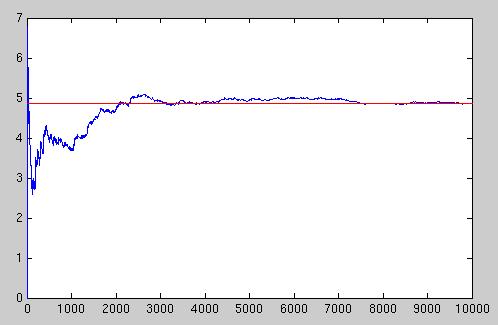
- Zadajme parametre akcie a opcie, ktorú budeme oceňovať:
:: Cvičenie (2) ::
- Zopakujte simulácie viackrát a zakreslite ich do jedného grafu.
Ukážka výstupu (zmenšili sme interval zobrazený na y-ovej osi, aby vynikla konvergencia, a nie veľké odchýlky na začiatku):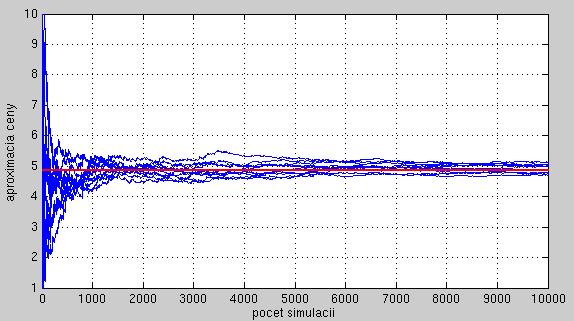
- Ako presné sú hodnoty získané z 10000 simulácií? Nakreslite ich histogram.
Ukážka výstupu (200x sme zopakovali výpočet s N=10000):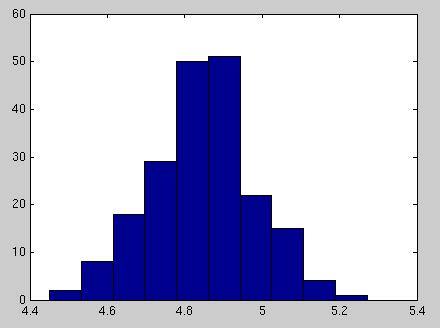
Vyskúšajte pre iné N.
Existujú metódy na zmenšenie variancie odhadu ceny pomocou simulácií. Jednoduchý úvod do týchto metód je v knihe [R. Seydel: Tools for computational finance. Springer 2006] v kapitole 3.5.4 - Variance reduction. Podrobnejšie sa touto témou zaoberá kniha [P. Glassermann: Monte Carlo Methods in Financial Engineering. Springer, 2004] v kapitole 4 (Variance reduction techniques).
:: Ďalšie príklady na precvičenie ::
- Prírastky a ich rozdelenie
-
Definujme proces {Y(t), t
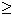 0}, ktorého prírastky
Y(t+
0}, ktorého prírastky
Y(t+ ) - Y(t)
majú strednú hodnotu (
) - Y(t)
majú strednú hodnotu ( )2 a disperziu
)2 a disperziu  .
Ďalej od procesu Y(t) požadujeme, aby pre každé delenie 0 = t0
.
Ďalej od procesu Y(t) požadujeme, aby pre každé delenie 0 = t0 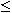 t1
t1 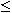 ...
... 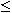 tn boli prírastky
Yti+1 - Yti nezávislé náhodné premenné.
Ukážte, že tieto predpoklady vedú k sporu, t. j. takýto proces neexistuje.
tn boli prírastky
Yti+1 - Yti nezávislé náhodné premenné.
Ukážte, že tieto predpoklady vedú k sporu, t. j. takýto proces neexistuje.
-
Definujme proces {Y(t), t
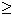 0}, ktorého prírastky
Y(t+
0}, ktorého prírastky
Y(t+ ) - Y(t)
majú nulovú strednú hodnotu a konštantnú nenulovú disperziu.
Ďalej od procesu Y(t) požadujeme, aby pre každé delenie 0 = t0
) - Y(t)
majú nulovú strednú hodnotu a konštantnú nenulovú disperziu.
Ďalej od procesu Y(t) požadujeme, aby pre každé delenie 0 = t0 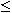 t1
t1 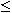 ...
... 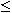 tn boli prírastky
Yti+1 - Yti nezávislé náhodné premenné.
Ukážte, že tieto predpoklady vedú k sporu, t. j. takýto proces neexistuje.
tn boli prírastky
Yti+1 - Yti nezávislé náhodné premenné.
Ukážte, že tieto predpoklady vedú k sporu, t. j. takýto proces neexistuje.
-
Definujme proces {Y(t), t
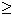 0}, ktorého prírastky
Y(t+
0}, ktorého prírastky
Y(t+ ) - Y(t)
majú nulovú strednú hodnotou a disperziu (
) - Y(t)
majú nulovú strednú hodnotou a disperziu ( )2.
Ďalej od procesu Y(t) požadujeme, aby pre každé delenie 0 = t0
)2.
Ďalej od procesu Y(t) požadujeme, aby pre každé delenie 0 = t0 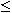 t1
t1 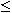 ...
... 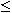 tn boli prírastky
Yti+1 - Yti nezávislé náhodné premenné.
Ukážte, že tieto predpoklady vedú k sporu, t. j. takýto proces neexistuje.
tn boli prírastky
Yti+1 - Yti nezávislé náhodné premenné.
Ukážte, že tieto predpoklady vedú k sporu, t. j. takýto proces neexistuje.
Návod: Prednáška, slajdy Additive property of the Brownian motion - mean a Additive property of the Brownian motion - variance.
-
Definujme proces {Y(t), t
-
Z prednášky:
Spravíme podobný obrázok pre varianciu a tiež pre strednú hodnotu:
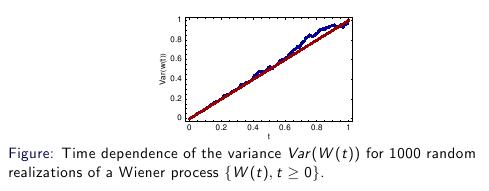
- Zvoľte si delenie intervalu [0,1] a vytvorte maticu, v ktorej budú hodnoty 1000 trajektórií Wienerovho procesu v týchto bodoch.
Ukážka výstupu:
- Vypočítajte výberový priemer a disperziu trajektórií v každom čase a zakreslite ich do grafu spolu s presnými hodnotami strednej hodnoty a disperzie.
Ukážka výstupu: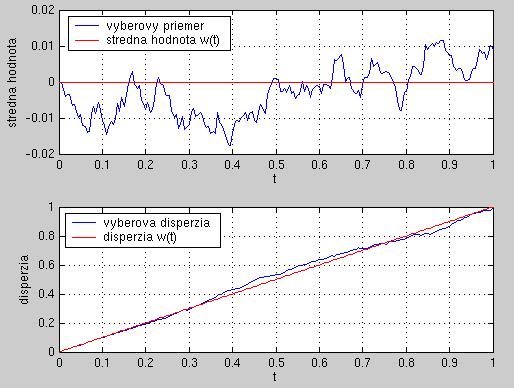
- Zvoľte si delenie intervalu [0,1] a vytvorte maticu, v ktorej budú hodnoty 1000 trajektórií Wienerovho procesu v týchto bodoch.
- Označme tM čas, v ktorom nadobudol Wienerov proces maximum na časovom intervale [0,1]:
Spravte simulácie a zobrazte histogram náhodnej premennej tM.
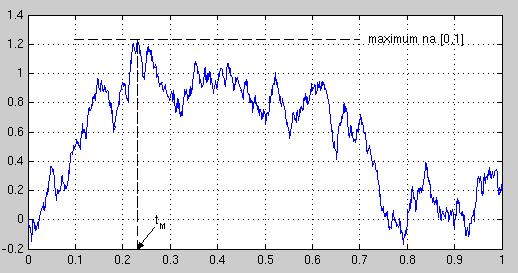
Ukážka výstupu: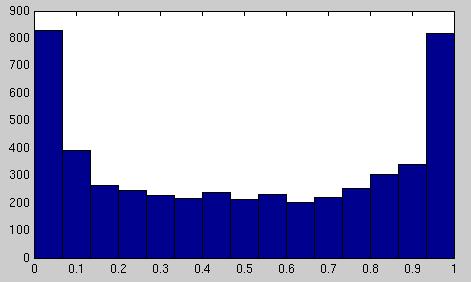
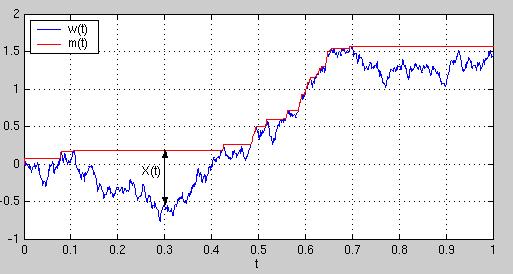
- V cvičení (1)/4 sme definovali proces m, najvyššiu hodnotu Wienerovho procesu, ktorú doteraz dosiahol. Definujte teraz proces X, ktorý vyjadruje vzdialenosť aktuálnej hodnoty Wienerovho procesu od doteraz dosiahnutého maxima:
Doplňte do takéhoto grafu priebeh procesu X.
- Pripomeňme si definíciu a základné vlastnosti lognormálneho rozdelenia:
- Náhodná premenná X má lognormálne rozdelenie, ak jej logaritmus ln(X) má normálne rozdelenie
 .
.
- Hustota náhodnej premennej X s lognormálnym rozdelením je
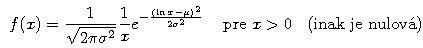
- Stredná hodnota a disperzia náhodnej premennej X s lognormálnym rozdelením je

Predpokladajme, že cena akcie sa riadi geometrickým Brownovym pohybom s parametrami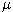 = 0.30,
= 0.30,
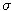 = 0.25
a že dnešná cena akcie je 150 USD.
= 0.25
a že dnešná cena akcie je 150 USD.
- Nakreslite hustotu rozdelenia ceny akcie o mesiac. Ako konrolu porovnajte s histogramom vygenerovaných hodnôt ceny akcie v tomto čase.
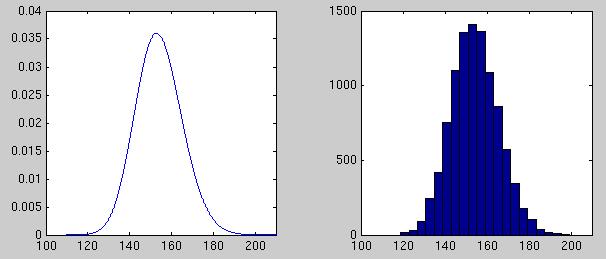
- Aká je pravdepodobnosť, že o mesiac bude cena akcie menšia ako 140 USD?
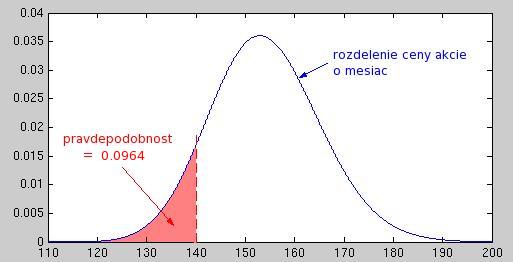
- Nakreslite hustotu rozdelenia štvrťročného výnosu. Aká je stredná hodnota tohto výnosu? Aká je pravdepodobnosť, že bude záporný?
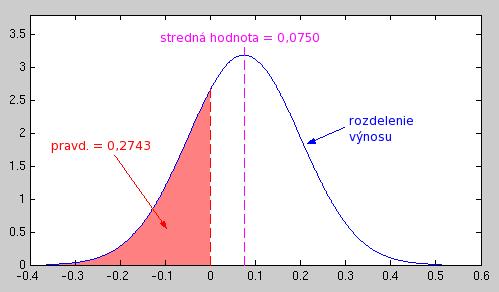
- Náhodná premenná X má lognormálne rozdelenie, ak jej logaritmus ln(X) má normálne rozdelenie
- Čo si myslíte, čo je na obrázku na obale tejto knihy?
Vytvorte podobný obrázok.
Cvičenia z finančných derivátov, 2011
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/
