Citlivosť na parametre - greeks
:: Greeks ::
-
Greeks - derivácie ceny opcie podľa jednotlivých parametrov:
- delta - derivácia podľa ceny akcie
- gama - druhá derivácia podľa ceny akcie
- vega - derivácia podľa volatility
- theta - derivácia podľa času (t.j. mínus derivácia podľa času zostávajúceho do expirácie)
- rho - derivácia podľa úrokovej miery
- Derivácie pre call opciu:
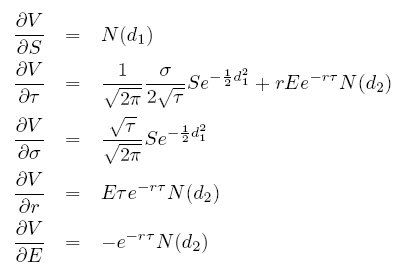
-
Niektorými sme sa už zaoberali:
- delta - derivácia podľa ceny akcie dokazujúca rastúcou ceny call opcie ako funkcie ceny akcie, počet akcií v portfóliu pri hedžovaní jednej vypísanej opcie
- vega - tvrdením, že cena opcie je rastúcou funkciou volatility (pri téme implikovaná volatilita) sme vlastne hovorili, že vega opcie je kladná
:: Cvičenia (1) ::
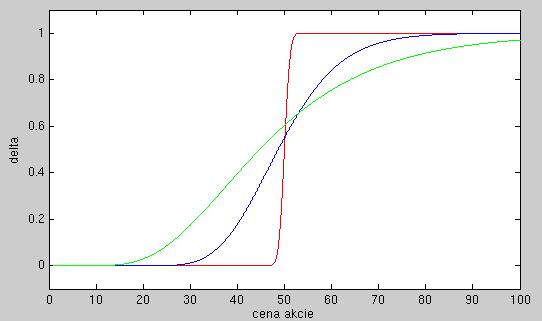
- Na nasledujúcom obrázku sú zobrazené delty troch call opcií v závislosti od ceny akcie. Tieto opcie sa líšia expiráciou:
o 1 deň, o pol roka, o 2 roky. Ostatné parametre sú rovnaké. Priraďte tieto expirácie grafom na obrázku.
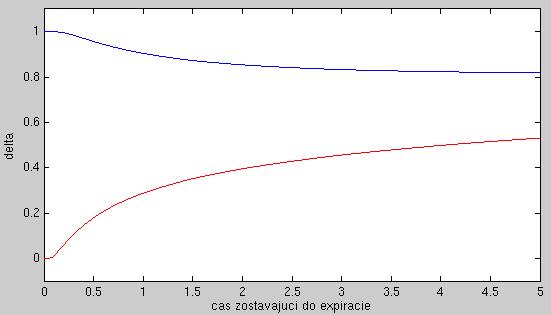
- Na nasledujúcom obrázku sú zobrazené dve delty ako funkcie času zostávajúceho do expirácie. Expiračná cena je v oboch prípadoch 50 USD, líšia sa aktuálnou cenou akcie:
40 USD, 70 USD. Ostatné parametre sú rovnaké. Priraďte tieto expiračné ceny grafom na obrázku.
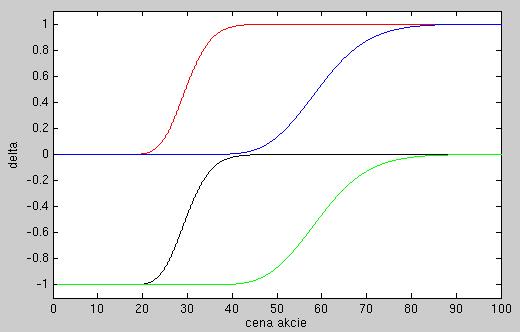
- Na nasledujúcom obrázku sú zobrazené delty štyroch call opcií v závislosti od ceny akcie:
call opcia s E=30, put opcia s E=30, call opcia s E=60, put opcia s E=60. Ostatné parametre sú rovnaké.
Priraďte opcie grafom na obrázku.
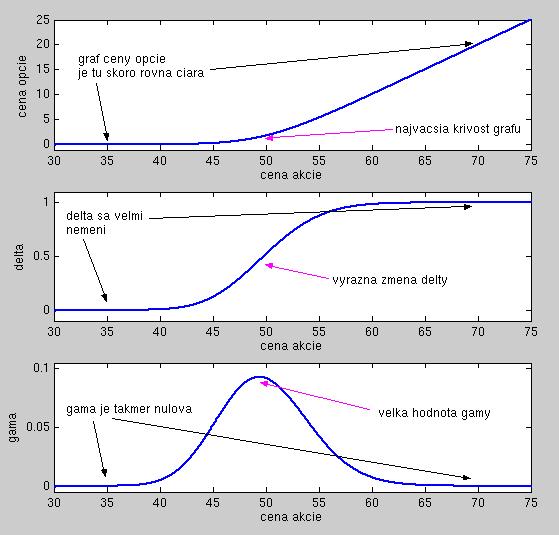
:: Gama ::
- Gama je druhou deriváciou ceny opcie podľa ceny akcie.
- To znamená, že je to derivácia delty podľa ceny akcie. Vyjadruje teda, ako citlivo reaguje delta na zmenu ceny akcie.
- Z call-put parity, že gamy call a put opcie s rovnakými parametrami sa rovnajú. Platí:
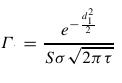
:: Cvičenia (2) ::
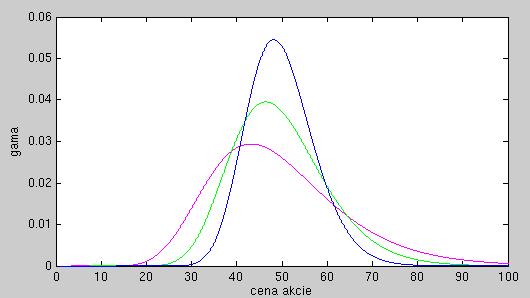
- Na nasledujúcom obrázku sú zobrazené delty troch call opcií v závislosti od ceny akcie. Tieto opcie sa líšia expiráciou:
o rok, o pol roka, o štvrť roka. Ostatné parametre sú rovnaké. Priraďte tieto expirácie grafom na obrázku.
:: Theta ::
- Theta je deriváciou ceny opcie podľa času (t.j. derivácia podľa času zostávajúceho do expirácie s opačným znamienkom).
- Ako závislosť od času môžeme očakávať:
- Z finančnej matematiky vieme, že v prípade cal opcie na akciu nevyplácajúcu dividendy sa cena euŕopskej opcie rovná cene americkej opcie. Je zrejmé, že cena americkej opcie je väčšia, ak do expirácie zostáva viac času. Vzhľadom na rovnosť cien platí to isté aj pre európsky call. Zvýšenie hodnoty času t zodpovedá zmenšeniu času zostávajúceho do expirácie danej opcie. Preto očakávame zápornú thetu.
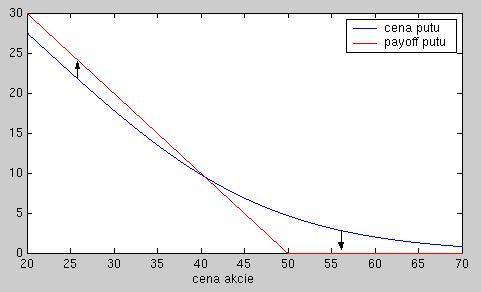
- V prípade put opcie nie je situácia jednoznačná.
- Ak je cena akcie nízka, hodnota putu leží pod payoffom. V čase expirácie bude cena opcie rovná payoffu, takže niekedy do expirácie musí táto cena vzrásť.
- Ak je cena akcie vysoká, hodnota putu leží nad payoffom. V čase expirácie bude cena opcie rovná payoffu, takže niekedy do expirácie musí táto cena klesnúť.
:: Cvičenia (3) ::
- Theta pre call opcie.
-
Nakreslite do jedného grafu ceny niekoľkých call opcií, ktoré sa líšia iba časom zostávajúcim do expirácie, pričom na x-ovej bude cena akcie. Pre aké ceny akcie sa sú ceny opcie najviac citlivé na čas expirácie?
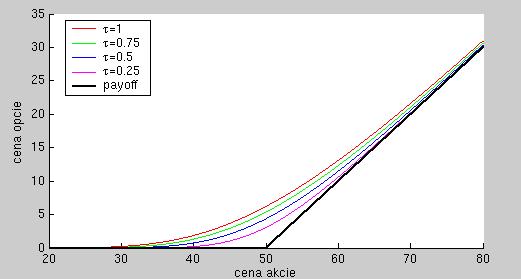
-
Zobrazte závislosť thety call opcie od ceny akcie. Kedy má najväčšiu absolútnu hodnotu -
iba približne, v okolí akej ceny akcie?
-
Theta pre dve rôzne opcie, ktoré sa líšia iba v jednom parametre - v akom?
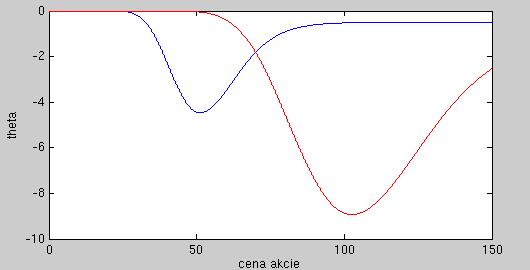
-
Nakreslite do jedného grafu ceny niekoľkých call opcií, ktoré sa líšia iba časom zostávajúcim do expirácie, pričom na x-ovej bude cena akcie. Pre aké ceny akcie sa sú ceny opcie najviac citlivé na čas expirácie?
- Zobrazte závislosť thety put opcie od ceny akcie. Zvoľte pritom také parametre, pri ktorých vidieť, že znamienko thety sa v prípade put opcie môže meniť.
:: Ďalšie príklady na precvičenie ::
- Vypočítajte inflexný bod delty call opcie ako funkcie ceny akcie:
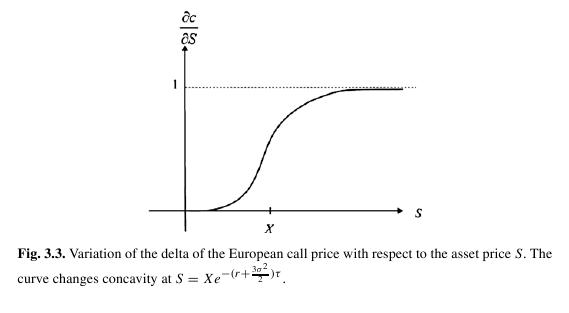
- Vypočítajte elasticitu ceny call opcie podľa ceny akcie:
Dokážte, že je väčšia ako 1 a vypočítajte jej limitu pre cenu akcie idúcu do nekonečna.
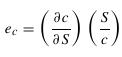
Cvičenia z finančných derivátov, 2011
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/
