Oceňovanie amerických opcií
:: Numerické riešenie ::
- Potrebujeme zaručiť, že cena derivátu neklesne pod payoff - to by bola arbitráž.
- Vieme:
- Cena európskeho callu na akciu bez dividend leží nad payoffom.
- Cena európskeho callu na akciu bez dividend vždy pretne payoff.
- Cena európskeho putu (bez ohľadu na to, či akcia vypláca dividendy alebo nie) vždy pretne payoff
- Takže: Pre amerického callu na akciu bez dividend a ľubovoľného putu je iná ako cena príslušného európskeho derivátu.
- Cena derivátu sa hladko napojí na payoff. - tvrdenie z prednášky, ktorého dôkaz si máte naštudovať v učebnici
- Postup riešenia pre call opciu - opakovanie zo slajdov z prednášky:
- Formulácia v tvare úlohy s voľnou hranicou:
- Transformácia na úlohu o lineárnej komplementarite (už na fixnej oblasti - pre všetky kladné ceny akcie):
- Rovnaká postupnosť tranformácií ako v prípade európskej opcie (tam sme dostali rovnicu vedenia tepla):
- Diskretizácia:
- Numerická schéma na riešenie diskrétnej úlohy:
:: Porovnanie numerického oceňovania európskej a americkej opcie ::
Európska opcia - postup riešenia rovnice pre u
- Vypočítame okrajové podmienky a dosadíme ich do matice riešenia.
- Vypočítame začiatočnú podmienku a dosadíme ju do matice riešenia.
- Výpočet ďalšej časovej vrstvy - SOR metóda
- Začiatočná aproximácia: môžeme zobrať hodnoty z predchádzajúcej časovej vrstvy
- Kontrola podmienky na ukončenie iterácií - norma rezídua
- Výpočet novej iterácie podľa SOR metódy - opakujeme, kým nie je
splnená podmienka na ukončenie iterácií, potom prejdeme na ďalšiu
časovú vrstvu.
Americká opcia - postup riešenia rovnice pre u
- Vypočítame okrajové podmienky. Riešenie musí byť nad transformovaným payoffom => vypočítame max(okrajová podmienka, transformovaný payoff) a dosadíme do matice riešenia
- Vypočítame začiatočnú podmienku a dosadíme ju do matice riešenia.
- Výpočet ďalšej časovej vrstvy - PSOR metóda (projektovaná SOR metóda)
- Začiatočná aproximácia - chceme takú, ktorá bude blízko riešenia, aby sme nemusei robiť veľa iterácií: hodnoty z predchádzajúcej
časovej vrstvy porovnáme s transformovaným payoffom =>
zoberieme max(predchádzajúca časová vrstva, transformovaný payoff)
- Kontrola podmienky na ukončenie iterácií - norma rezídua sa nedá použiť, lebo neriešime sústavu rovníc, použijeme vzdialenosť dvoch nasledujúcich iterácií
- Výpočet novej iterácie podľa PSOR metódy - vypočítame i-tu zložku vektora pomocou SOR metódy a porovnáme s transformovaným payoffom => zoberieme max(SOR iterácia, transformovaný payoff)
a počítame ďalšiu zložku - opakujeme, kým nie je splnená podmienka na
ukončenie iterácií, potom prejdeme na ďalšiu časovú vrstvu.
:: Cvičenie ::
Podľa uvedeného algoritmu naprogramujte numerické oceňovanie amerických call opcií.
:: Ďalšie príklady na precvičenie ::
- Ako sa algoritmus zmení, ak budeme oceňovať put opciu?
- Príklad, ktorý bude na tretej písomke, môžete si teda pripraviť odpoveď:
Cena akcie S sa riadi geometrickým Brownovym pohybom s parametrami 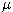 =0.20,
=0.20, 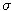 =0.40.
Akcia nevypláca dividendy. Úroková miera je 10 percent. Vypočítajte
cenu put opcie s expiráciou o pol roka a expiračnou cenou 10 USD pre
nasledovné možnosti dnešnej ceny akcie: 0, 2, 4, 6, 8, 10, 12, 14, 16
USD. Uveďte ich s presnosťou na 4 desatiné miesta.
=0.40.
Akcia nevypláca dividendy. Úroková miera je 10 percent. Vypočítajte
cenu put opcie s expiráciou o pol roka a expiračnou cenou 10 USD pre
nasledovné možnosti dnešnej ceny akcie: 0, 2, 4, 6, 8, 10, 12, 14, 16
USD. Uveďte ich s presnosťou na 4 desatiné miesta.
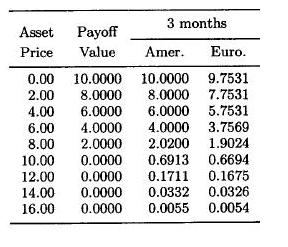
Tu sú výsledky pre opciu s expiráciou o tri mesiace (ostatné parametre
sú rovnaké), môžu byť užitočné pri nastavovaní parametrov numerickej
schémy a spôsobu určovania cien opcií, pri ktorých cena akcie nie je
mrežovým bodom.







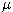 =0.20,
=0.20, 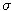 =0.40.
Akcia nevypláca dividendy. Úroková miera je 10 percent. Vypočítajte
cenu put opcie s expiráciou o pol roka a expiračnou cenou 10 USD pre
nasledovné možnosti dnešnej ceny akcie: 0, 2, 4, 6, 8, 10, 12, 14, 16
USD. Uveďte ich s presnosťou na 4 desatiné miesta.
=0.40.
Akcia nevypláca dividendy. Úroková miera je 10 percent. Vypočítajte
cenu put opcie s expiráciou o pol roka a expiračnou cenou 10 USD pre
nasledovné možnosti dnešnej ceny akcie: 0, 2, 4, 6, 8, 10, 12, 14, 16
USD. Uveďte ich s presnosťou na 4 desatiné miesta.