:: Itóov integrál ::

• Pripomeňme si z finančnej matematiky definíciu Itóovho integrálu (pre nenáhodnú funkciu):
  
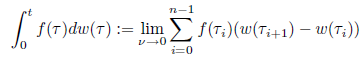
• Vidíme, že hodnota integrálu závisí od Wienerovho procesu, je to teda náhodná premenná. Na začiatku semestra sme generovali Wienerov proces (a iné príbuzné procesy):
  

  function [r]=randn()
      r=rand(1,"normal");
  endfunction
  
  function [w]=wiener(dt,n)
      w(1)=0; 
      for i=1:n
          dw=sqrt(dt)*randn();
          w(i+1)=w(i)+dw;
      end;
      w=w';
  endfunction
  

• Zvoľme si funkciu, ktorej integrál budeme počítať, napríklad na intervale [0,1] budeme integrovať funkciu:
  

  function [f]=f(x)
      f=x^2;
  endfunction
  

• Vygenerujme trajektóriu Wienerovho procesu na nejakom delení tohto intervalu:
  

  dt=0.01;
  n=100;
  t=(0:dt:n*dt);
  
  w=wiener(dt,n);
  

• Cvičenie 1 - simulácie:
  • Pomocou sumy, ktorej limitou je definovaný Itóov integrál, vypočítajte aproximáciu hodnoty integrálu pre túto trajektóriu Wienerovho procesu.
  • Vygenerujte viac trajektórií Wienerovho procesu, zaznamenávajte hodnotu aproximácie Itóovho integrálu, priebežnú (na základe doterajších simulácií) strednú hodnotu a disperziu.
  • Ako vyzerá histogram získaných hodnôt? Na čom sa stabilizujú pribežné hodnoty strednej hodnoty a disperzie?
• Cvičenie 2 - výpočet:
  • Vypočítajte pravdepodobnostné rozdelenie sumy, ktorej limitou je definovaný Itóov integrál.
  • Spravte limitu a určte pravdepodobnostné rozdelenie Itóovho integrálu
  • Porovnajte s výsledkami z konkrétneho príkladu a simulácií v predchádzajúcej úlohe.

:: Jednofaktorový short rate model ::

• Úrokové miery - napríklad Euribor:
  
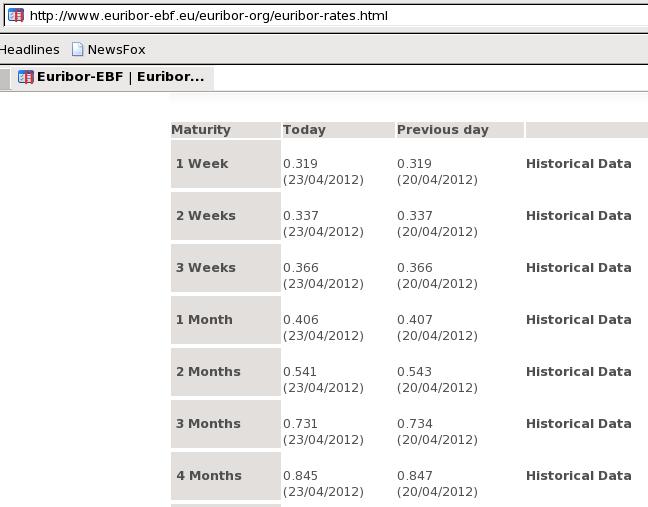
• Short rate - okamžitá úroková miera, aproximuje sa úrokovou mierou s krátkou splatnosťou
• Okamžitá úroková miera sa modeluje stochastickou diferenciálnou rovnicou:
  
  teda trend vo vývoji úrokovej miery + náhodné fluktuácie okolo trendu
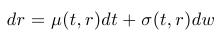
• Jednofaktorový model - jedna stochastická diferenciálna rovnica pre r, t. j. jeden zdroj náhodnosti vo vývoji okamžitej úrokovej miery (jeden Wienerov proces).

:: Vašíčkov model :::

• Stochastická diferenciálna rovnica pre okamžitú úrokovú mieru:
  
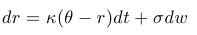
• Vlastnosť mean-reversion (priťahovanie k dlhodobej hodnote, k limitnej hodnote) - pre strednú hodnotu platí:
  
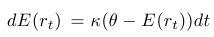
• Volatilita je konštantná, nezávisí teda od aktuálnej hodnoty úrokovej miery
• S procesom, ktorý sa vo Vašíčkovom modeli používa na modelovanie okamžitej úrokovej miery, sme sa už zaoberali na treťom cvičení. Zopakujme si závislosť priebehu procesu od parametrov podľa cvičenia(1)/1.

:: Pravdepodobnostné rozdelenie úrokových mier ::

• Odvodíme riešenie uvedenej stochastickej diferenciálnej rovnice v integrálnom tvare:
  
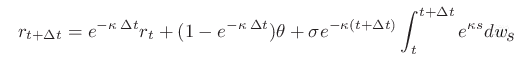
• Na základe tohto vyjadrenia odvoďte podmienené rozdelenie úrokovej miery, ak poznáme jej hodnotu r₀ v čase 0 - je to normálne rozdelenie 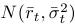s parametrami
  
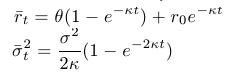
• Znalosť tohoto rozdelenia nám umožňuje:
  • Vygenerovať realizáciu procesu pre zadané parametre a začiatočnú hodnotu úrokovej miery.
  • Odhadovať parametre procesu z dát.
• Upozornenie: V literatúre sa požívajú rôzne označenia pre lineárnu funkciu driftu, treba si vždy pozrieť, s akým driftom sa pracuje.

::Cvičenia (1) ::

1. Na začiatku semestra, keď sme spomínali Vašíčkov model, sme pracovali s parametrami z článku Athanasios Episcopos: Further evidence on alternative continuous time models of the short-term interest rate. Journal of International Financial Markets, Institutions and Money 10 (2000) 199-212, kde autor odhadoval modely úrokových mier. Všeobecný model, ktorým sa zaoberal, je
   
   Znovu zoberieme parametre pre Nový Zéland:
   
   
   
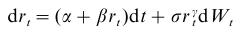
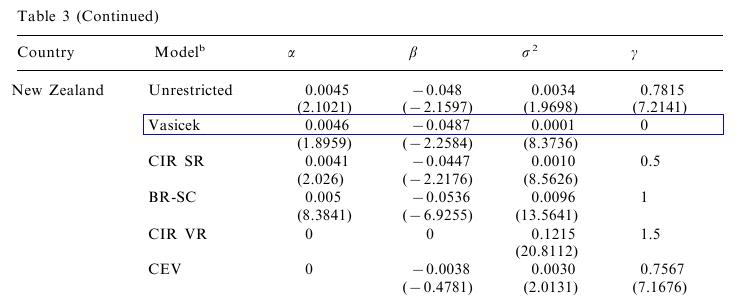
   • Preveďte tieto parametre tak, aby sme proces mali vyjadrený ho pomocou parametrov 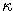, , 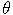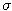. Zvoľte si začiatočnú hodnotu úrokovej miery a vygenerujte trajektóriu jej ďalšieho vývoja.
     
     
   • Na začiatku semestra sme tento proces simulovali Euler-Marujamouvou aproximáciou. Porovnajte rozdelenie úrokovej miery získané touto aproximáciou s presným rozdelením, ak je časový krok 1 deň, 1 týždeň, 1 mesiac, 1 rok. Ďalej budeme požívať presné rozdelenie.
     
     
   • Predpokladajte, že dnešná hodnota úrokovej miery je 4.5 percenta. Aká je stredná hodnota úrokovej miery o týždeň, o mesiac a o rok? Zostrojte pre tieto úrokové miery intervalové odhady (stredná hodnota +/- 2*štandardná odchýlka).
     
     
   • Aké je limitné rozdelenie úrokovej miery. Nakreslite graf hustoty tohto limitného rozdelenia. Doplňte do grafu hustoty rozdelenia úrokovej miery o mesiac, o rok, ... - tak, aby ste videli konvergenciu týchto hustôt k limitnej hustote.
     
     
   • Jednou z nevýhod Vašíčkovho modelu je možnosť záporných úrokových mier. Vypočítajte pravdepodobnosť zápornej úrokovej miery v nasledovných prípadoch:
     • limitné rozdelenie úrokovej miery
     • úroková miera o mesiac, ak jej dnešná hodnota je 5 percent.
     • úroková miera o mesiac, ak jej dnešná hodnota je pol percenta.
     • úroková miera o týždeň, ak jej dnešná hodnota je 5 percent.
     • úroková miera o týždeň, ak jej dnešná hodnota je pol percenta.
     
     
   • Nájdite príklad takých parametrov, aby predchádzajúce pravdepodobnosti záporných úrokových mier boli väčšie (pri takýchto pravdepodobnostiach zrejme nie je model vhodný).

:: Metóda maximálnej vierohodnosti na odhadovanie parametrov ::

• Podmienené rozdelenie úrokových mier je normálne, preto funkcia vierohodnostije súčin hustôt normálnych rozdelení. Odhady parametrov sa dajú explicitne vyjadriť.
  
  
• Damiano Brigo, Fabio Mercurio: Interest Rate Models - Theory and Practice. Second Edition. Springer, 2007. Kapitola 3.1.2, str. 61-62:
  
  [books.google.com]
  
  
• Môže sa vám hodiť nasledujúci skript, v ktorom sú prepísané tieto vzorce pre odhady: [vasicekMLE.sce]

:: Cvičenia (2) ::

1. Ako z týchto odhadov dostaneme odhady parametrov 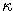, , 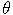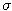? Odvoďte príslušnú transformáciu.

:: Ďalšie príklady na precvičenie ::

• Stiahnite si dáta úrokovej miery (napr. 3M treasury bills, Euribor s krátkou dobou splatnosti a pod.) zo zvoleného časového intervalu. Zobrazte ich vývoj. Zdroje dát - napríklad:
  • Federal Reserve Statistical Release
  • Euribor.org
  • Bank of Canada
• Odhadnite parametre Vašíčkovho modelu a transformujte ich na parametre , , .
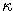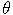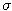• Pre zvolenú začiatočnú hodnotu úrokovej miery nakreslite do jedného grafu strednú hodnotu jej ďalšieho vývoja, intervaly spoľahlivosti a niekoľko simulácií.
• Nájdite limitné rozdelenie úrokovej miery.

---

---