:: Európska call a put opcia ::

• Európske opcie:
  • Európska call opcia je kontrakt, v ktorom majiteľ, opcie získava právo (ale nie povinnosť) kúpiť akciu v presne určenom expiračnom čase za vopred dohodnutú expiračnú cenu E.
  • Európska put opcia je kontrakt, v ktorom majiteľ, opcie získava právo (ale nie povinnosť) predať akciu v presne určenom expiračnom čase za vopred dohodnutú expiračnú cenu E.
• Payoff = hodnota v čase expirácie
  • Call opcia má payoff: max(S-E,0)
  • Put opcia má payoff: max(S-E,0)
• Profit = payoff znížený o odúročenú cenu opcie

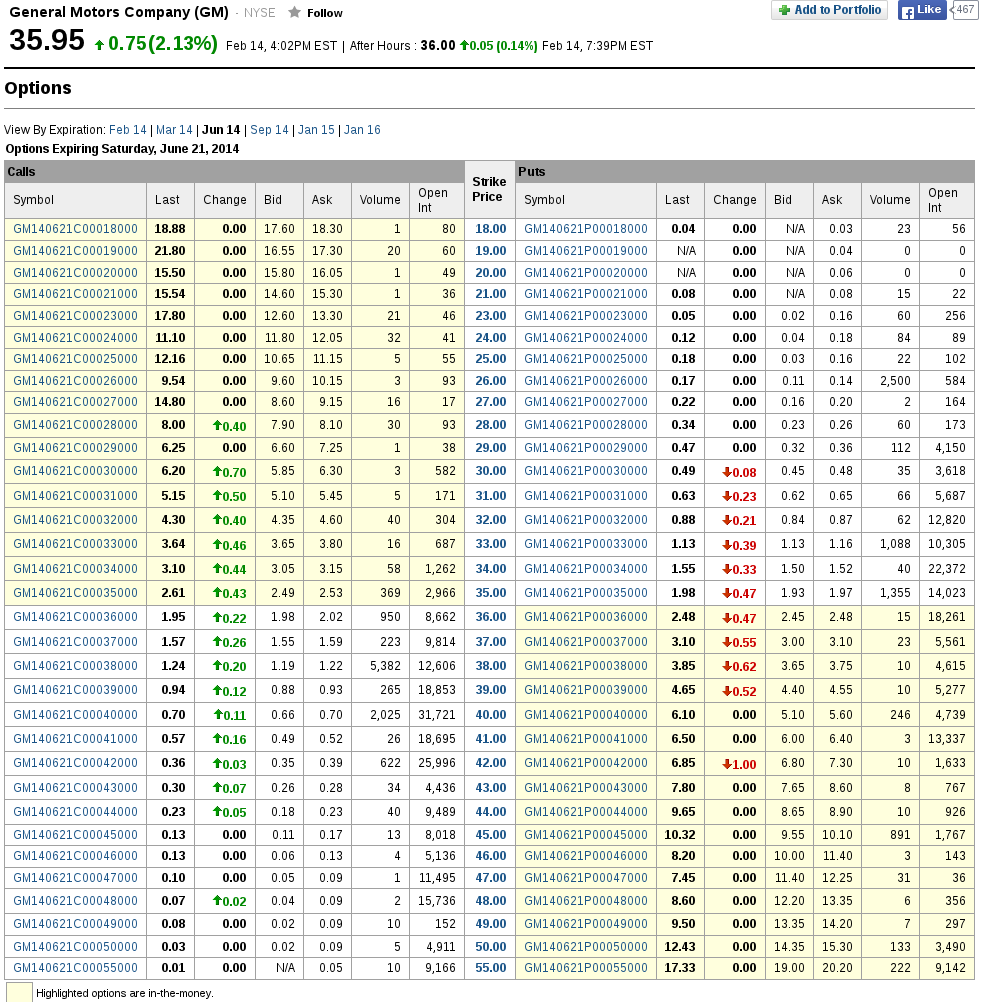
:: Z prednášky: príklady s reálnymi cenami opcií ::

Keďže na prednáške nešiel dataprojektor, prejdeme si teraz slajdy využívajúce reálne ceny akcií a opcií:

• vnútorná a časová hodnota opcie
• bid a ask ceny

:: Symboly opcií ::

Ako je možné, že máme viac opcií s rovnakou expiračnou cenou a rovnaký časom do expirácie?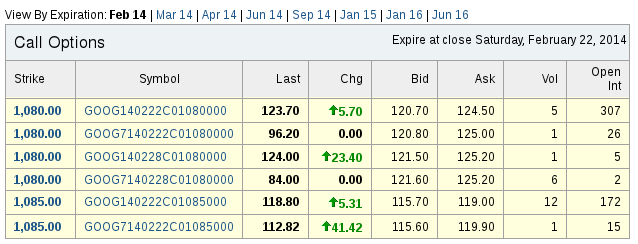

• Opcie väčšinou expirujú tretiu sobotu v mesiaci (a obchodovanie s nimi sa končí predchádzajúci piatok), ale:
  • nie všetky
  • pre nietoré akcie existujú aj tzv. mini options: štandardne sa opcie nakupujú v stovkách, mini opcie v desiatkach kusov

• Všetko sa dá vyčítať zo symbolu opcie:
  • na začiatku: symbol akcie
  • ak ide o mini opciu, za symbolom akcie nasleduje číslo 7
  • čas expirácie vo formáte YYMMDD
  • typ opcie: call/put, zapísané ako C/P
  • expiračná cena: posledné tri desatinné miesta sú centy

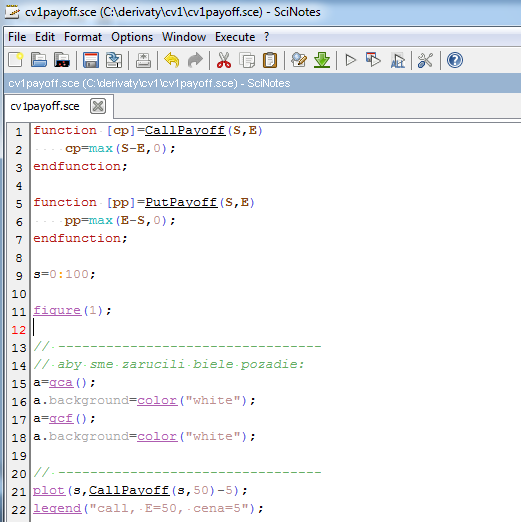
:: Payoff a profit diagramy v Scilabe ::

• Definujeme v Scilabe funkcie, ktoré vrátia payoff call opcie

  function [cp]=CallPayoff(S,E)
     cp=max(S-E,0);
  
  endfunction; 
  

  a put opcie

  function [pp]=PutPayoff(S,E)
     pp=max(E-S,0);
  endfunction; 
  

• Rozdiely oproti Matlabu:
  • na konci definície funkcie treba endfunction,
  • funkcie môžu byť definované na ľubovoľnom mieste skriptu, tieto definujeme na začiatku.

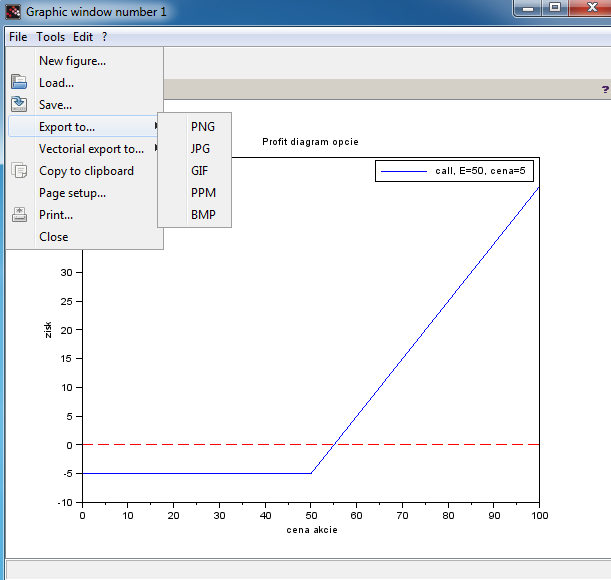
• Teraz môžeme kresliť payoff diagram a profit diagram (payoff znížený o cenu stratégie - týmto vlastne predpokladáme, že úroková miera je nulová, ale vzhľadom na nízke úrokové miery a nie veľmi dlhý čas zostávajúci do expirácie to nespôsobuje veľký rozdiel).

[cv1payoff.sce] - súbor pre Scilab: definícia funkcií na výpočet payoffu call a put opcie doluuvedený kód na vykreslenie obrázku

Stiahnite si ho a spustite.

Výsledok: Môžeme si vybrať formát a obrázok uložiť - buď pomocou Export to (napr. do png) alebo Vectorial export to (napr. do eps).

:: Cvičenia (1) ::

1. Predpokladajme, že vlastníme jednu put opciu s expiračnou cenou 60 USD, ktorá stojí 7 USD a jednu call opciu s tou istou expiračnou cenou, ktorá stojí 5 USD.
   • Nakreslite payoff a profit diagram. Aké očakávanie o vývoji ceny akcie vyjadruje táto stratégia?
   • Pre aké ceny akcie v čase expirácie dosiahneme zisk?
   • Aký maximálny zisk môžeme dosiahnuť? Akú maximálnu stratu? Kedy sa dosahuje tento maximálny zisk, resp. maximálna strata?

:: Moneyness ::

Týmto pojmom sa rozlišujú opcie v závislosti od vzťahu expiračnej ceny opcie a aktuálnej ceny opcie.

• ATM (at the money): cena akcie sa rovná expiračnej cene
• ITM (in the money): ak by opcia expirovala teraz, bolo by výhodné uplatniť ju
• OTM (out of the money): ak by opcia expirovala teraz, nebolo by výhodné uplatniť ju

:: Kombinované stratégie ::

Link: http://www.theoptionsguide.com/

• Neutral (non-directional) strategies - používajú sa v prípade, že investor nevie, ktorým smerom sa cena akcie pohne. Líšia sa tým, či predpokladáme malú alebo veľkú zmenu ceny akcie (bez špecifikácie smeru tejto zmeny).
  • Ak očakávame malú zmenu ceny, možné stratégie sú napríklad:
    • Short straddle: http://www.theoptionsguide.com/short-straddle.aspx
    • Short strangle: http://www.theoptionsguide.com/short-strangle.aspx
    • Long call condor: http://www.theoptionsguide.com/condor.aspx
    • Long call butterfly: http://www.theoptionsguide.com/butterfly-spread.aspx
  • Ak očakávame veľkú zmenu ceny, možné stratégie sú napríklad:
    • Long straddle: http://www.theoptionsguide.com/long-straddle.aspx
    • Long strangle: http://www.theoptionsguide.com/long-strangle.aspx
    • Short call condor: http://www.theoptionsguide.com/short-condor.aspx
    • Short call butterfly: http://www.theoptionsguide.com/short-butterfly.aspx
• Bearish strategies (medvedie stratégie) - založené sú na predpoklade investora, že cena akcie klesne. Príkladmi takýchto stratégií sú:
  • Bear call spread: http://www.theoptionsguide.com/bear-call-spread.aspx
  • Bear put spread: http://www.theoptionsguide.com/bear-put-spread.aspx
• Bullish strategies (býčie stratégie) - založené sú na predpoklade investora, že cena akcie vzrastie. Príkladmi takýchto stratégií sú:
  • Bull call spread: http://www.theoptionsguide.com/bull-call-spread.aspx
  • Bull put spread: http://www.theoptionsguide.com/bull-put-spread.aspx

:: Reálne ceny opcií ::

• http://finance.yahoo.com, http://finance.google.com
• Zadáme kód alebo ho vyhlľadáme firmu podľa názvu.
• Pre zvolemú firmu zobrazíme opcie. Ukážka:
  
• Opciu môžeme kúpiť za ask, predať za bid.

:: Cvičenia (2) ::

1. Vyberte si jednu stratégiiu z prehľadu a pomocou reálnych cien uvedených hore zostrojte jej payoff a profit diagram. Aké presvedčenie o budúcom vývoji akcie vyjadruje takáto stratégia? Pre aké ceny akcie v čase expirácie bude zisková?

:: Obmedzenia na ceny opcií ::

• Označme c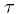(S,,E), p(S,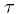,E) cenu call, resp. put opcie s expiračnou cenou E, ak aktuálna cena akcie je S a do expirácie opcie zostáva čas .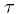
• Ceny opcií musia vyhovovať určitým nerovnostiam, ktoré vyplývajú z neprípustnosti arbitráže. Myšlienka ich dôkazu je nasledovná:
  • Uvažujme dve portfóliá (zložené z akcií, opcií a dlhopisov).
  • Nech v čase expirácie opcií platí pre hodnoty týchto portfólií nerovnosť P₁ 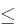P₂
  • Potom rovnaká nerovnosť pre hodnoty portfólií musí platiť aj vo všetkých predchádzajúcich časoch.

• Príklad I. z prednášky: nerastúcosť pre call opciu
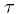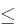  Dokázali sme, že c(S,,E₁) c(S,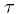,E₂) pre E₂ 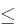E₁
  
  Cvičenie: Uvažujme nasledovné ceny call opcií:

  Expiračná cena	Cena call opcie
  10	30
  15	26
  20	27
  25	23
  30	19

  Nájdite arbitrážnu príležitosť - teda takú stratégiu, ktorá bez ohľadu na cenu akcie v čase expirácie opcií prinesie zisk. Nakreslite profit diagram vašej stratégie.
  
  Riešenie: Podľa prechádzajúceho príkladu by malo platiť c(15)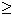 c(20). Pre naše dáta to však neplatí, máme c(15) < c(20). Čo teda spravíme:
  • kúpime to, čo je lacnejšie, ako by malo byť - na našom prípade c(15)
  • predáme to, čo je drahšie, ako by malo byť - na našom prípade c(20)

  [cv1arbitraz.sce] - súbor pre Scilab: dáta - ceny opcií vykreslenie závislosti ceny opcie od jej expiračnej ceny Stiahnite si ho a dopíšte vykreslenie profit diagramu arbitrážnej príležitosti.

• Príklad I. z prednášky: nerastúcosť pre call opciu
  Dokázali sme, že c(S,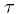,E) je konvexnou funkciou expiračnej ceny.
  
  Cvičenie: Uveďte príklad cien opcií, pre ktoré táto závislosť nie je konvexná a nájdite arbitráž.

:: Ďalšie príklady na precvičenie ::

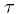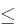1. Dokážte, že p(S,,E₁) p(S,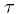,E₂) pre E₁ 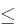E₂ . Zostavte príklad arbitrážnej príležitosti, ak táto nerovnosť neplatí (s konkrétnymi číslami).
   
   
2. Dokážte, že funkcia p(S,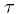,E) je konvexnou funkciou expiračnej ceny E. Zostavte príklad arbitrážnej príležitosti, ak táto nerovnosť neplatí (s konkrétnymi číslami).
   
   
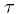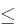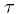3. Dokážte, že S - E exp(-r ) c(S,,E) 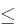S, kde r je úroková miera. Zostavte príklad arbitrážnej príležitosti, ak táto nerovnosť neplatí (s konkrétnymi číslami).
   
   
4. Predpokladajme, že úroková miera je nulová. Súčasná cena akcie je 10 USD, a na trhu sú dostupné opcie s expiračnou cenou 12 USD, ktoré expirujú o mesiac. Call opcia stojí 3 USD, put opcia stojí 4 USD. Nájdite arbitráž.
   
   
5. Uvažujme call a put opciu, ktoré majú rovnakú expiračnú cenu, 55 USD a obidve expirujú o rok. Cena akcie je 53 USD a cena callu je o 0.1 USD vyššia ako cena putu. Čomu sa rovná úroková miera?
   
   
6. [Vzorová písomka, 2008]
   
   
   
   
7. Nájdite kombinácie call a put opcií, ktoré majú nasledovné payoffy:
   
   
   
   
   
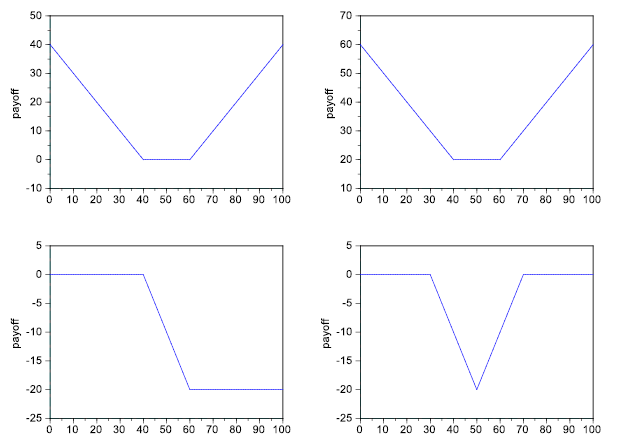
8. [Písomka, 2009]
   
   
   
   
   
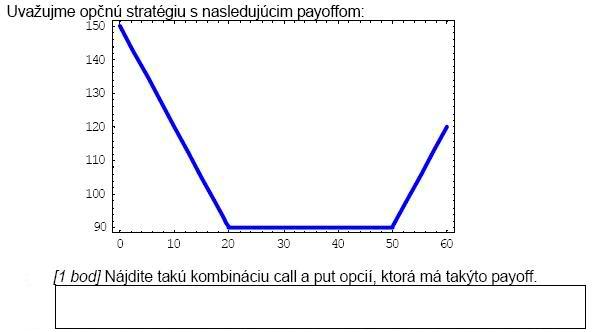
9. [Písomka, 2009]
   
   
   
   

---