:: Ceny dlhopisov v jednofaktorovom short rate modeli ::

• Opakovanie - okamžitá úroková miera sa modeluje stochastickou diferenciálnou rovnicou.
  
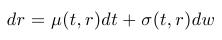
• Odvodí sa PDR pre cenu dlhopisu P
  
  ktorá závisí od okamžitej úrokovej miery tau a od času t. Funkcia lambda sa nazýva trhová cena rizika.
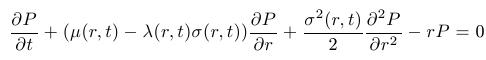
• V čase expirácie je hodnota dlhopisu rovná jednej, teda P(T,r)=1 pre každé r.
• Cenami dlhopisov sú určené úrokové miery:
  

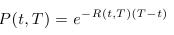
Ceny dlhopisov vo Vašíčkovom modeli

• Uvažujeme konštantnú trhovú cenu rizika, teda funkcia lambda(t,r) sa identicky rovná konštante lambda.
• Zavedieme substitúciu - namiesto času budeme uvažovať čas tau zostávajúci do maturity, t.j.
  
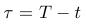
• Riešenie PDR pre cenu dlhopisu sa potom dá nájsť v tvare
  
  kde funkcie A, B sú:
  

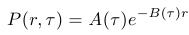
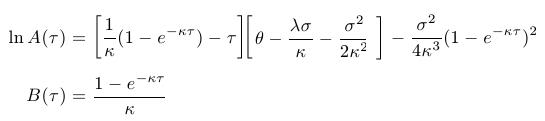
:: Cvičenia ::

1. Zvoľte si parametre Vašíčkovho modelu článku z minulého cvičenia. Zvoľte si hodnotu okamžitej úrokovej miery a zakreslite výnosové krivky pre niekoľko rôznych trhových cien rizika.
   
   
2. Zvoľte si parametre Vašíčkovho modelu článku z minulého cvičenia. Zvoľte si hodnotu trhovej ceny rizika. Pre niekoľko hodnôt okamžitej úrokovej miery zakreslite do jedného grafu výnosové krivky. Dokážte, že ak tau ide do nekonečna, tak úrokové miery so splatnosťou tau konvergujú k hodnote
   
   
   
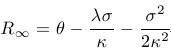
3. Zvoľte si parametre Vašíčkovho modelu článku z minulého cvičenia. Predpokladjme, že limita výnosových kriviek sa rovná trom štvrtinám limitnej hodnoty okamžitej úrokovej miery. Vypočítajte trhovú cenu rizika.
   
   
4. Uvažujme parametre z predchádzajúcej otázky. Nájdite príklad takej hodnoty okamžitej úrokovej miery, pre ktorú nie je príslušná výnosový krivka monotónna.
   
   
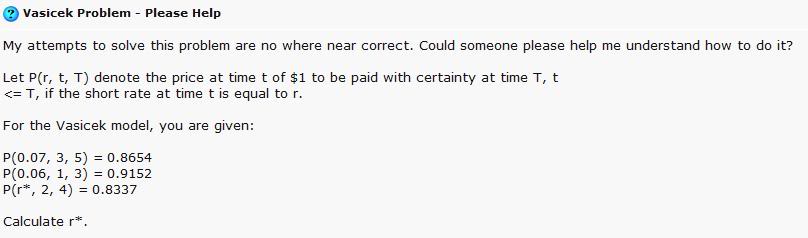
5. Otázka o Vašíčkovom modeli z internetového diskusného fóra:
   

---