Stochastické diferenciálne rovnice
:: Stochastické diferenciálne rovnice ::

| Stiahnite si [cv3sdr.sce] - súbor pre Scilab k tomuto cvičeniu. |
- Nenáhodná funkcia môže byť zadaná ako riešenie obyčajnej diferenciálnej rovnice - máme daný vzťah medzi diferenciálom funkcie a diferenciálom času. Napr. dx(t)=x(t) dt, spolu so začiatočnou podmienkou x(0) určuje (deterministickú, t.j. nenáhodnú) funkciu x(t).
- Analógia pre náhodné funkcie - vzťah medzi diferenciálom funkcie, diferenciálom času a diferenciálom Wienerovho procesu dw. Takto dostávame stochastické diferenciálne rovnice. Ich riešením je náhodná funkcia. Napríklad:
- dx=2dt+3dw, začiatočná podmienka x(0)=0 - toto je Brownov pohyb: x(t)=2t+3w(t)
- dx=2dt+3dw, začiatočná podmienka x(0)=1 - posunutý Brownov pohyb, začína z jednotky: x(t)=1+2t+3w(t)
- dx=10[1-x(t)] dt + 0.25 dw(t), x(0)=0.5 - tiež sa dá zapísať explicitne, ale toto vyjadrenie je komplikovanejšie. Dobrú predstavu o priebehu takéhoto procesu však dostaneme pomocou simulácií jeho trajektórií.
- Pozrime sa teda na proces tvaru
kde
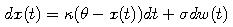
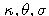 sú kladné konštanty. Takýto proces sa nazýva Ornstein-Uhlenbeckov proces.
sú kladné konštanty. Takýto proces sa nazýva Ornstein-Uhlenbeckov proces.
Najjednoduchším pôsobom, ako získať aproximáciu riešenia stochastickej diferenciálnej rovnice je nahradiť diferenciály diferenciami (analógia Eulerovej metódy pre obyčajné diferenciálne rovnice, pri stochastických diferenciálnych rovniciach sa nazýva Euler-Marujamova metóda):
Ukážka: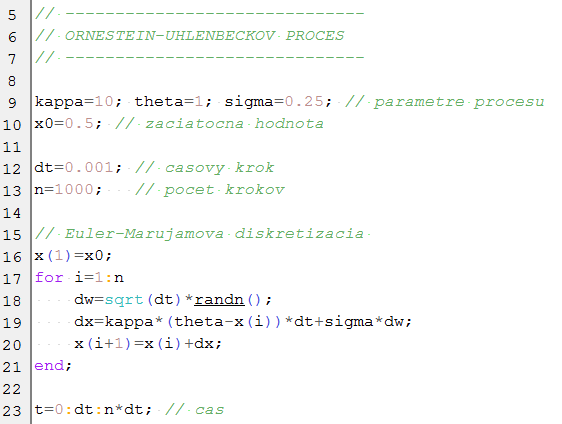
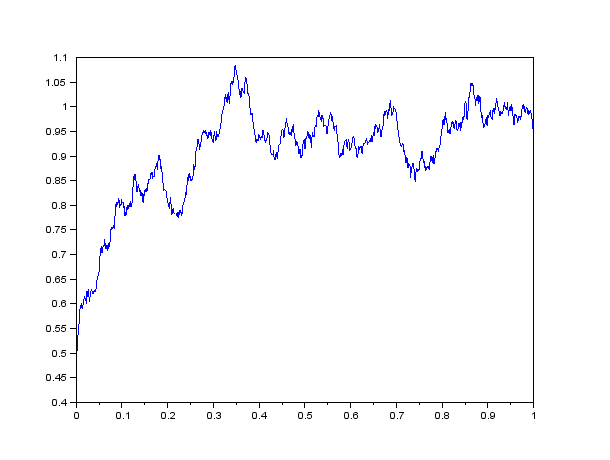
- Terminológia: Deterministická časť procesu (pri časovom diferenciáli dt) sa nazýva drift, stochastická časť (pri diferenciáli Wienerovho procesu dw) sa nazýva volatilita.
:: Cvičenia (1) ::
- Definujte v Scilabe funkciu, ktorá vygeneruje vektor s realizáciou OU procesu so zadanou začitočnou hodnotou a zadanými parametrami procesu a časového delenia.
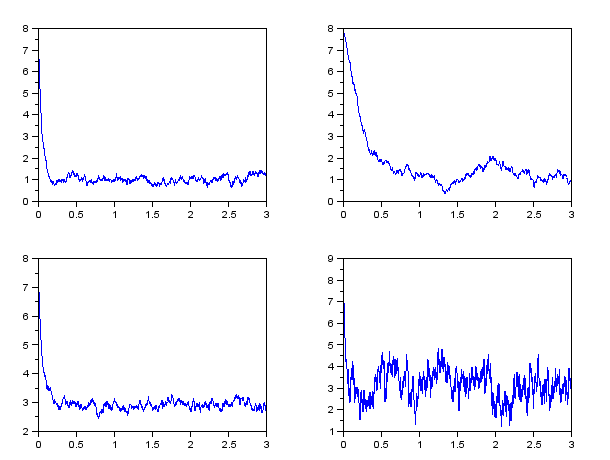
Zakreslite niekoľko realizácií Orstein-Uhlenbeckovho procesu
so zvolenými parametrami..
Všímajte si, ako závisí typický priebeh procesu od parametrov.
Priraďte nasledujúce hodnoty parametrov k ich trajektóriám: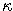 = 20,
= 20, 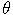 = 1,
= 1, 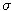 = 1
= 1
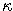 = 3,
= 3, 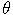 = 1,
= 1, 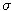 = 1
= 1
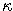 = 20,
= 20, 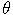 = 3,
= 3, 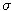 = 5
= 5
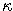 = 20,
= 20, 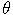 = 3,
= 3, 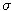 = 1
= 1
- Ornstein-Uhlenbeckov proces sa používa napríklad pri modelovaní úrokových mier. Vašíčkov model
predpokladá, že okamžitá úroková miera (prakticky - pri analýze
reálnych dát - úroková miera na krátky čas) sa riadi
Ornstein-Uhlenbeckovym procesom.
V článku Athanasios Episcopos: Further evidence on alternative continuous time models of the short-term interest rate. Journal of International Financial Markets, Institutions and Money 10 (2000) 199-212 autor odhadoval modely úrokových mier. Všeobecný model, ktorým sa zaoberal, jeŠpeciálnou voľbou niektorých parametrov dostávame konkrétne modely, jedným z nich je aj Vašíčkov model. Výsledky pre Nový Zéland (odhady parametrov pre mesačné dáta od apríla 1986 do apríla 1998 sú v nasledujúcej tabuľke: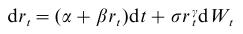 Zdroj: (Episcopos, 2000)
Zdroj: (Episcopos, 2000)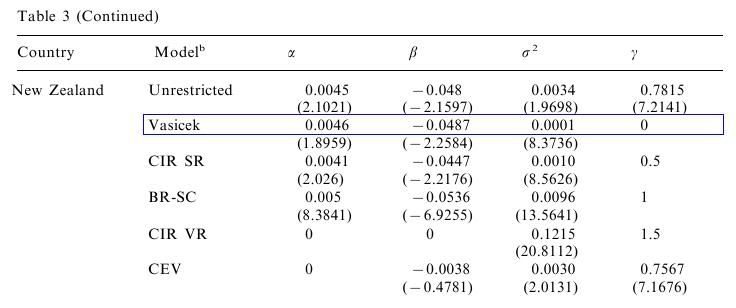
- Proces je v inom tvare, ako sme definovali Ornstein-Uhlenbeckov proces. Vyjadrite ho pomocou parametrov
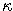 ,
, 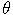 ,
, 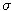 . K akej hodnote sa dlhodobo približuje úroková miera?
. K akej hodnote sa dlhodobo približuje úroková miera?
- Vygenerujte priebeh vývoja úrokovej miery na základe odhadnutých parametrov Vašíčkovho modelu. Zakreslite do jedného grafu niekoľko možných priebehov, štartujúcich z rovnakej začiatočnej hodnoty.
- Proces je v inom tvare, ako sme definovali Ornstein-Uhlenbeckov proces. Vyjadrite ho pomocou parametrov
:: Itóova lema ::

|
Kijoši Itó (1915 - 2008), zakladateľ teórie stochastických diferenciálnych rovníc.
|
- Na predchádzajúcom cvičení sme mali predpis procesu (geometrický Brownov pohyb - cena akcie) x(t) zadaný explicitne v tvare x(t)=....
Na začiatku tohto cvičenia sma pracovali s iným zápisom - pomocou
diferenciálov sme definovali Ornestein-Uhlenbeckov proces. Teraz si
ukážeme ich vzájomný vzťah.
- Pre nenáhodnú funkciu vieme derivovaním napísať obyčajnú diferenciálnu rovnicu, ktorú spĺňa. Napr. pre x(t)=t2 platí dx(t)=2 t dt. Naopak, pre zadanú obyčajnú diferenciálnu rovnicu vieme v niektorých prípadoch napísať explicitné riešenie.
- Ako derivovať náhodnú funkciu? Uvažujme funkciu
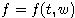 , kde w je
Wienerov proces a počítajme rozvoj:
Tu si treba uvedomiť, že
, kde w je
Wienerov proces a počítajme rozvoj:
Tu si treba uvedomiť, že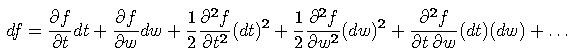
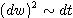 , a teda máme:
To znamená, že
, a teda máme:
To znamená, že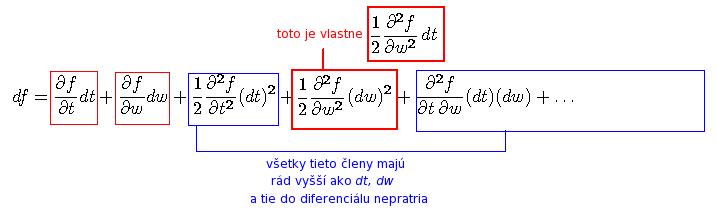
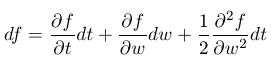
-
Vo všeobecnosti dostávame takýmto postupom Itóovu lemu:
Nech x je proces daný rovnicoua f(t,x) je hladká funkcia. Potom f vyhovuje stochastickej diferenciálnej rovnici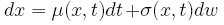
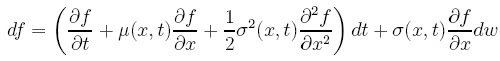
- Ukážky použitia Itóovej lemy pri oceňovaní derivátov:
- Vývoj ceny akcie je daný stochastickou diferenciálnou rovnicou pre S. Cena derivátu V závisí od času t a od ceny akcie S. Itóova lema dáva predpis pre stochastickú diferenciálnu rovnicu, ktorú spĺňa cena derivátu V(t,S). Táto rovnica sa využije pri odvodzovaní ceny derivátu.
- Vývoj okamžitej úrokovej miery r je daný stochastickou diferenciálnou rovnicou (napríklad Ornstein-Uhlenbeckov proces vo Vašičkovom modeli). Cena derivátu V závisí od času t a od okamžitej úrokovej miery r. Ďalej je postup analogický: Itóova lema dáva predpis pre stochastickú diferenciálnu rovnicu, ktorú spĺňa cena derivátu V(t,r). Táto rovnica sa využije pri odvodzovaní ceny derivátu.
:: Cvičenia (2) ::
- Príklad z prednášky: Dopočítajte diferenciál d(B3) z výpočtu z obrázku, kde B je Wienerov proces.

-
Vypočítajte diferenciály nasledovných funkcií:
- x1(t)=ln y(t), kde dy(t)= 2y(t) dt + 3y(t) dw(t),
- x2(t)=-2exp(-10 t + 2 w(t)).
- Uvažujme proces
Na obrázku je niekoľko realizácií tohto procesu.
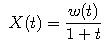 Dokážte, že tento proces vyhovuje stochastickej diferenciálnej rovnici
Dokážte, že tento proces vyhovuje stochastickej diferenciálnej rovnici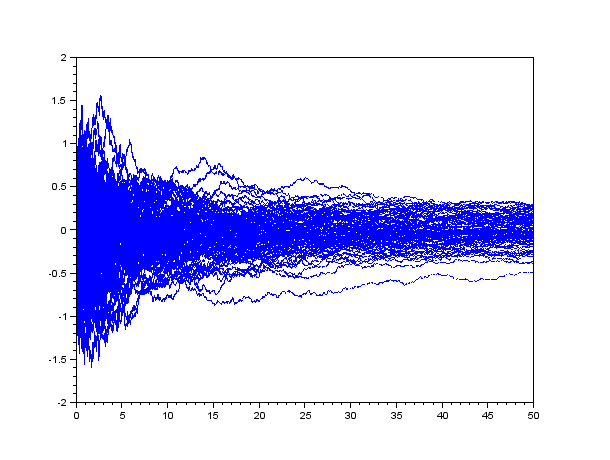
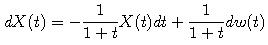
- Porovnanie priebehu procesu a Euler-Marujamovej diskretizácie
Uvažujme proces z predchádzajúceho cvičeniaa stochastickú diferenciálnu rovnicu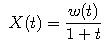 ktorú spĺňa.
ktorú spĺňa.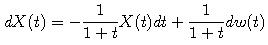
Pomocou toho istého Wienerovho procesu vygenerujte trajektóriu tohto procesu a Euler-Marujamovej diskretizácie stochastickej difrenciálnej rovnice. Doplňte chýbajúce časti kódu podľa uvedenej osnovy:
T=5; // casovy interval [0,T] dt=0.001; // casovy krok // vektor casov t=... // SPOLOCNY Wienerov proces w w=... // x = proces x=... // xD = diskretizacia SDR xD(1)=.. for ... xD(i+1)=... end; plot(t,x); plot(t,xD,'r');
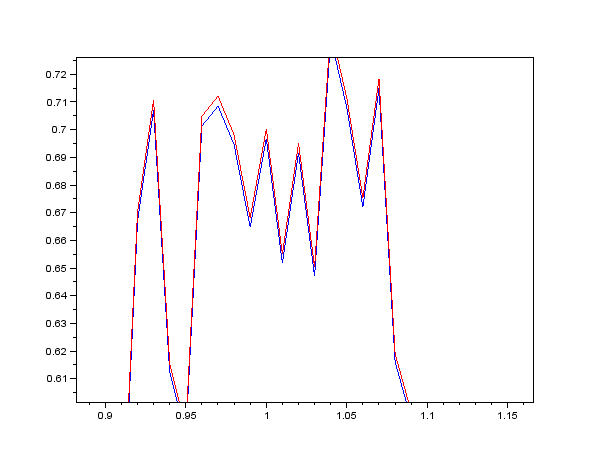
Ukážka pre časový krok dt=0.05:Ukážka pre časový krok dt=0.01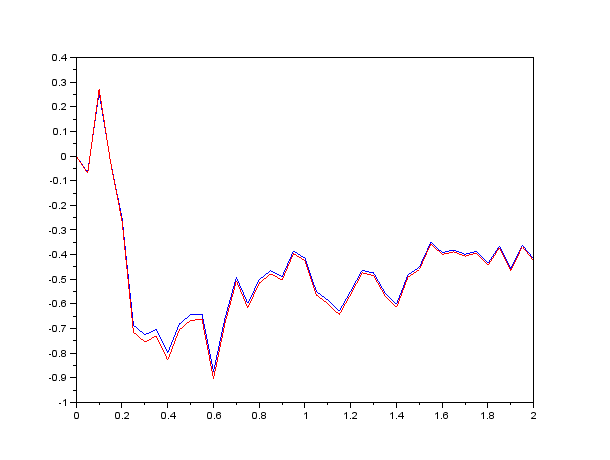 Zoom z predchádzajúceho grafu:
Zoom z predchádzajúceho grafu: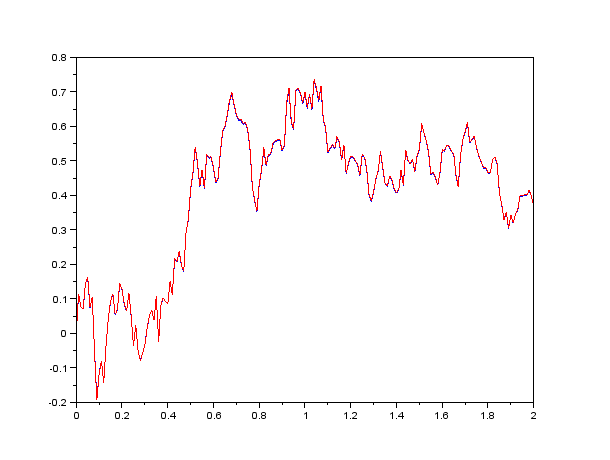
:: Ďalšie príklady na precvičenie ::
- Uvažujme stochastickú diferenciálnu rovnicu
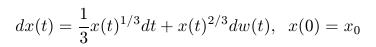
- Ukážte, že funkcia
je jej riešením.
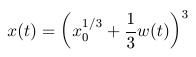
- Nájdite ďalšie riešenie tejto rovnice v prípade, že x(0)=0.
- Ukážte, že funkcia
- Ukážte, že proces
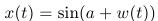 kde
kde 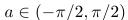 je daná konštanta,
vyhovuje stochastickej diferenciálnej rovnici
ktorá má byť splnená pre časy t vyhovujúce nerovnosti
je daná konštanta,
vyhovuje stochastickej diferenciálnej rovnici
ktorá má byť splnená pre časy t vyhovujúce nerovnosti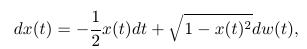 Kde ste pri dôkaze využili toto ohraničenie na čas t?
Kde ste pri dôkaze využili toto ohraničenie na čas t?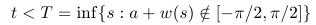
Ukážka priebehu procesu a intervalu jeho existencie pre a=1/2: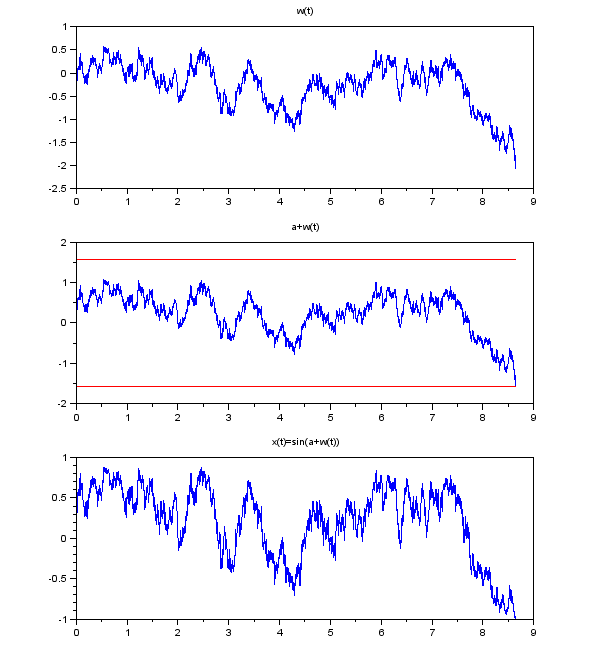
- Nájdite riešenie stochastickej diferenciálnej rovnice
Návod: Je to špeciálny prípad geometrického Brownovho pohybu.
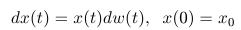
- Použitím substitúcie
nájdite riešenie stochastickej diferenciálnej rovnice
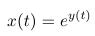
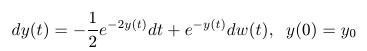
-
Banka modeluje výmenný kurz USD/EUR, označme ho C, geometrickým Brownovym pohybom.
Všimnime si, že potom 1/C je výmenný kurz EUR/USD.
Pobočka banky v eurozóne potrebuje pre svoje výpočty očakávanú hodnotu výmenného kurzu USD/EUR o rok. Použitím modelu banky dostane výsledok, že je to a USD za 1 EUR. Pobočka v USA zasa pre očakávanú hodnotu výmenného kurzu EUR/USD dostane b EUR za 1 USD. Dokážte, že súčin ab je väčší ako 1.
Cvičenia z finančných derivátov, 2014
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/