:: Delta opcie ::

• Derivácia ceny opcie podľa ceny akcie, rovná sa N(d₁)
• Pri odvodení Black-Scholesovho vzorca vystupuje ako počet akcií, ktoré kúpime pri hedžovaní jednej predanej opcie a nazýva sa delta opcie.
• Takémuto hedžovaniu opcií sa hovorí delta hedžing.

:: Cvičenia (1) ::

1. Koľko akcií musíme mať v portfóliu pri delta hedžingu, ak
   • sme vypísali 1000 call opcií s expiračnou cenou 25 USD a expiráciou o pol roka,
   • sme vypísali 1000 put opcií s expiračnou cenou 20 USD a expiráciou o štvrť roka,
   • sme kúpili 1000 call opciís expiračnou cenou 30 USD a expiráciou o rok,
   • sme kúpili 1000 put opcií s expiračnou cenou 20 USD a expiráciou o mesiac,
   ak dnešná cena akcie je 20 USD, volatilita je 0.3 a úroková miera je pol percenta?
   
   
2. Na nasledujúcom obrázku sú zobrazené delty troch call opcií v závislosti od ceny akcie. Tieto opcie sa líšia expiráciou: o 1 deň, o pol roka, o 2 roky. Ostatné parametre sú rovnaké. Priraďte tieto expirácie grafom na obrázku.
   
   
   
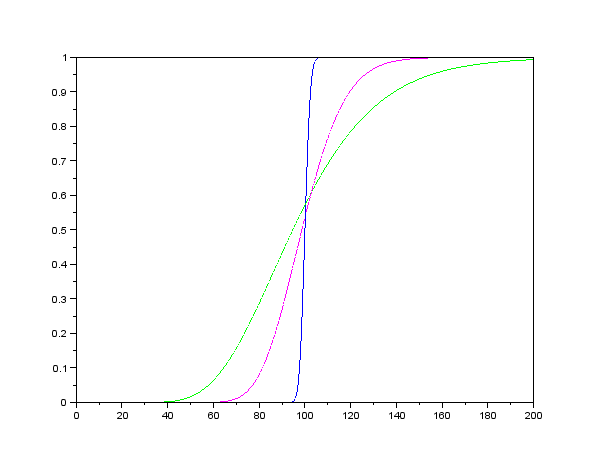
3. K čomu konverguje delta call opcie, ak čas zostávajúci o expirácie ide do nuly a ak ide do nekonečna? Od čoho to závisí? Na základe obrázka a interpretácie delty sformulujte hypotézu a dokážte ju.
   
   
   
4. Delta pre jednoduché deriváty.
   1. Ako vyzerajú riešenia Black-Scholesovej PDR pre koncovú podmienku S a pre koncovú podmienku c (kde c je konštatna)? Čomu sa rovná ich delta a akú má tento výsledok interpretáciu?
   2. Uvažujme Black-Scholesovu rovnicu na akciu s dividendami. Ako sa zmení riešenie PDR pre koncovú podmienku S a príslušná delta? Interpretujte finančne.

:: Cvičenia (2) - ostatné parametre citlivosti ::

1. Príklad z prednášky: závislosť delty od volatility, téma Black-Scholes III, slajd 15
   1. Graficky znázornite závislosť delty od volatility pre rôzne opcie.
   2. Explicitne vypočítajte DdeltaDvol a určte jej znamienko. Čo sa dá na základe vzorce očakávať pre opciu, ktorá je "deep out of the money", ako sa spomína v článku? Porovnajte s numerickými výpočtami a grafmi.
   
   
2. Príklad z prednášky: "cash or nothing" opcia, téma Black-Scholes III, slajd 12-14
   1. Odvoďte cenu tejto opcie podľa Black-Scholesovho vzorca.
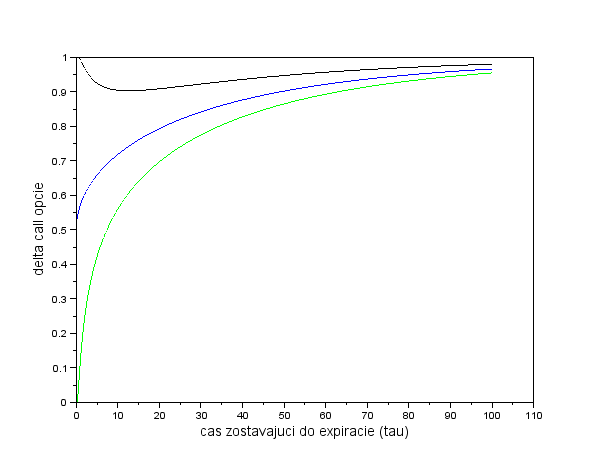
   2. Uvažujme ďalší z parametrov citlivosti - závislosť od času. Odvoďte vzťah pre jeho výpočet, znázornite graficky (priebeh v závislosti od ceny akcie, pre niekoľko časov zostávajúcich do expirácie) a interpretujte.

:: Ďalšie príklady na precvičenie ::

1. Delta pre put opcie. Vypočítajte deltu put opcie. Nakreslite graf jej závislosti od aktuálnej ceny akcie. Vysvetlite priebeh tohto grafu - znamienko, monotónnosť, priebeh pre tau blízke nule.
   
   
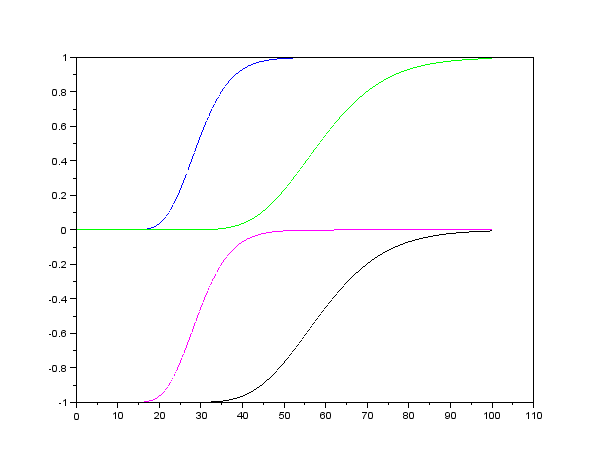
2. Na nasledujúcom obrázku sú zobrazené delty štyroch call opcií v závislosti od ceny akcie: call opcia s E=30, put opcia s E=30, call opcia s E=60, put opcia s E=60. Ostatné parametre sú rovnaké. Priraďte opcie grafom na obrázku.
   
   
   
3. Uvažujme opciu, ktorá vyplatí 1 USD, ak je cena akcia v čase expirácie medzi dvoma stanovenými hodnotami E₁ a E₂ (inak je jej payoff nulový).
   1. Vypočítajte Black-Scholesovu cenu takejto opcie. Návod: Využite vzťah pre cenu cash or nothing opcie.
   2. Vypočítajte deltu takejto opcie a znázornite jej priebeh v závislosti od ceny akcie. Zopakujte pre rôzne časy zostvajúce o expirácie. Ako vyzerá priebeh pre čas blízky expirácie a prečo?

---