:: European call and put options ::

• European options:
  • European call option - a contract, in which a holder of the option is given a right (but not an obligation) to buy the underlying stock at a predetermined expiration time for a predetermined exercise price E.
  • European put option - a contract, in which a holder of the option is given a right (but not an obligation) to sell the underlying stock at a predetermined expiration time for a predetermined exercise price E.
• Payoff = value at the expiration time, as a function of the underlying stock price
  • call option: max(S-E,0)
  • put option: max(S-E,0)
• Profit = payoff decreased by the discounted option price

:: Remark on option symbols ::

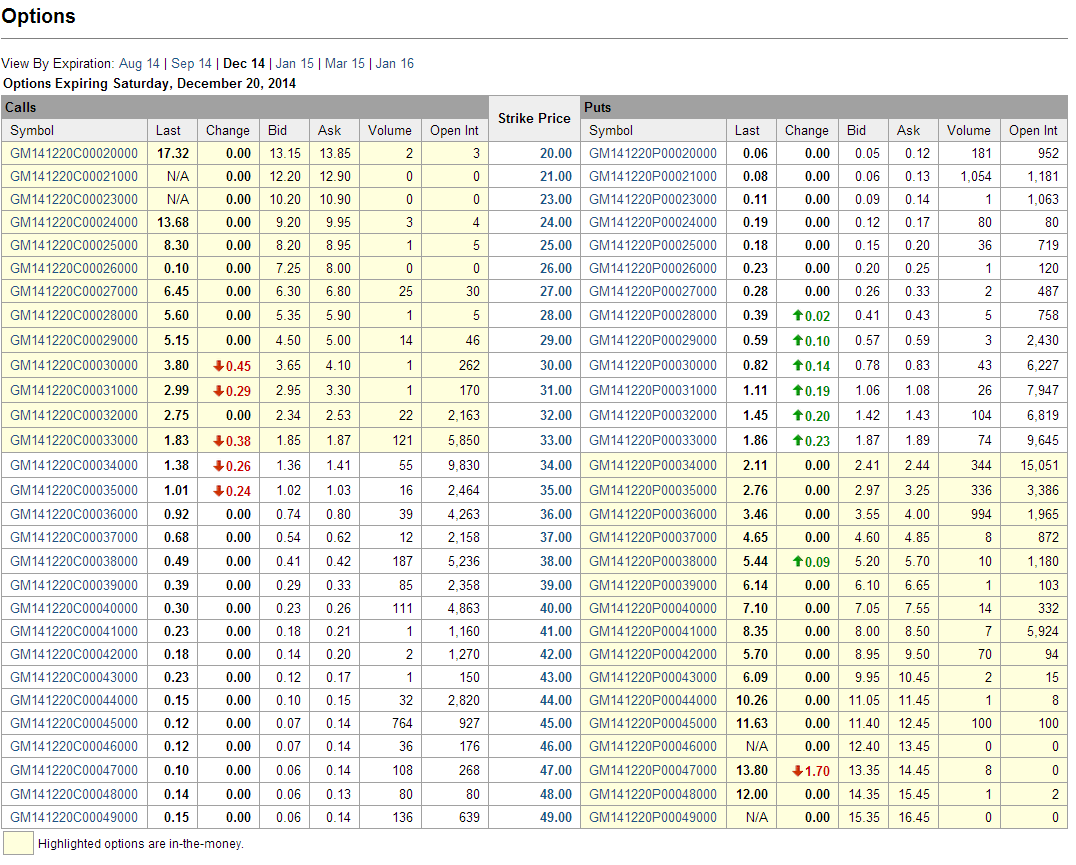
How is it possible that there are several option with the same strike price and the same expiration time?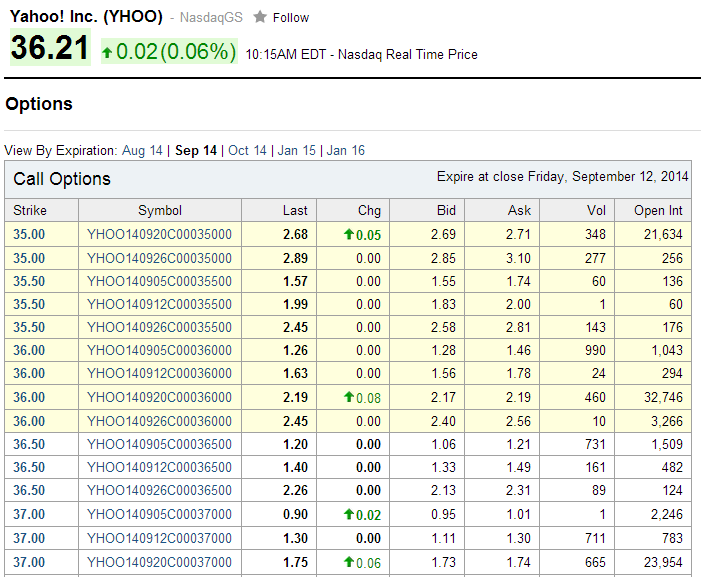

• Options usually expire the third Saturday of a month (and trading end the preceeding Friday), but:
  • not all of them
  • for some stocks there are also so called mini options: normally, options are traded in hundreds, mini option in tens

• Everything cn be deduced from the option symbol:
  • beginning: stock symbol
  • in case of a mini option, the stock symbol is followed by number 7
  • expiration time, coded as YYMMDD
  • option type: call/put, coded as C/P
  • exercise price: decimal point before the last three numbers

:: Payoff and profit diagrams in Scilab ::

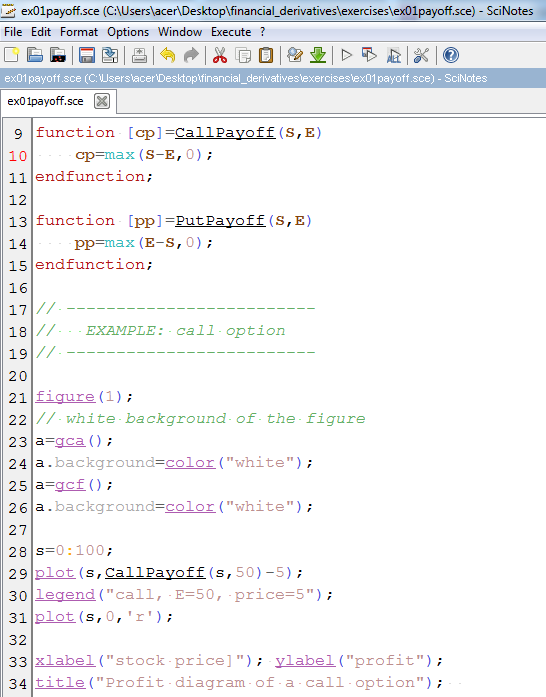
• In Scilab we define function which return payoff of a call option

  function [cp]=CallPayoff(S,E)
     cp=max(S-E,0);
  endfunction; 
  

  and of a put option

  function [pp]=PutPayoff(S,E)
     pp=max(E-S,0);
  endfunction; 
  

• Differences from Matlab:
  • at the end of a function definition: endfunction,
  • functions can be defined at any place of a script

• Now we can plot a payoff diagram and a profit diagram (payoff decreased by the price of the strategy - this means we assume zero interest rate, but since the interest rates are low and the time remaining to expiration is quite short, it does not make a big difference).

[ex01payoff.sce] - Scilab file: definition of the function for computing payoffs of call and put options script for the plot below

Download and run it.

Result: We can choose a format and save the plot - either using Export to (for example to png) ot Vectorial export to (for example to eps).

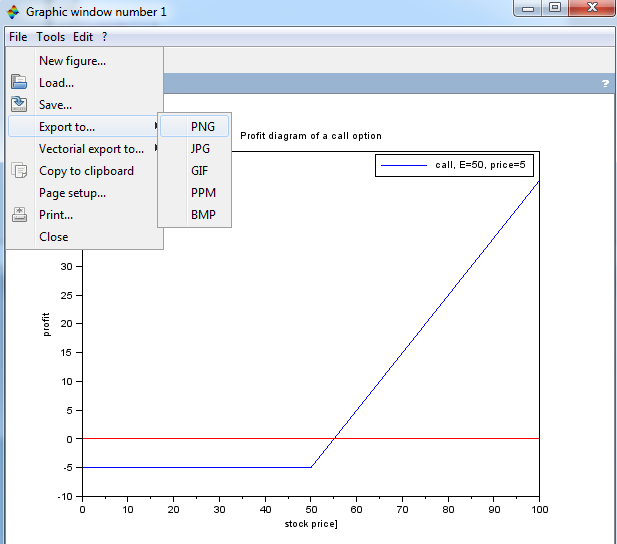
:: Exercises (1) ::

1. Suppose that we have one put option with exercise price 60 USD which costs 7 USD and one call option with the same exercise price which costs 5 USD.
   • Plot payoff and profit diagrams. What expectation about future prices of the stock of the investor is revealed by this strategy?
   • When (for what values of the stock at the expiration time) is the strategy profitable?
   • What is the maximal possible profit? The maximal loss?

:: Moneyness ::

The term characterized the options according to the relation between the current stock price and the strike price of the option.

• ATM (at the money): the stock price equals the strike price
• ITM (in the money): if the option expired today, we would exercise it
• OTM (out of the money): if the option expired today, we would not exercise it

:: Combined strategies ::

Link: http://www.theoptionsguide.com/

• Neutral (non-directional) strategies - they are used if the inverstor doesn't know the direction in which the stock price will move. They differ by the assumption that this move will lead to a small or big change in the price (without specifying the direction of this change).
  • We expect small change - possible strategies are for example:
    • Short straddle: http://www.theoptionsguide.com/short-straddle.aspx
    • Short strangle: http://www.theoptionsguide.com/short-strangle.aspx
    • Long call condor: http://www.theoptionsguide.com/condor.aspx
    • Long call butterfly: http://www.theoptionsguide.com/butterfly-spread.aspx
  • We expect big change - possible strategies are for example:
    • Long straddle: http://www.theoptionsguide.com/long-straddle.aspx
    • Long strangle: http://www.theoptionsguide.com/long-strangle.aspx
    • Short call condor: http://www.theoptionsguide.com/short-condor.aspx
    • Short call butterfly: http://www.theoptionsguide.com/short-butterfly.aspx
• Bearish strategies investor expects the stock price to fall; for example
  • Bear call spread: http://www.theoptionsguide.com/bear-call-spread.aspx
  • Bear put spread: http://www.theoptionsguide.com/bear-put-spread.aspx
• Bullish strategies investor expects the stock price to rise; for example
  • Bull call spread: http://www.theoptionsguide.com/bull-call-spread.aspx
  • Bull put spread: http://www.theoptionsguide.com/bull-put-spread.aspx

:: Real option prices ::

• http://finance.yahoo.com, http://finance.google.com
• We write the code or search the company using its name
• For selected company we display the options. For example:
  
• Option can be bought for ask, sold for bid.

:: Exercises (2) ::

1. Choose one of the strategies listed above and construct its payoff and profit diagrams using real option prices. Under what circumstances will it bring profit?

:: Bounds on option prices ::

• Denote by c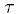(S,,E), p(S,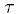,E) prices of a call, resp. put options with strike price E, if the current stock price is S and 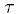is the time remaining to expiration.
• Option prices must satisfy certain inequalities which follow from the no arbitrage requirement. They are proved in the following general way:
  • Consider two portfolios (from stocks, options, bonds).
  • Supoose that at the expiration time, values of the portfolios satisfy the inequality
    P₁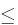 P₂ regardless of the stock price at that time.
  • Then the same inequality must hold also for all the preceeding times.

• Example I. from the lecture: price of a call option is a nonincreasing function of the strike price
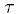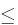  We have shown c(S,,E₁) c(S,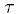,E₂) pre E₂ 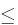E₁
  
  Exercise: Consider the following prices of call options:

  strike price	option price
  10	30
  15	26
  20	27
  25	23
  30	19

  Find an arbitrage - such a strategy that makes profit regardless of the stock price at the expiration time of the options. Plot the profit diagram of your strategy.

  [ex01arbitrage.sce] - Scilab file: data - option prices dependence of option price on the strike price Download the file and plot the profit of your arbitrage strategy.

• Example II.
  Show that c(S,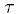,E) is a convex function of the strike price.
  
  Give an example of option prices, for which this property does not hold and used them to find an arbitrage.

:: Practice problems ::

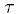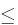1. Prove that p(S,,E₁) p(S,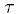,E₂) for E₁ 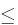E₂ . Construct an example of an arbitrage in a case when this inequality does not hold (with concrete numbers).
   
   
2. Prove that the function p(S,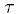,E) is a convex function of the strike price. Construct an example of an arbitrage in a case when this property does not hold (with concrete numbers).
   
   
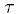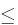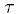3. Prove that S - E exp(-r ) c(S,,E) 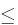S, where r is the interest rate. Construct an example of an arbitrage in a case when this inequality does not hold (with concrete numbers).
   
   
4. Suppose that the interest rate is zero. The stock price is 10 USD and there are call and put options with strike price 12 USD which expire in one month. The call option costs 3 US and the put option costs 4 USD. Find an arbitrage.
   
   
5. Consider the following pair of call and put options: they have the common strike price of 55 USD and they both expire in one year. The stock price is 53 USD and the call price is 0.1 USD higher than the put price. Determine the interest rate.
   
   
6. Find combinations of call and put options which have the following payoffs:
   
   
   
   
   
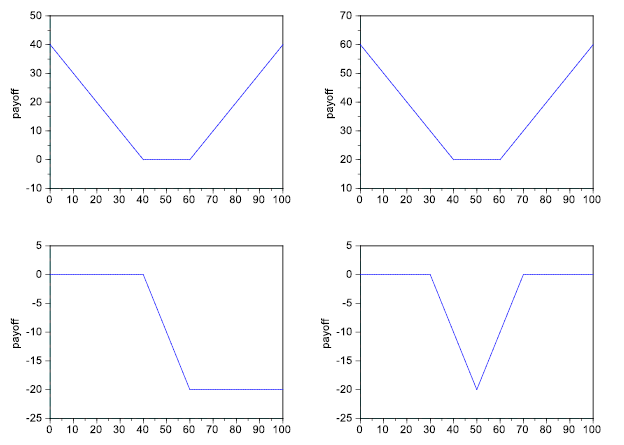
7. [Exam, 2013]
   Sketch the payoff of a strategy consisting of buying a put option with strike price 50 USD and selling a put option with strike price 30 USD. Give an example of such (positive) prices of these options, for which would this strategy lead to an arbitrage opportunity. Construct this arbitrage.
   
   

---