:: Bond prices in a general one-factor short rate model ::

• Recall from the lecture - stochastic differential equation for the short rate:
  
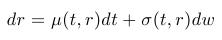
• PDE for the bond prices:
  
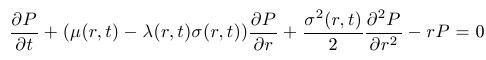
  which depend on the short rate r and time t. The function 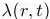is called market price of risk.
• The value of a bond at the time of maturity is equal to unity, hence P(T,r)=1 for all r.
• Bond prices determine interest rates with corresponding maturities:
  

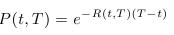
Bond prices in the Vasicek model

• Consider a constant market price of risk, i.e., the function 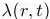is identically equal to a constant .
• Substitution - instead of the time t we will consider the time 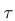remaining to maturity, i.e.,
  
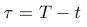
• Solution to the PDE for the bond prices then can be found in a form
  
  where the functions A, B are:
  

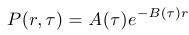
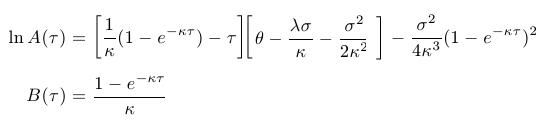
:: Exercises ::

1. Consider parameters of the Vasicek model from the previous exercises session. Select a value of the short rate and plot the term structures for a couple of market price of risk values.
   
   
2. Again, consider parameters of the Vasicek model and select a value of the market price of risk. Plot term structures for different values of the short rate. Prove that as tau approaches infinity, the interest rates with maturity tau converge to
   
   
   
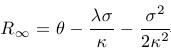
3. Once more, consider parameters of the Vasicek model from the previous exercises session. Suppose that the limit of the term structures is equal to three fourths of the limiting value of the short rate. Compute the market price of risk.
   
   
4. Consider the parameters (i.e., parameters of the short rate and the market price of risk). Find an example of the current value of the short rate, for which the corresponding term structure is not monotone.
   
   
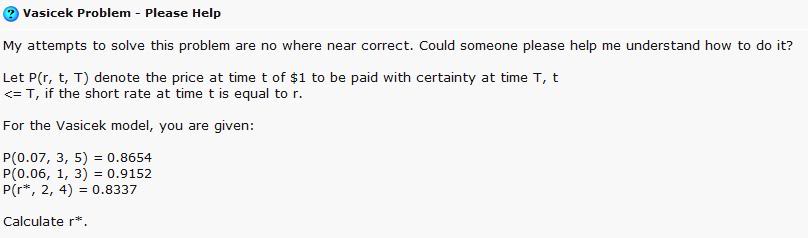
5. Vasicek model problem on an internet discussion forum:
   
   Can you solve it?

---