Black-Scholes formula
:: Scilab files: sci and sce ::
- So far we were using only a few functions which we used in the subsequent code
- Now, we are going to need more functions - prices of a call and a put options (when the stock does not pay dividends and then generalization for continuous dividends), sensitivity parameters (delta, gamma, etc.).
- Scilab uses two types of files - in a sci file we define all the functions (and the file contains only these definitions), sce contains the code using these functions, while in its beginning the functions are loaded by getd(); in this way we load all the functions defined in sci-files in the working directory.
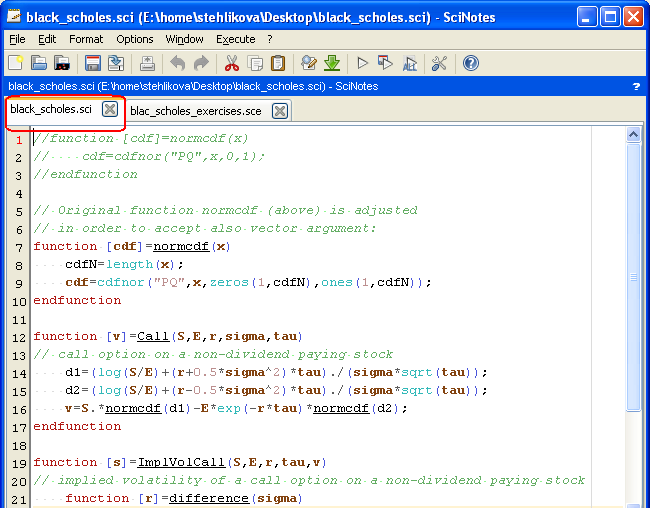
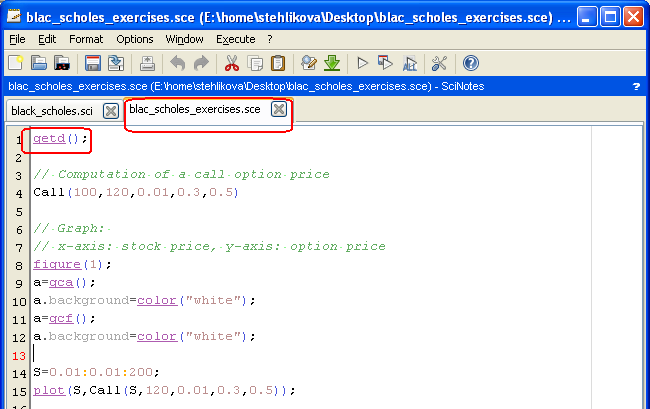
- Download the files: black_scholes.sci (cll option price on a stock that does not pay dividends, implied volatility for such an option) and black_scholes_exercises.sce
:: Price of European call and put options ::
- Example:
Interest rate equals 1 percent. What is the price of a call option with strike price 120 USD and expiration in half of a year, if the current stock price is 100 USD and volatility of the stock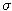 is 0.3?
is 0.3?

- Put option price - can be computed using the put-call parity:
- Consider a portfolio with minus one call option, one put option (written on the same underlying stock, with the same strike price E and with the same expiration price) and one underlying stock.
- Regardless of the stock price, the portfolio has the value E at the time of expiration of the options.
- Therefore, if the time remaining to expiration is
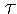 ,the value of the portfolio has to be
,the value of the portfolio has to be 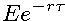 - we know the price of the call, so we can express the value of the put
- we know the price of the call, so we can express the value of the put
- It follows from the linearity of the Black-Scholes PDE, that if the terminal condition of a derivative is a linear combination of call and put options, using the same linear combination of their prices we obtain the price of the derivative.
:: Practice problems ::
- Compute the price of an European call option with expiration in one year, if its strike price is 50 USD, the currect price of the underlying stock is 41 USD and its volatility is 0.3. Interest rate is 0.5 percent.
- From the lecture (motivation for the concept of implied volatility):
Option parameters are given on the previous slides. Compute the historical volatility using the stock prices in 2013 which are given in the file yahoo2013.txt (already in the correct time order). Now, substitute this implied volatility together with the remainding parameters into the Black-Scholes formula and compare the result with the market price of the option.

-
Plot a graph with stock price on the horizontal axis, showing prices of a call option for a couple of different times remaining to expiration.
Sample result:.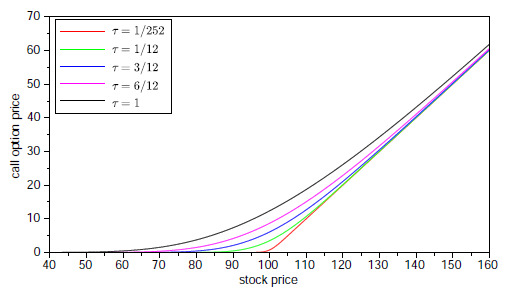
- Write a function which computes the Black-Scholes price of a put option.
Compute the price of a put option with exercise price 105 USD and expiration in 1/4 year, if the current price of the underlying stock is 100 USD and its volatility
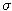 is 0.3. Interest rate is 0.5 percent.
is 0.3. Interest rate is 0.5 percent.
- Construct a combined strategy (choose some from the list given in the first exercise session) for selected parameters. Again, plot a graph
with stock price on the horizontal axis, showing prices of the strategy for a couple of different times remaining to expiration.
Sample result for a butterfly strategy: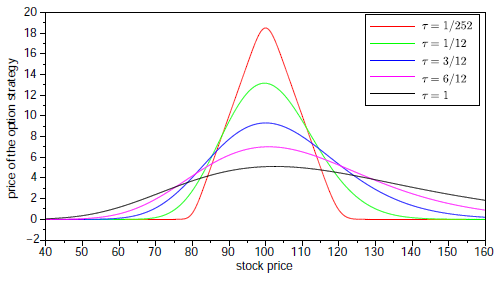
Financial derivatives - exercises, 2014
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://www.iam.fmph.uniba.sk/institute/stehlikova/
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://www.iam.fmph.uniba.sk/institute/stehlikova/