Numerical solution of the Black-Scholes PDE
:: Why a numerical solution ::
- Why are we going to solve the equation numerically, when we have its explicit solution?
- Explicit solution is known to a European call and put options. For other derivatives, such a formula does not have to exist. However, a numerical solution is always possible.
- We firstly use numerical schemes for a case, for which we have an exact solution available. The advantage is that we can check the precision of the results which we obtain.
:: Transformation of the Black-Scholes equation ::
- Black-Scholes equation
- is it a parabolic PDE, which can be transformed to a heat equation with a given initial condition.
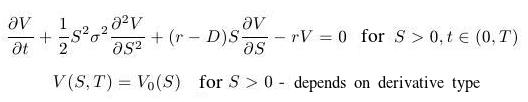
- Transformation of variables
- We have a terminal condition at time T (expiration time), not an initial one. This is solved by transformation
This means that the new variable (instead of original t denoting time) can be interpreted as time remaining to expiration.
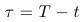
- Variable S (stock price) is positive. Variable, taking all real values, is obtained by taking logarithms. The new variable is therefore
Values of x close to zero correspond to stock prices that are close to the exercise price of the option. Negative value of x correspond to stock prices lower than the exercise price; positive values of x correspond to stock prices higher that the exercise price. It would be sufficient to take a logarithm of the price, but - as we will see later - this will be more convenient from a numerical point of view.
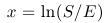
- We have a terminal condition at time T (expiration time), not an initial one. This is solved by transformation
- Transformation to heat equation
- The equation, obtained using the trasformations above, is a parabolic equation, already with constant coefficients. This equation can be transformed to a heat equation by means of a transformation
where the constants are determined in such a way that the transformation leads to a heat equation. The correct choice of the constants is:
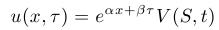 Leads to
Leads to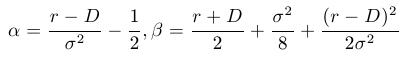
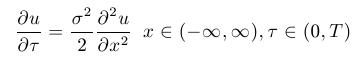
- The equation, obtained using the trasformations above, is a parabolic equation, already with constant coefficients. This equation can be transformed to a heat equation by means of a transformation
- Transformation of the terminal condition:
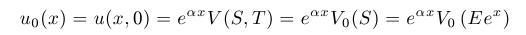
- By solving this heat equation and doing backwards transformations we obtain explicit Black-Scholes formulae, which we used earlier. However, now we want to solve this PDE numerically.
:: Discretization ::
- Variable x is from an unbounded interval, it attains values from minus infinity to plus infinity. Numerically we are going to solve the problem for x from a bounded interval [-L, L], where L is a sufficiently large number.
Note that this interval [-L, L] is not changed when considering an option with another exercise price. The suitable grid points S are obtained thanks to the transformation x = ln(S/E) which we have used instead of a simple logarithmic transformation x = ln(S).
We need to impose boundary conditions for x = -L and x = L. These value of x correspond to stock prices which are very small, close to zero (the case of x = -L) and prices which are very high and approach infinity (the case of x = L). For these limiting values we will use the following approximations:
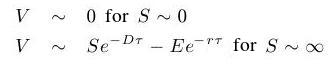
- Further, we have to discretize the heat equation. There are two basic possibilities:
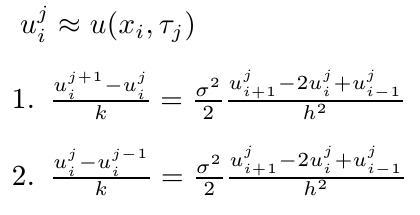
The first approach (explicit scheme) seems to be easier. We have an initial condition. Using these values, we compute the second time level. These are used to compute the next time level, etc. However, to ensure a convergence of the method, a certain condition on time and space steps is required. The condition may practically lead to a necessity of using a very small time step - because of a convergence, not because that we actually need the solution in so many close times.
The second approach (implicit scheme) leads to solving a system of linear equations on each time level.
:: Implicit scheme for a call option ::
-
We choose option parameters:
E = 50; // exercise price r = 0.04; // interest rate D = 0.12; // dividend rate sigma = 0.4; // volatility
- We choose the parameter L which defines the space domain, on which we will compute a numerical solution:
L = 2;
and parameters of the partitions:// space variable n = 20; h = L/n; // time variable T = 1; m = 12; k = T/m;
- Constants needed for the transformation of the equation:
alpha = (r-D)/(sigma^2) - 0.5; beta = (r+D)/2 + (sigma^2)/8 + ((r-D)^2)/(2*sigma^2);
- Boundary conditions for the transformed equation:
// x = -L, i.e., price close to zero function [phi]=phi(tau) phi=0; endfunction // x = L, i.e., price close to infinity function [psi]=psi(tau) psi=E*exp(alpha*L + beta*tau).*(exp(L - D*tau) - exp(-r*tau)); endfunctionand the initial condition:// initial condition function [u0]=u0(x) u0=E*exp(alpha*x).*max(0, exp(x)-1); endfunction
- We create a matrix, to which we will instert our numerical solution:
sol = zeros(2*n + 1,m+1);
and grid points in time and in space:x = -L:h:L; tau = 0:k:T;
Your task: Insert the boundary conditions and the initial condition into the matrix.
- To compute each of the time levels, we need to solve a system of linear equations. Now we define the variables which appear in the tridiagonal matrix of this system:
a = -0.5*(sigma^2)*k/(h^2); // alongside the diagonal b = 1 - 2*a; // on the diagonal
When computing the first time level (the values at time k), we have the following right hand side:rhs = sol(2:2*n,1)'; rhs(1) = rhs(1) - a*phi(k); rhs(2*n-1) = rhs(2*n-1) - a*psi(k);
Firstly, we will use the Gauss-Seidel method to solve this system of equations.You can use the function defined in the file gs.sci:
// ----------------------------------------------------------- // Gauss-Seidel method // for solving a special symmetric tridiagonal system // ----------------------------------------------------------- // // gs(a,b,rhs,v0,eps) // // 3-diagonal matrix with: // a - above and below the diagonal // b - on the diagonal // // rhs - right hand side of the system - a column vector // v0 - initial interation - a column vector // // eps - criterion for ending the iterations: norm(Av-rhs)<=eps // // v - aproximation of the solution (rewritten in the interations) function [v] = gs(a,b,rhs,v0,eps) // matrix A pom = length(v0); A(1, 1) = b; for i = 2 : pom A(i, i) = b; A(i, i - 1) = a; A(i - 1, i) = a; end; // loop until the condition norm(Av-ps)<=eps is satisfied v = v0; while norm(A*v - rhs) > eps v(1) = (rhs(1) - a*v(2))/b; for i = 2:pom-1 v(i) = (rhs(i) - a*(v(i-1) + v(i+1)))/b; end v(pom) = (rhs(pom) - a*v(pom - 1))/b; end; endfunction
Your tasks:- Compute the solution on the first time level and insert it into the solution matrix (as the initial approximation you can tke the values from the previous time level; choose a criterion for stopping iterations)
- Transform the solution into the solution of the Black-Scholes equation.
- Write a loop to compute the solution for each time level.
- Compare with the exact values from the Black-Scholes formula.
A sample output: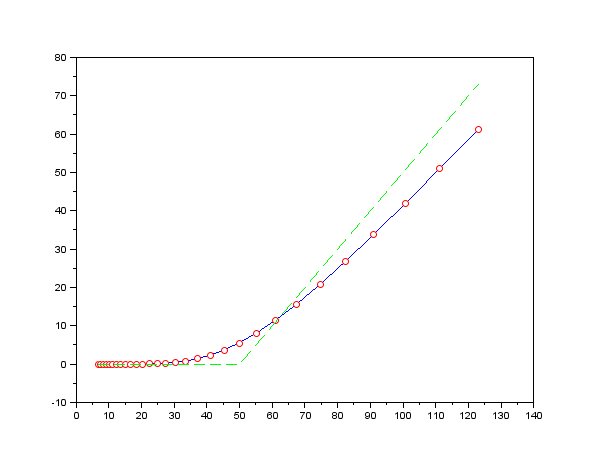
:: SOR method ::
- Adjust the function gs to create a new function sor, which has one additional parameter omega and uses successiv over relaxation (SOR) method to numerically compute solution to the same system of equations. Then, use it to find numerical values of option prices.
Note: The only change in the main code will be calling the function sor instead of the function gs.
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://www.iam.fmph.uniba.sk/institute/stehlikova/