Lelandov model (zahrnutie transakčných nákladov)
:: Lelandov model (zahrnutie transakčných nákladov) ::
- Lelandov model (Hayne E. Leland: Option Pricing and Replication with Transactions Costs, 1985)
- Bid a ask cena akcie: Sbid, Sask - definujeme
- S=(Sbid + Sask)/2
- c=(Sask - Sbid)/S
- Transakčné náklady na jednu transakciu: (c/2)S
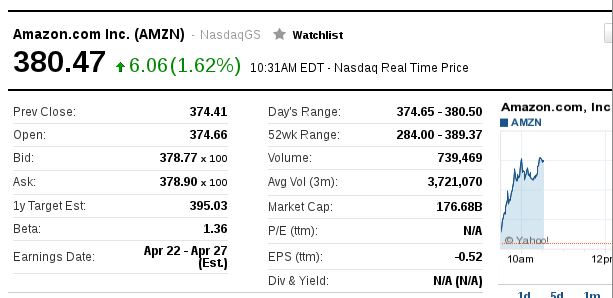
- Aké by malo byť c? Zrátajme si na ukážku, čomu sa rovná pre
akciu AMZN:
- PDR pre ceny derivátov:
- Replikačné portfólio v Black-Scholesovom modeli: 1 opcia,
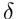 akcií (podľa delta hedžingu) spojité obchodovanie.
akcií (podľa delta hedžingu) spojité obchodovanie.
- V prípade transakčných nákladov: 1 opcia,
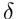 akcií (podľa delta hedžingu), portfólio meníme v intervaloch dĺžky
akcií (podľa delta hedžingu), portfólio meníme v intervaloch dĺžky 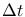 , počet transakcií je
, počet transakcií je 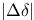
- Zmena hodnoty portfólia:
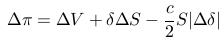
- Dostaneme PDR:
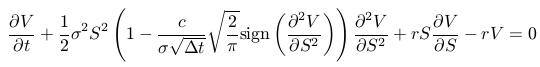
- Replikačné portfólio v Black-Scholesovom modeli: 1 opcia,
- Pre call a put opciu:
- Definujeme Lelandovo číslo
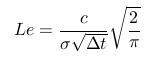
- Pre Lelandovo číslo z intervalu (0,1) dostávame cenu call,
resp. put opcie pomocou Black-Scholesovho vzorca s upravenou
volatilitou:
Dôkaz: dosadíme do rovnice, využujeme, že cena call a put opcie v Black-Scholesovom modeli je konvexná funkcia premennej S.
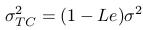
- Definujeme Lelandovo číslo
:: Cvičenia (1) ::
- Napíšte funkciu, ktorá počíta hodnotu Lelandovho čísla (v závislosti
of volatility akcie, konštanty c, intervalu medzi dvoma zaisteniami
portfólia). Pre zvolené hodnoty parametrov overte podmienku, že Lelandovo číslo
je z intervalu (0,1).
-
Pre prípustné hodnoty parametrov vypočítajte hodnotu call a put opcie
za prítomnosti transakčných nákladov (parametre: cena akcie, expiračná
cena, volatilita, čas do expirácie, úroková miera, konštanta c, interval
medzi dvoma zaisteniami portfólia). Napíšte funkciu, ktorá bude pre zadané hodnoty počítať cenu call a put opcie v Lelandovom modeli.
- Zvoľte si parametre akcie a opcie, a úrokovú mieru - vstupy potrebné do Lelandovho modelu. Ako závisí Lelnadovho čísla od času medzi dvoma zmenami portfólia. Aké časy sú prípustné? Pre niekoľko z nich vypočítajte cenu opcie a porovnajte ju s Black-Scholesovou cenou. Aký vplyv na cenu má zvolený čas medzi dvoma zmenami portfólia?
:: Modelovanie bid-ask spreadov pomocou Lelandovho modelu ::
- Cenu z predchádzajúceho odvodenia môžeme považovať za ponuku na kúpu opcie.
- Na prednáške sme odvodili aj ponuku na predaj - cenu call, resp. put opcie znovu dostaneme pomocou Black-Scholesovho vzorca, pričom upravená volatilita je:
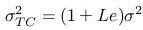
- To znamená, že upravené volatility sú:
a rozdiel medzi ask a bid cenou je
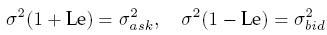
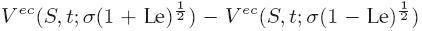
- Tieto výsledky nám umožňujú odhadnúť parametre modelu z dát:
- Vypočítame implikované bid a ask volatility
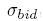 a
a 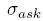 z bid a ask ceny opcie:
z bid a ask ceny opcie:
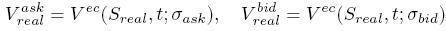
- Riešením sústavy rovníc vypočítame parametre
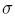 (implikovaná volatilita), Le:
(implikovaná volatilita), Le:
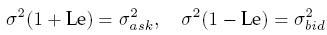
- Z bid a ask ceny akcie vypočítame konštantu c z Lelandovho modelu.
- Nakoniec vypočítame implikovaný čas medzi dvoma prerovnaniami porfólia pri hedžingu opcie:
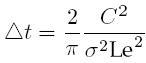
- Vypočítame implikované bid a ask volatility
:: Cvičenia (2) ::
-
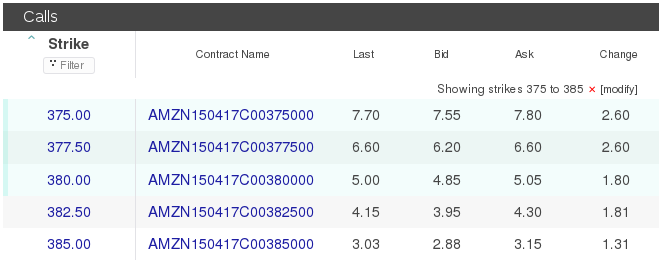
Použite uvedený postup na odhad parametrov Lelandovho modelu pomocou niektorej z
nasledovných call opcií. Dáta sú z 8. 4. 2015.
:: Ďalšie príklady na precvičenie ::
- Implikované parametre v Lelandovom modeli pre put opcie. Postup je rovnký, len potrebujeme funkciu na výpočet implikovanej volatility pre put opcie v Black-Scholesovom modeli.
Zrealizujte tento výpočet pre nasledujúce dáta [písomka, 2014]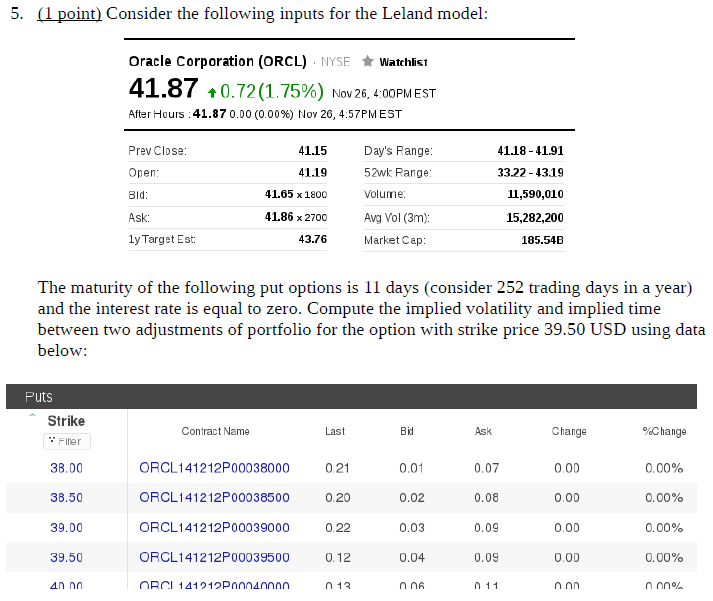
- [Vzorová písomka, 2009]

- [Písomka, 2009]
Išlo o nasledovné dáta:

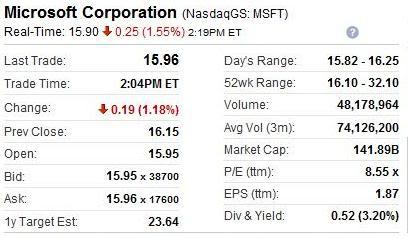
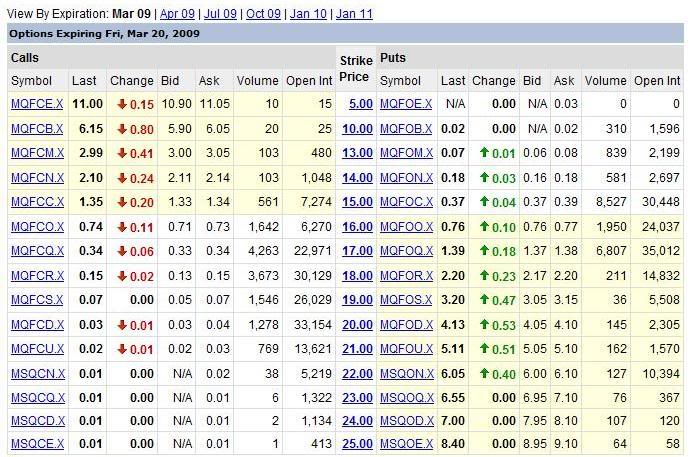
- Uvažujme rozdiel bid a ask ceny opcie ako funkciu ceny akcie S.
(Ostatné parametre - volatilita akcie, parameter c charakterizujúci
transakčné náklady, úroková miera, expiračná cena a čas expirácie opcie -
sú konštantné).
- Znazornite graficky tento rozdiel pre zvolené hodnoty parametrov.
- Pre akú cenu akcie je tento rozdiel maximálny? Vypočítajte analyticky pre všeobecné hodnoty parametrov.
Cvičenia z finančných derivátov, 2014
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/