:: Jednofaktorový short rate model ::

• Úrokové miery - napríklad Euribor:
  
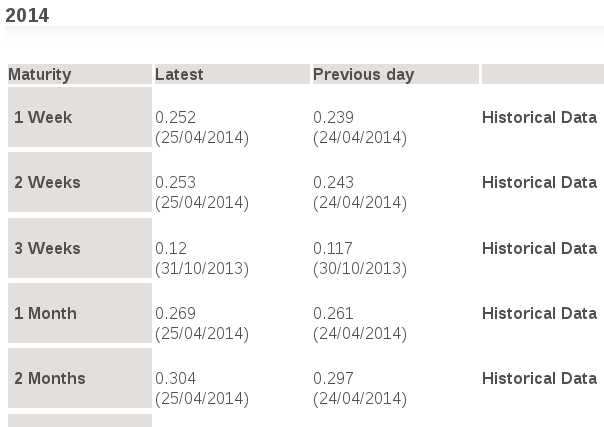
• Short rate - okamžitá úroková miera, aproximuje sa úrokovou mierou s krátkou splatnosťou
• Okamžitá úroková miera sa modeluje stochastickou diferenciálnou rovnicou:
  
  teda trend vo vývoji úrokovej miery + náhodné fluktuácie okolo trendu
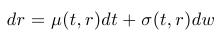
• Jednofaktorový model - jedna stochastická diferenciálna rovnica pre r, t. j. jeden zdroj náhodnosti vo vývoji okamžitej úrokovej miery (jeden Wienerov proces).

:: Vašíčkov model :::

• Stochastická diferenciálna rovnica pre okamžitú úrokovú mieru:
  
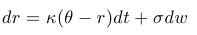
• Vlastnosť mean-reversion (priťahovanie k dlhodobej hodnote, k limitnej hodnote) - pre strednú hodnotu platí:
  
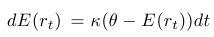
• Volatilita je konštantná, nezávisí teda od aktuálnej hodnoty úrokovej miery

:: Pravdepodobnostné rozdelenie úrokových mier ::

• Na prednáške: podmienené rozdelenie úrokovej miery, ak poznáme jej hodnotu r₀ v čase 0 - je to normálne rozdelenie 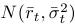s parametrami
  
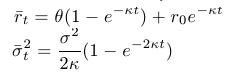
• Znalosť tohoto rozdelenia nám umožňuje:
  • Vygenerovať realizáciu procesu pre zadané parametre a začiatočnú hodnotu úrokovej miery.
  • Odhadovať parametre procesu z dát.
• Upozornenie: V literatúre sa požívajú rôzne označenia pre lineárnu funkciu driftu, treba si vždy pozrieť, s akým driftom sa pracuje.

::Cvičenia (1) ::

1. Článok Athanasios Episcopos: Further evidence on alternative continuous time models of the short-term interest rate. Journal of International Financial Markets, Institutions and Money 10 (2000) 199-212, kde autor odhadoval modely úrokových mier. Všeobecný model, ktorým sa zaoberal, je
   
   Zoberieme parametre pre Nový Zéland:
   
   
   
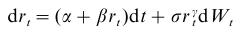
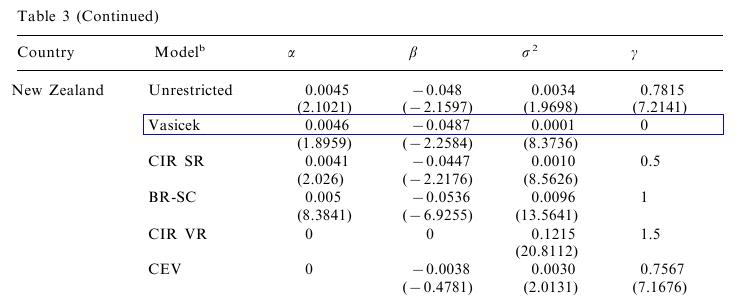
   • Preveďte tieto parametre tak, aby sme proces mali vyjadrený ho pomocou parametrov 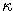, , 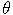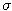. Predpokladajte, že dnešná hodnota úrokovej miery je 4.5 percenta a vygenerujte trajektóriu jej ďalšieho vývoja pomocou presného podmieneného rozdelenia. Zakreslite do tohto grafu aj strednú hodnotu úrokovej miery.
     
     
   • Predpokladajte, že dnešná hodnota úrokovej miery je 4.5 percenta. Aká je stredná hodnota úrokovej miery o týždeň, o mesiac a o rok? Zostrojte pre tieto úrokové miery intervalové odhady (stredná hodnota +/- 2*štandardná odchýlka).
     
     
   • Aké je limitné rozdelenie úrokovej miery? Nakreslite graf hustoty tohto limitného rozdelenia. Doplňte do grafu hustoty rozdelenia úrokovej miery o mesiac, o rok, ... - tak, aby ste videli konvergenciu týchto hustôt k limitnej hustote.

      // hustota N(m,s2), upravte pre vektorovy argument x 
     function [f]=f(x,m,s2)
         f=exp((x-mi)^2/(2*s2))/sqrt(2*%pi*s2);
     endfunction
     

     
     

:: Metóda maximálnej vierohodnosti na odhadovanie parametrov ::

• Podmienené rozdelenie úrokových mier je normálne, preto funkcia vierohodnosti je súčin hustôt normálnych rozdelení. Odhady parametrov sa dajú explicitne vyjadriť.
  
  
• Damiano Brigo, Fabio Mercurio: Interest Rate Models - Theory and Practice. Second Edition. Springer, 2007. Kapitola 3.1.2, str. 61-62:
  
  [books.google.com]
  
  
• Môže sa vám hodiť nasledujúci skript, v ktorom sú prepísané tieto vzorce pre odhady: [vasicekMLE.sce]

:: Cvičenia (2) ::

1. Ako z týchto odhadov dostaneme odhady parametrov 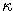, , 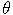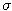? Odvoďte príslušnú transformáciu. Odhadnite tieto parametre pre dáta [euro2014q1.txt] (európske úrokové miery v prvom kvartáli 2014).

:: Testovanie štatistických hypotéz o parametroch ::

1. Podľa zadania v [cv9b.pdf]

:: Ďalšie príklady na precvičenie ::

1. Uvažujme exponenciálny Vašíčkov model, v ktorom sa okamžitá úroková miera modeluje ako:
   
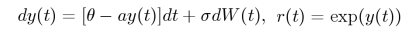
   • Nájdite odhady parametrov pre dáta [euro2014q1.txt] (návod: pre zlogaritmované dáta viete použiť postup pre odhadovanie parametrov klasického Vašíčkovho modelu)
   • Spravte predikcie pre nasledujúci štvrťrok a porovnajte ich s predikciami z Vašíčkovho modelu. Nakreslite priebeh oboch predikcií do jedného obrázku a porovnajte ich so skutočným vývojom úrokovej miery v druhom štvrťroku.
   
   
2. Uvažujme Dothanov model, v ktorom sa okamžitá úroková miera modeluje ako:
   
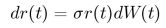
   • Nájdite podmienené rozdelenie úrokovej miery (pri jej danej dnešnej hodnote).
   • Použite toto rozdelenie na konštrukciu funkcie vierohodnosti pre dáta [euro2014q1.txt]. Nakreslite jej priebeh pre vhodný rozsah premennej sigma a nájdite maximum.
   • Pre odhad získaný v predchádzajúcom bode a zostojte hustotu rozdelenia úrokovej miery v polovici roka 2014.
   • Porovnajte túto hustotu s hustotami získanými z odhadovana Vašíčkovho a exponenciálneho Vašíčkovho modelu.
   
   
3. Zopakujte predchádzajúce výpočty s aktuálnymi dátami. Stiahnite si dáta úrokovej miery (napr. 3M treasury bills, Euribor s krátkou dobou splatnosti a pod.) zo zvoleného časového intervalu. Zobrazte ich vývoj. Zdroje dát - napríklad:
   • Federal Reserve Statistical Release
   • Euribor
   • Bank of Canada

---