:: European call and put options ::

• European options:
  • European call option - a contract, in which a holder of the option is given a right (but not an obligation) to buy the underlying stock at a predetermined expiration time for a predetermined exercise price E.
  • European put option - a contract, in which a holder of the option is given a right (but not an obligation) to sell the underlying stock at a predetermined expiration time for a predetermined exercise price E.
• Payoff = value at the expiration time, as a function of the underlying stock price
  • call option: max(S-E,0)
  • put option: max(E-S,0)
• Profit = payoff decreased by the discounted option price

:: Remark on option symbols ::

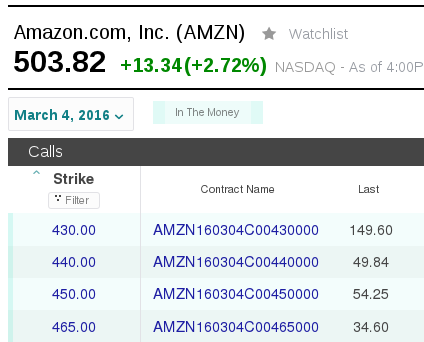
• Example of options prices:
  
• What can be deduced from the option symbol:
  • beginning: stock symbol
  • in case of a mini option (unit of trading is 10, normally 100), the stock symbol is followed by number 7
  • expiration time, coded as YYMMDD
  • option type: call/put, coded as C/P
  • exercise price: decimal point before the last three numbers

:: Payoff and profit diagrams in R ::

• We define function which returns payoff of call and put options:
  
• Now we can plot a payoff diagram and a profit diagram (payoff decreased by the price of the strategy - this means we assume zero interest rate, but since the interest rates are low and the time remaining to expiration is quite short, it does not make a big difference).
  
  Questions from the lecture (slide 23):
  
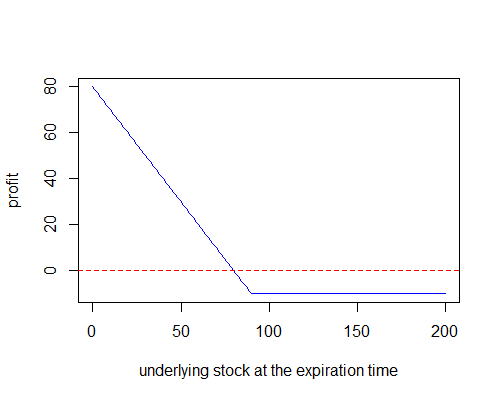
• Replicate the graph above.
• Explain, why is it more convenient to use the function pmax instead of max in the definitions of callPayoff and putPayoff.

:: Exercises (1) ::

1. Suppose that we have one put option with exercise price 60 USD which costs 7 USD and one call option with the same exercise price which costs 5 USD. Plot payoff and profit diagrams. When (under what expectation about the stock price behaviour) would you consider this strategy?
   
   
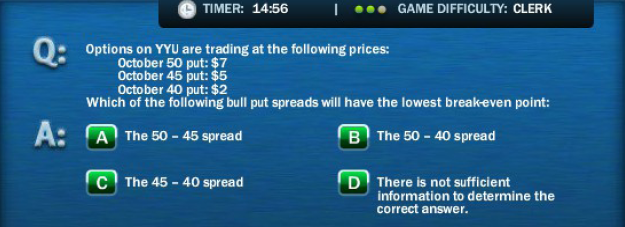
2. The second extra credit assignment will be an online game on the topic of financial derivatives. Some questions deal with option strategies, for example the following one:
   

:: Moneyness ::

The term characterized the options according to the relation between the current stock price and the strike price of the option.

• ATM (at the money): the stock price equals the strike price
• ITM (in the money): if the option expired today, we would exercise it
• OTM (out of the money): if the option expired today, we would not exercise it

:: Combined strategies ::

Link: www.theoptionsguide.com

• Neutral (non-directional) strategies - they are used if the inverstor doesn't know the direction in which the stock price will move. They differ by the assumption that this move will lead to a small or big change in the price (without specifying the direction of this change).
  • We expect small change - possible strategies are for example:
    • Short straddle: http://www.theoptionsguide.com/short-straddle.aspx
    • Short strangle: http://www.theoptionsguide.com/short-strangle.aspx
    • Long call condor: http://www.theoptionsguide.com/condor.aspx
    • Long call butterfly: http://www.theoptionsguide.com/butterfly-spread.aspx
  • We expect big change - possible strategies are for example:
    • Long straddle: http://www.theoptionsguide.com/long-straddle.aspx
    • Long strangle: http://www.theoptionsguide.com/long-strangle.aspx
    • Short call condor: http://www.theoptionsguide.com/short-condor.aspx
    • Short call butterfly: http://www.theoptionsguide.com/short-butterfly.aspx
• Bearish strategies investor expects the stock price to fall; for example
  • Bear call spread: http://www.theoptionsguide.com/bear-call-spread.aspx
  • Bear put spread: http://www.theoptionsguide.com/bear-put-spread.aspx
• Bullish strategies investor expects the stock price to rise; for example
  • Bull call spread: http://www.theoptionsguide.com/bull-call-spread.aspx
  • Bull put spread: http://www.theoptionsguide.com/bull-put-spread.aspx

You can also use Option Strategy Finder on that website to find a strategy that meets your criteria.

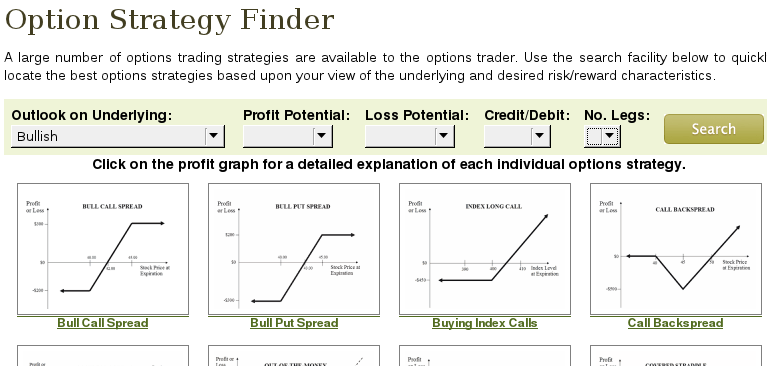
:: Shiny packege for R ::

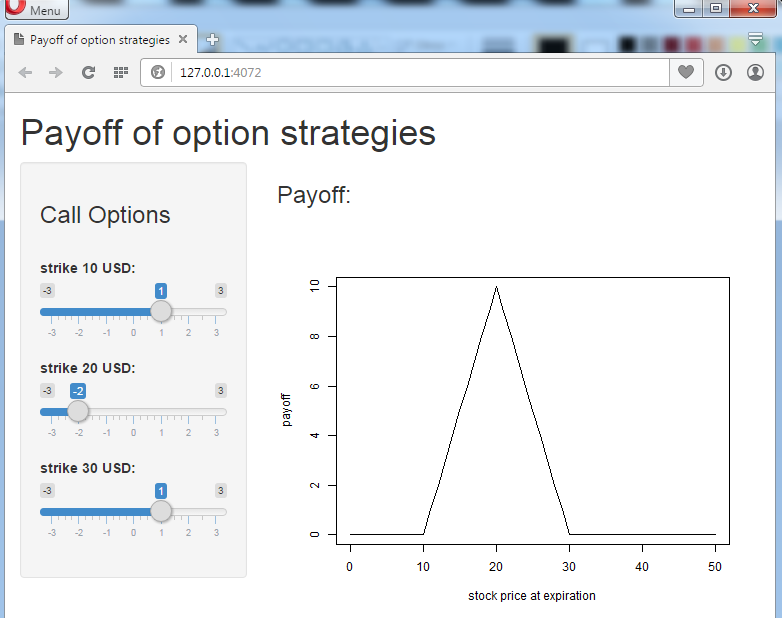
• Example of what can be done using Shiny:
  
• How to run it:
  • Download the files ui.R (user interface) and server.R
  • Put them into one folder.
  • Install shiny package in R studio.
  • Run the Shiny application - click on Run App:
    
  • Construct some option stategy and comment on its payoff. When would you use this strategy?
• How does it work:
  • User interface - file ui.R:
    • In this layout, there are three panels:
      
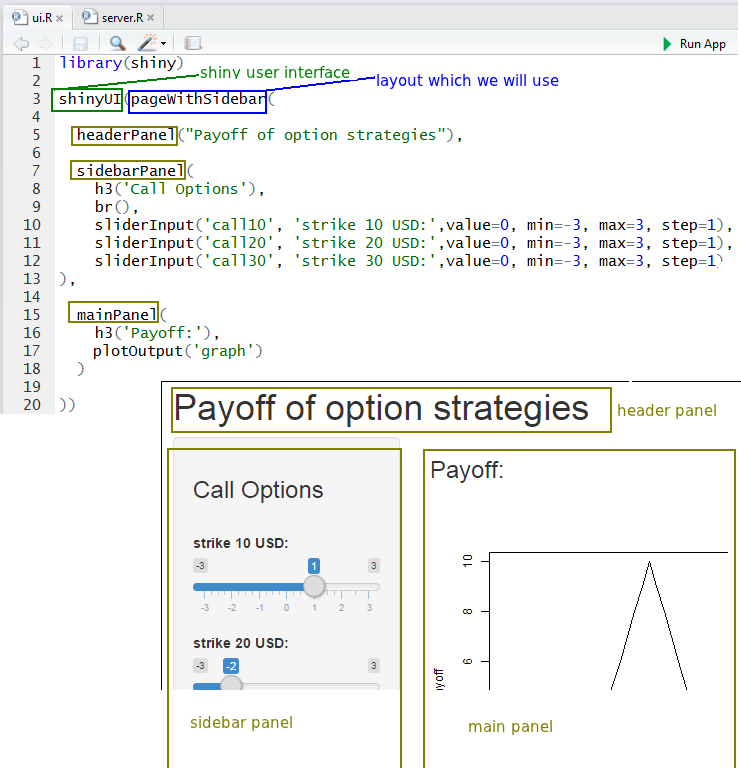
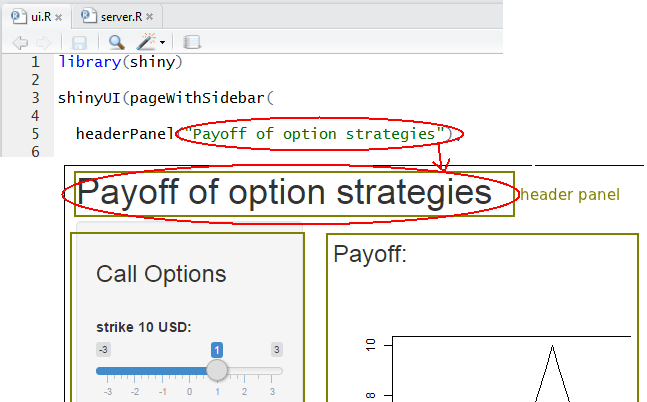
    • For the header panel we specify the title which should be displayed:
      
    • Overview of the side panel:
      
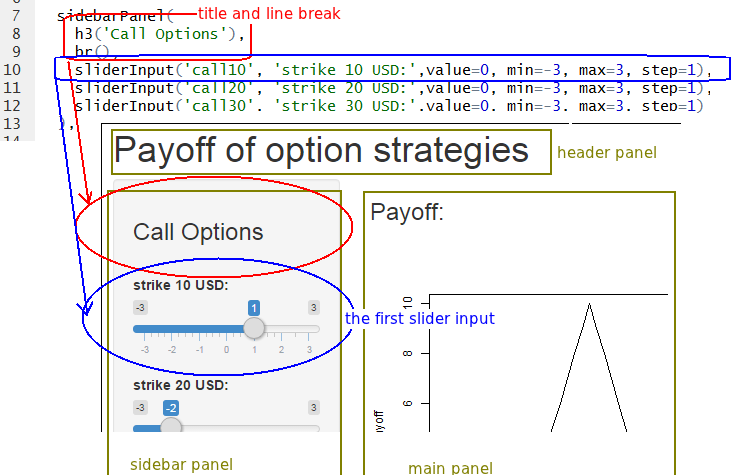
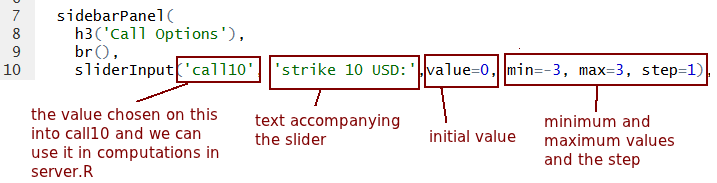
    • And slider input in more detail:
      
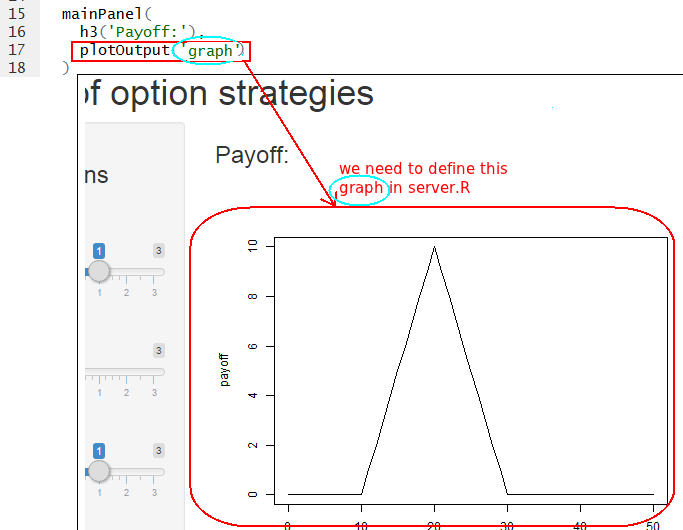
    • Main bar:
      
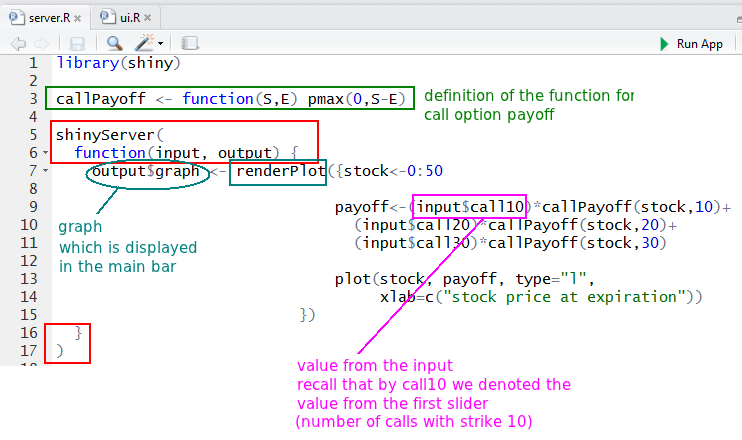
  • server.R:
    

  :: Exercises (2) ::

  1. Add a possibility to use also put options with the same exercise prices. Choose a strategy which uses puts or a combination of calls and puts, and construct its payoff diagram using your Shiny application.

  :: Bounds on option prices ::

  • Denote by c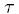(S,,E), p(S,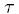,E) prices of a call, resp. put options with strike price E, if the current stock price is S and 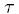is the time remaining to expiration.
  • Option prices must satisfy certain inequalities which follow from the no arbitrage requirement. They are proved in the following general way:
    • Consider two portfolios (from stocks, options, bonds).
    • Supoose that at the expiration time, values of the portfolios satisfy the inequality
      P₁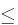 P₂ regardless of the stock price at that time.
    • Then the same inequality must hold also for all the preceeding times.
  • Example from the lecture: We have shown that the price of a call option is a nonincreasing function of the strike price, i.e.,
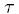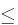    c(S,,E₁) c(S,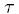,E₂) for E₂ 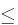E₁

  :: Exercises (3) ::

  1. Consider the following prices of call options:

     strike price	option price
     10	40
     20	35
     30	32
     40	33
     50	30

     Find an arbitrage - such a strategy that makes profit regardless of the stock price at the expiration time of the options. Plot the profit diagram of your strategy.
     
     
  2. Prove that c(S,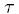,E) 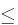S. Construct an example of an arbitrage in a case when this inequality does not hold (with concrete numbers).

  :: Practice problems ::

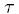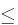  1. Prove that p(S,,E₁) p(S,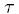,E₂) for E₁ 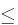E₂ . Construct an example of an arbitrage in a case when this inequality does not hold (with concrete numbers).
     
     
  2. Prove that the function p(S,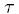,E) is a convex function of the strike price. Construct an example of an arbitrage in a case when this property does not hold (with concrete numbers).
     
     
  3. Prove that the function c(S,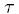,E) is a convex function of the strike price. Construct an example of an arbitrage in a case when this property does not hold (with concrete numbers).
     
     
  4. Prove that S - E exp(-r ) c(S,,E), where r is the interest rate. Construct an example of an arbitrage in a case when this inequality does not hold (with concrete numbers).
     
     
  5. Suppose that the interest rate is zero. The stock price is 10 USD and there are call and put options with strike price 12 USD which expire in one month. The call option costs 3 US and the put option costs 4 USD. Find an arbitrage.
     
     
  6. Consider the following pair of call and put options: they have the common strike price of 55 USD and they both expire in one year. The stock price is 53 USD and the call price is 0.1 USD higher than the put price. Determine the interest rate.
     
     
  7. Find combinations of call and put options which have the following payoffs:
     
     
     
     
     
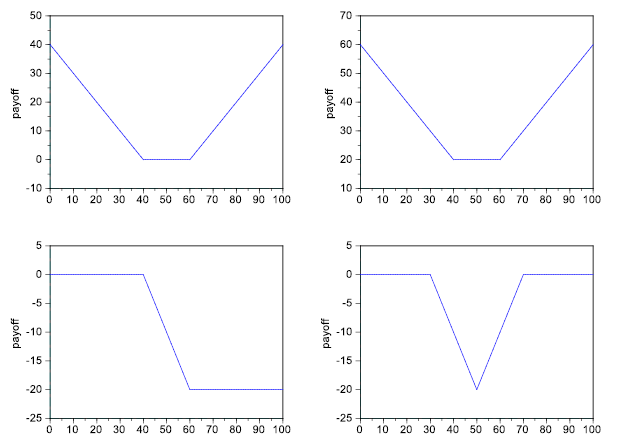
  8. [Exam, 2013]
     Sketch the payoff of a strategy consisting of buying a put option with strike price 50 USD and selling a put option with strike price 30 USD. Give an example of such (positive) prices of these options, for which would this strategy lead to an arbitrage opportunity. Construct this arbitrage.
     
     
  9. [Test I, 2014]
     
     
  
  

  ---

  Financial derivatives - exercises
  Beáta Stehlíková, FMFI UK Bratislava
  
  E-mail: stehlikova@pc2.iam.fmph.uniba.sk
  Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/