:: Black Scholes price of European options ::

• Download black_scholes.R - R file for this exercise
  
  
• Here we have a function which computes the Black-Scholes price of a call option on a stock which does not pay dividends:
  
• Now we can compute for example:
  

:: Exercises (1) ::

1. Compute the price of an European call option with expiration in one year, if its strike price is 50 USD, the currect price of the underlying stock is 41 USD and its volatility is 0.3. Interest rate is 0.5 percent.
   
   
2. Plot a graph with stock price on the horizontal axis, showing prices of a call option for a couple of different times remaining to expiration. Sample result:.
   
   
   
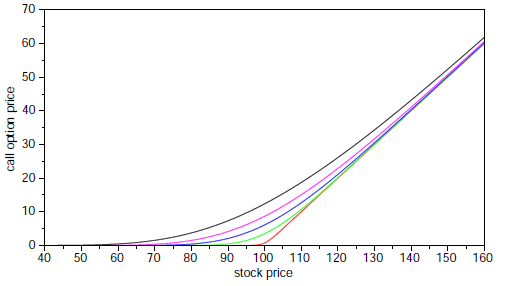
3. Write a function which computes the Black-Scholes price of a put option. Compute the price of a put option with exercise price 105 USD and expiration in 1/4 year, if the current price of the underlying stock is 100 USD and its volatility is 0.3. Interest rate is 0.5 percent.
   
   
4. Implement a computation of implied volatility of a call option written on a stock which does not pay dividends.

:: Delta of an option ::

• Derivative of the option price with respect to the stock price.
• For a call option on a stock that does not pay dividends, it equals N(d₁)
• In the derivation of the Black-Scholes formula it is the number of stocks which we buy to hedge one option that we had written
• This hedging is called delta hedging.

:: Exercises (2) ::

1. How many stocks we need in our portfolio, if
   • we sell 1000 call options with strike price 25 USD and expiration in 1/2 year,
   • we sell 1000 put options with strike price 20 USD a expiration in 1/4 year
   • we buy 1000 call options with strike price 30 USD and expiration in 1 year,
   • we buy 1000 put options with strike price 20 USD and expiration in 1 month,
   the stock price today is 20 USD, its volatility is 0.3 and the interest rate is 0.5 percent?
   
   
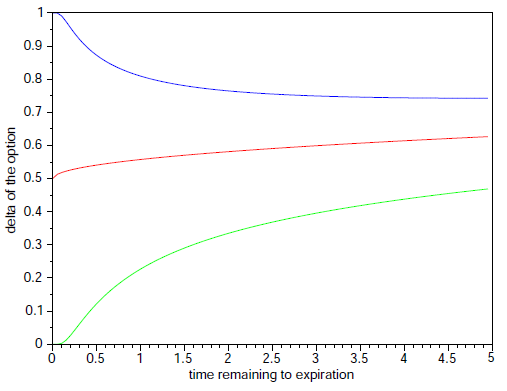
2. The following graph shows deltas of three call options as function of the stock price. These options have different time remaining to their maturity: 1 day, 1/2 year, 2 years. Remaining parameters are the same. Add the maturities to corresponding deltas.
   
   
   
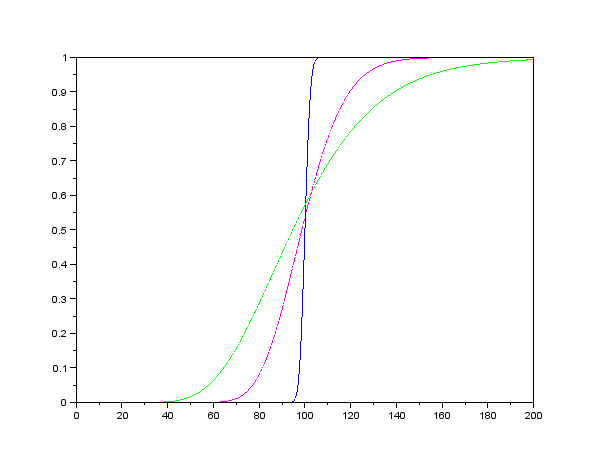
3. What is the limit of the delta, as time remaining to expiration appoaches zero and as it approaches infinity? Based on the plot and interpretation of a delta formulate a hypothesis and prove it.
   
   
   
4. Delta of simple derivatives
   • What are the solutions to the Black-Scholes PDE which satisty the terminal condition S and the terminal condition c (where c is a constant)? What are their deltas and what is the interpretation of these results?
   • Consider the Black-Scholes PDE if the underlying stock pays continuous dividends. What is - in this case - solution to the PDE satisfying the terminal condition S and the corresponding delta? Give a financial interpretation.

:: Exercises (3) - Other measures of sensitivity::

1. Greeks for a binary "cash-or-nothing" option. From the lecture we know the price of a binoary option:
   
   Derive its delta (derivative with respect to stock price) and vega (derivative with respect to volatility) and plot their dependence on stock price for different times. Explain the behaviour of these functions in an intuitive financial way.

:: Practice problems ::

1. Implement computations of:
   • price and delta for call and put options on a stock which pays continuous dividends
   • price and delta for binary "cash-or-nothing" options which pays 1 USD if the stock is below E at expiration and zero otherwise; the underlying stock does not pay dividends
   • implied volatility for call and put options written on a stock which pays contunuous dividends
   
   
2. The following graph shows deltas of four options as functions of the underlying stock price: call option with E=30, put option with E=30, call option with E=60, put option with E=60. The remaining parameters are constant. Add the options to their deltas.
   
   
   
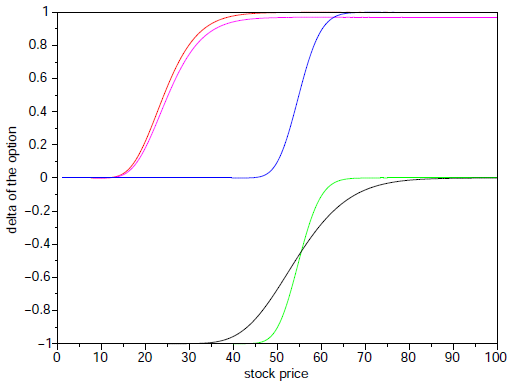
3. Consider an option which pays 1 USD if, at the time of expiration, the stock price is between two predetermined values E₁ and E₂ (otherwise its payoff is zero).
   • Compute the Black-Scholes price of this option. Hint: Use the formula for a cash-or-nothing option.
   • Compute delta of this option and plot its graph as a function of the stock price. Repeat for different times to maturity. What is the behaviour for time close to maturity and why?


4. On quant.stackexchange.com appeared the following question:
   
   The answer beginns with:
   
   • Explain, firstly without computation of concrete numerical values, why should we attempt to look for a counterexample at an ITM option on a stock with high volalility
   • Then, find concrete values of parameters to obtain a counterexample to the claim from the question.
   
   Discussion continued:
   
   • What is the dependence of the price and delta on remaining parameters? Find parameter values which constitute a counterexample with a volatilit equal to 0.3 and an option shich is not so deep ITM.

---

---