Black - Scholes model II.
:: Practice problems ::
- From the lecture:

- Practice exam, 2014/2015:
The code is from Scilab, but it should be easy to understand. The function normcdf computes the cumulative distribution function of a normalized normal distribution.
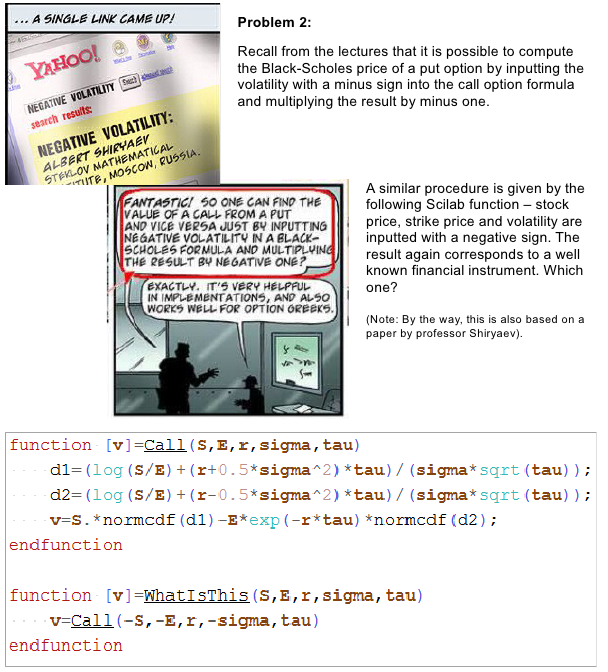
-
Exam, 2014/2015:
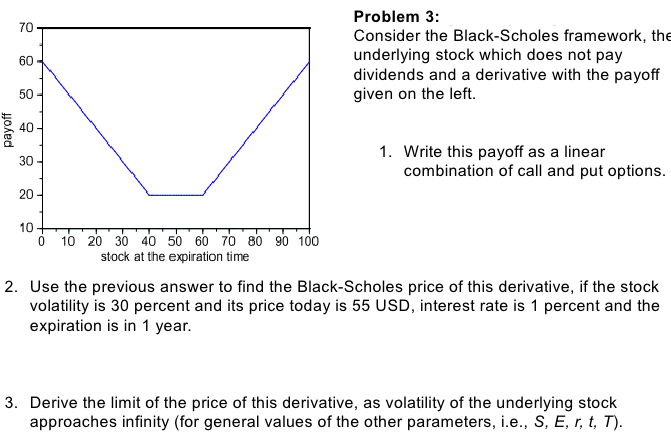
- From Yue-Kuen Kwok: Mathematical Models of Financial Derivatives

- From Yue-Kuen Kwok: Mathematical Models of Financial Derivatives

Further questions:- Plot the option price as a function of the stock volatility. Show that the option price is not necessarily an increasing function of the volatility (even though the payoff is an increasing function of the stock price at expiration).
- Using the previous graph, sketch the vega of the option. Ten compute it anlytically and plot its graph.
- Compute the delta of the option. Find its limit as the stock price approaches infinity and give financial interpretation of this result.
- Show that if the payoff of a derivative is never less than zero and is strictly positive on some interval, then the derivative price is strictly positive for any stock price at any time before expiration.
- Show that if V is a solution to the Black-Scholes PDE, then also
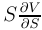 is a solution to the equation.
Use this property to show that if the payoff is an increasing differentiable function of the stock price at expiration, that the derivative price is an increasing function of the stock price at any time before
expiration.
is a solution to the equation.
Use this property to show that if the payoff is an increasing differentiable function of the stock price at expiration, that the derivative price is an increasing function of the stock price at any time before
expiration.
- Show that if the payoff is a convex twice differentiable function of the stock price at expiration, that the derivative price is a convex function of the stock price at any time before expiration. Hint: Firstly prove a similar lemma as in the previous example.
Financial derivatives - exercises
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://www.iam.fmph.uniba.sk/institute/stehlikova/
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://www.iam.fmph.uniba.sk/institute/stehlikova/