Numerické riešenie Black-Scholesovej PDR
:: Prečo numerické riešenie ::
- Načo riešiť rovnicu numericky, keď máme jej explicitné rieenie?
- Explicitné riešenie máme pre európsku call a put opciu. Pre iné deriváty takýto vzorec nemusí existovať. (To je prípad napríklad amerických call a put opcií, ktorými sa ešte budeme zaoberať. A mnohých ďalších.) Riešenie sa však dá nájsť numericky.
- To, že použitie numerických schém vyskúšame najskôr v prípade, v ktorom máme k dispozícii explicitné riešenie, má tú výhodu, že môžeme overiť presnosť získaných numerických výsledkov.
:: Transformácia Black-Scholesovej rovnice ::
- Black-Scholesova rovnica
- je to parabolická PDR, ktorá sa dá transformovať na rovnicu vedenia tepla so zadanou začiatočnou podmienkou.
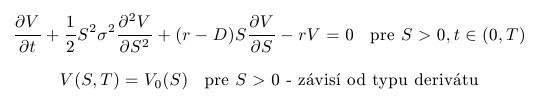
- Transformácia premenných
- Máme koncovú podmienku čase T (čas exspirácie opcie), nie začiatočnú. To vyriešime transformáciou
To znamená, že novou premennou, namiesto času t, bude čas zostávajúci do exspirácie.
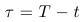
- Premenná S (cena akcie) je kladná. Premennú, ktorá nadobúda
všetky reálne hodnoty dostaneme zlogaritmovaním. Nová premenná teda bude
Hodnoty x blízke nule zodpovedajú cenám akcie, ktoré sú blízke exspiračnej cene opcie. Záporné hodnoty x predstavujú ceny akcie, ktoré sú nižšie ako je exspiračná cena. Analogicky, kladné hodnoty x predstavujú ceny akcie, ktoré sú vyššie ako je exspiračná cena. Na transformáciu rovnice by stačila logaritmická transformácia, ale - ako uvidíme neskôr - táto bude výhodnejšia z numerického hľadiska.
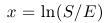
- Máme koncovú podmienku čase T (čas exspirácie opcie), nie začiatočnú. To vyriešime transformáciou
- Transformácia na RVT
- Rovnica, ktorú dostaneme týmito transformáciami, je parabolická
rovnica, ale už s konštantnými koeficientami. Túto rovnicu vieme
transformovať na rovnicu vedenia tepla transformáciou
kde konštanty určíme tak, aby po tranformácii vznikla práve RVT. Tá správna voľba konštánt je
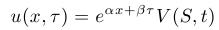 Vedie k rovnici
Vedie k rovnici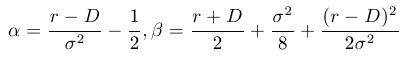
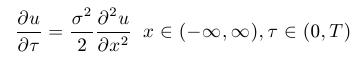
- Rovnica, ktorú dostaneme týmito transformáciami, je parabolická
rovnica, ale už s konštantnými koeficientami. Túto rovnicu vieme
transformovať na rovnicu vedenia tepla transformáciou
- Transformácia koncovej podmienky:
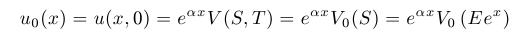
- Vyriešením tejto RVT a spätnou transformáciou dostaneme explicitné Black-Scholesove vzorce, ktoré sme používali v predchádzajúcich cvičeniach. Teraz však chceme túto rovnicu riešiť numericky.
:: Diskretizácia ::
- Premenná x je z neohraničeného intervalu, nadobúda hodnoty od mínus
nekonečna do plus nekonečna. Numericky budeme úlohu riešiť pre x z
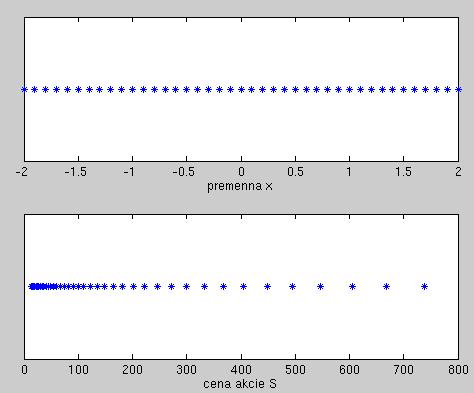
ohraničeného intervalu [-L, L], kde L bude dosť veľké číslo. Na obrázku
je delenie intervalu premennej x, a zodpovedajúce delenie pre cenu
akcie, ak je exspiračná cena 100 USD.
Všimnime si, že tento interval [-L, L] nemusíme meniť pre opciu s inou exspiračnou cenou. O vhodné body S sa postará transformácia x = ln(S/E), ktorú sme použili namiesto jednoduchej logaritmickej transformácie x = ln(S).
Kvôli tomu, že sme výpočet obmedzili na ohraničený interval, musíme k rovnici dodať okrajové podmienky v krajných bodoch. Krajné body zodpovedajú cenám akcie, ktoré sú veľmi malé, blízke nule (x=-L) a cenám, ktoré sú veľmi veľké a približujú sa k nekonečnu (x=L). Pre takéto limitné hodnoty použijeme aproximácie:
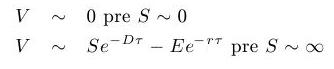
- Ďalej potrebujeme diskretrizovať RVT. Sú dve možnosti:
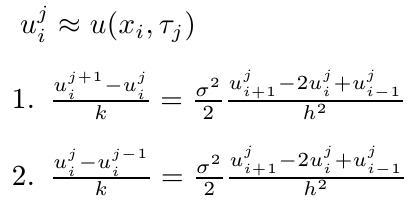
Prvý prístup (explicitná schéma) vyzerá byť jednoduchší. Máme začiatočnú podmienku. Z nej vypočítame hodnoty v nasledujúcej časovej vrstve. Tieto použijeme na výpočet riešenia v ďalšej časovej vrstve, atď. Na konvergenciu metódy je však potrebné splnenie podmienky na vzťah časového a priestorového kroku. Táto podmienka môže prakticky viesť k nevyhnutnosti zvoliť veľmi malý časový krok - kvôli konvergencii metódy, nie kvôli tomu, že by sme riešenie potrebovali v mnohých tak blízkych časových okamihoch.
V druhom prístupe (implicitná schéma) riešime na každej časovej vrstve sústavu lineárnych rovníc.
:: Implicitná schéma pre call opciu ::
-
Zvolíme parametre opcie:
E <- 50 r <- 0.04 D <- 0.12 sigma <- 0.4
- Zvolíme parameter L, určujúci oblasť, na ktorej budeme riešenie počítať:
L <- 2
a parametre delenia:n <- 20 h <- L/n T <- 1 m <- 12 k <- T/m
- Definujeme konštanty potrebné na transformáciu rovnice:
alpha <- (r-D)/(sigma^2) - 0.5 beta <- (r+D)/2 + (sigma^2)/8 + ((r-D)^2)/(2*sigma^2)
- Pre riešenie trasformovanej rovnice definujeme okrajové
podmienky:
phi <- function(tau) 0 psi <- function(tau) E*exp(alpha*L + beta*tau)*(exp(L - D*tau) - exp(-r*tau))
a začiatočnú podmienku:u0 <- function(x) E*exp(alpha*x)*pmax(0, exp(x)-1)
- Vytvoríme maticu, do ktorej budeme vkladať riešenie:
sol <- matrix(0, nrow=2*n + 1, ncol=m+1)
a body delenia v čase a v priestore:x <- seq(from=-L, by=h, to=L) tau <- seq(from=0, by=k, to=T)
Úloha pre vás: Vložte do matice okrajové podmienky a začiatocnú podmienku.
- Na výpočet každej časovej vrstvy budeme potrebovať vyriešiť
sústavu lineárnych rovníc. Definujeme teraz premenné, ktoré obsahujú
hodnoty vystupujúce v trojdiagonálnej matici tejto sústavy:
a <- -0.5*(sigma^2)*k/(h^2) b <- 1 - 2*a
Pri výpočte prvej časovej vrstvy (teda hodnoty v čase k) máme nasledovnú pravú stranu:rhs <- sol[c(2:(2*n)),1] rhs[1] <- rhs[1] - a*phi(k) rhs[2*n-1] <- rhs[2*n-1] - a*psi(k)
Na riešenie systému rovníc použijeme najskôr Gauss-Seidelovu metódu:Môžete použiť funkciu:
gs <- function(a,b,rhs,v0,eps,N) { n.system <- length(v0) v <- v0 for (iter in 1:N) { v[1] <- (rhs[1] - a*v[2])/b for (i in 2:(n.system-1)) v[i] <- (rhs[i] - a*(v[i-1] + v[i+1]))/b v[n.system] <- (rhs[n.system] - a*v[n.system - 1])/b } gs <- v }
Úlohy pre vás:- Vypočítajte riešenie na prvej časovej vrstve a vložte ho do matice s riešením (ako začiatočnú aproximáciu riešenia môžete použiť hodnoty z predchádzajúcej časovej vrstvy, zvoľte si kritérium na zastavenie iterácií).
- Transformujte získané riešenie na riešenie Black-Scholesovej rovnice.
- Naprogramujte cyklus, v ktorom sa vypočíta riešenie na každej časovej vrstve.
- Porovnajte s presnými hodnotami z Black-Scholesovho vzorca.
Ukážka výstupu: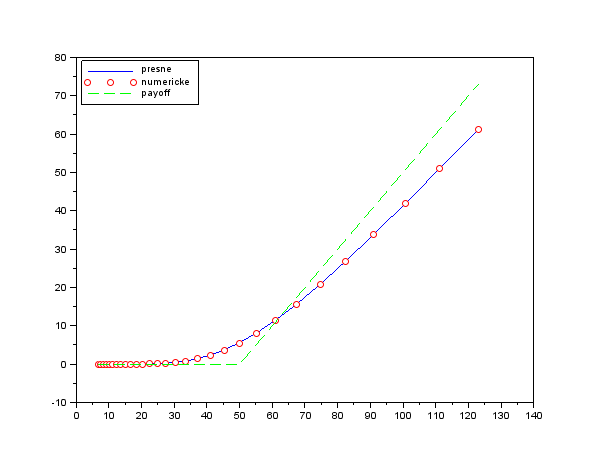
:: SOR metóda ::
- Úpravou funkcie gs vytvorte funkciu sor, ktorá bude mať navyše parameter omega. Následne ju použite na výpočet ceny opcie. Jedinou zmenou v hlavnom kóde bude volanie funkcie sor namiesto funkcie gs.
- Návod pre prvú zložku, analogicky pre ostatné:
vOld <- v[1] vGS <- (rhs[1] - a*v[2])/b; v[1] <- omega*vGS + (1-omega)*vOld
- Voľba parametra omega v SOR metóde:
- Pre túto úlohu SOR konverguje pri ľubovoľnej omege z intervalu (0, 2).
- Aby sme dosiahli čo najrýchlejšiu konvergenciu, iteračná matica by mala mať čo najmenší spektrálny polomer.
- Závislosť spektrálneho polomeru od parametrov úlohy a delenia si môžete vyskúšať tu: [ui.R], [server.R]
- Návod k odvodeniu spektrálneho polomeru iteračnej matice (použité v predchádzajúcom kóde, odvodenie je medzi zadaniami na poslednej strane slajdov o SOR metóde): http://www.cs.rpi.edu/~flaherje/ -> Partial Differential Equations -> Solution Techniques for Elliptic Problems
:: Ďalšie príklady na precvičenie ::
- Explicitná schéma. Naprogramujte explicitnú schému na
oceňovanie opcií. Spomínaná podmienka (na zaručenie konvergencie) pre
vzťah medzi priestorovým a časovým krokom je
Nazýva sa CLF (Courant-Friedrichs-Lewy) podmienka. Ukážte príklad výpočtu, kedy táto podmienka je splnená a príklad výpočtu, keď splnená nie je.
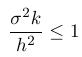
Ukážka výstupu: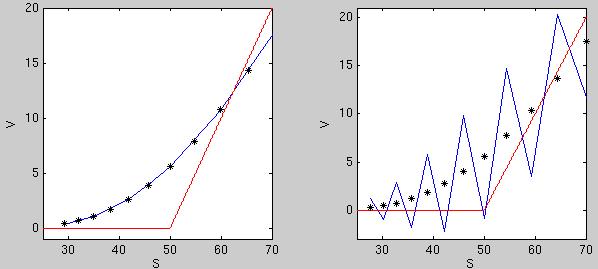
- Binomický strom. Ak v explicitnej schéme zvolíme
dostaneme nasledovný predpis:
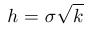 To znamená, že na výpočet určitej hodnoty potrebujeme hodnoty z predchádzajúcej časovej vrstvy v susedných bodoch priestorového delenia. Preto sa tento špeciálny prípad nazýva metódou binomického stromu.
To znamená, že na výpočet určitej hodnoty potrebujeme hodnoty z predchádzajúcej časovej vrstvy v susedných bodoch priestorového delenia. Preto sa tento špeciálny prípad nazýva metódou binomického stromu.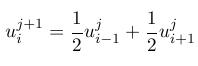 Naprogramujte túto metódu.
Naprogramujte túto metódu.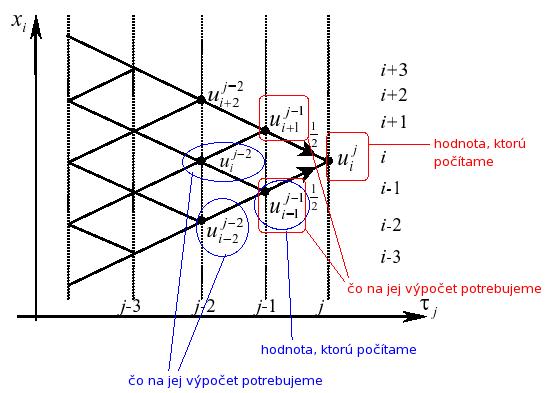
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/