Naivný Bayesov klasifikátor

Metódy riešenia úloh z pravdepodobnosti a štatistiky

Klasifikátor

  • Máme dáta, chceme ich vedieť zatriediť do skupín.
  • Časť dát na natrénovanie klasifikátora (napríklad odhadnutie parametrov), potom ho môžeme otestovať a používať
  • Napríklad: Je tento mail spam alebo nie?

Bayesov klasifikátor

Postup:

  • Triedy \(C_1, C_2, \dots, C_k\)
  • Na dátach si všímame určité veličiny \(X_1, \dots X_m\)
  • Pre pozorovanie s hodnotami \(x_1, \dots x_n\) vypočítame pravdepodobnosti \[\mathbb{P}({\textrm{pozorovanie je z } C_k} | X_1 = x_1 \cap \dots\cap X_m = x_m)\]
  • Zaradíme ho do tej triedy, pre ktorú je táto pravdepodobnosť najvyššia

Všimnime si:

  • Pravdepodobnosti sú \[ \frac{\mathbb{P}({\textrm{pozorovanie je z} C_k} \cap X_1 = x_1 \cap \dots \cap X_m = x_m)}{\mathbb{P}(X_1 = x_1 \cap \dots \cap X_m = x_m)}\]

  • Menovatele sú rovnaké \(\rightarrow\) na nájdenie maximálnej hodnoty stačí porovnávať čitatele

  • Ak chceme pravdepodobnosti, vektor čitateľov stačí prenásobiť konštantou tak, aby bol súčet zložiek rovný 1.

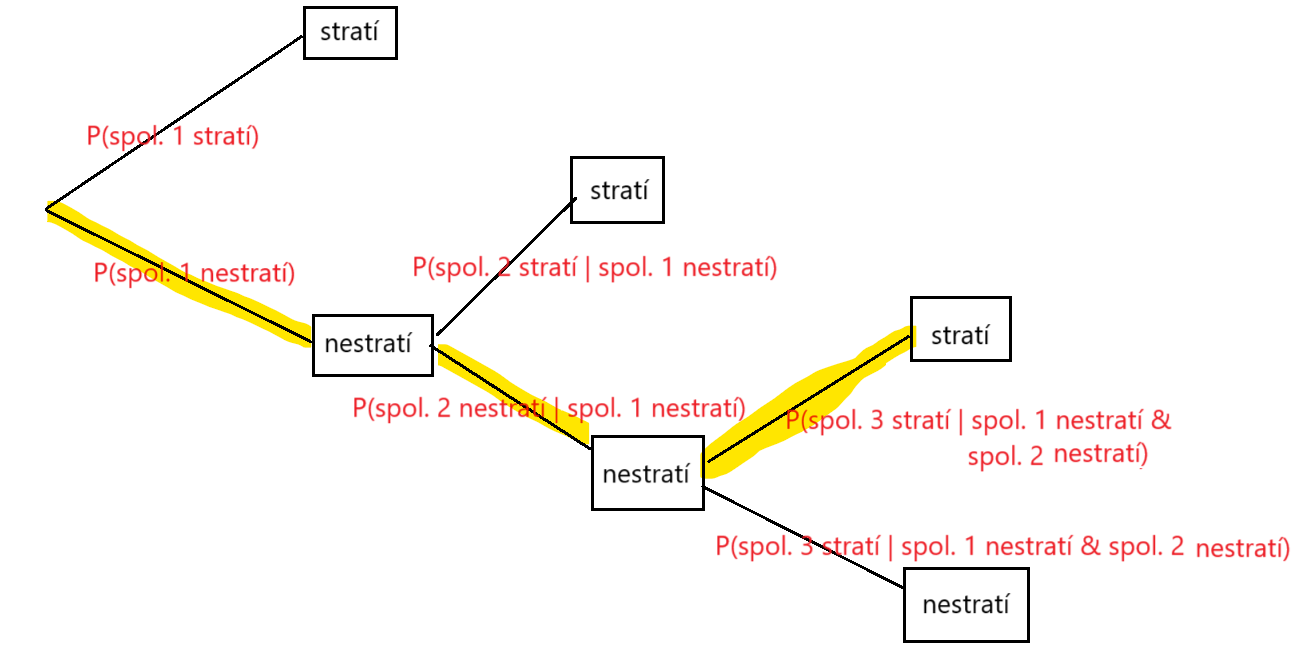
Strom z príkladu o preprave batožiny

Násobenie pravdepodobností a Bayesov klasifikátor

\(\mathbb{P}(\textrm{spol. 1 nestratí & spol. 2 nestratí & spol. 3 stratí})\) je súčin pravdepodobností:

  • \(\mathbb{P}(\textrm{spol. 1 nestratí})\)
  • \(\mathbb{P}(\textrm{spol. 2 nestratí | spol. 1 nestratí})\)
  • \(\mathbb{P}(\textrm{spol. 3 stratí | spol. 1 nestratí & spol. 2 nestratí})\)

Vo všeobecnosti pre klasifikátor potrebujeme súčin pravdepodobností:

  • \(\mathbb{P}(\textrm{pozorovanie je z } C_k)\)
  • \(\mathbb{P}(X_1 = x_1 \textrm{ | pozorovanie je z } C_k)\)
  • \(\mathbb{P}(X_2 = x_2 | X_1 = x_1 \cap \textrm{ pozorovanie je z } C_k)\)
  • \(\mathbb{P}(X_3 = x_3 | X_1 = x_1 \cap X_2 = x_2 \cap \textrm{ pozorovanie je z } C_k)\)
  • atď.

Naivný klasifikátor predpokladá:

  • \(\mathbb{P}(X_2 = x_2 | X_1 = x_1 \cap \textrm{ pozorovanie je z } C_k)\) je rovnaká ako \(\mathbb{P}(X_2 = x_2 | \textrm{ pozorovanie je z } C_k)\)

  • \(\mathbb{P}(X_3 = x_3 | X_1 = x_1 \cap X_2 = x_2 \cap \textrm{ pozorovanie je z } C_k)\) je rovnaká ako \(\mathbb{P}(X_3 = x_3 | \textrm{ pozorovanie je z } C_k)\)

  • atď.

Príklad

  • Hlasovania, chceme rozlíšiť republikánov a demokratov.
data(HouseVotes84, package = "mlbench")
head(HouseVotes84)
       Class   V1 V2 V3   V4   V5 V6 V7 V8 V9 V10  V11  V12 V13 V14 V15  V16
1 republican    n  y  n    y    y  y  n  n  n   y     y   y   y   n    y
2 republican    n  y  n    y    y  y  n  n  n   n    n    y   y   y   n 
3   democrat   y  y     y  y  n  n  n   n    y    n   y   y   n    n
4   democrat    n  y  y    n   y  n  n  n   n    y    n   y   n   n    y
5   democrat    y  y  y    n    y  y  n  n  n   n    y    y   y   y    y
6   democrat    n  y  y    n    y  y  n  n  n   n    n    n   y   y   y    y

Koľko je v jednotlivých stĺpcoch NA hodnôt:

apply(HouseVotes84,
      2, # po stlpcoch
      FUN = function(x) sum(is.na(x)))
Class    V1    V2    V3    V4    V5    V6    V7    V8    V9   V10   V11   V12 
    0    12    48    11    11    15    11    14    15    22     7    21    31 
  V13   V14   V15   V16 
   25    17    28   104

Vynecháme z analýzy posledné hlasovanie a zoberieme úplné riadky - to budú naše dáta (chýbajúce hodnoty teraz nebudeme riešiť):

indexy_uplne <- complete.cases(HouseVotes84[, -17])
votes <- HouseVotes84[indexy_uplne, -17]
head(votes)
        Class V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 V15
2  republican  n  y  n  y  y  y  n  n  n   n   n   y   y   y   n
6    democrat  n  y  y  n  y  y  n  n  n   n   n   n   y   y   y
9  republican  n  y  n  y  y  y  n  n  n   n   n   y   y   y   n
20   democrat  y  y  y  n  n  n  y  y  y   n   y   n   n   n   y
24   democrat  y  y  y  n  n  n  y  y  y   n   n   n   n   n   y
25   democrat  y  n  y  n  n  n  y  y  y   n   n   n   n   n   y

Rozdelíme dáta na trénovaciu a testovaciu časť.

Poznámka: Prečo nie je cieľom len presne nafitovať dáta a potom to použiť na predikcie:

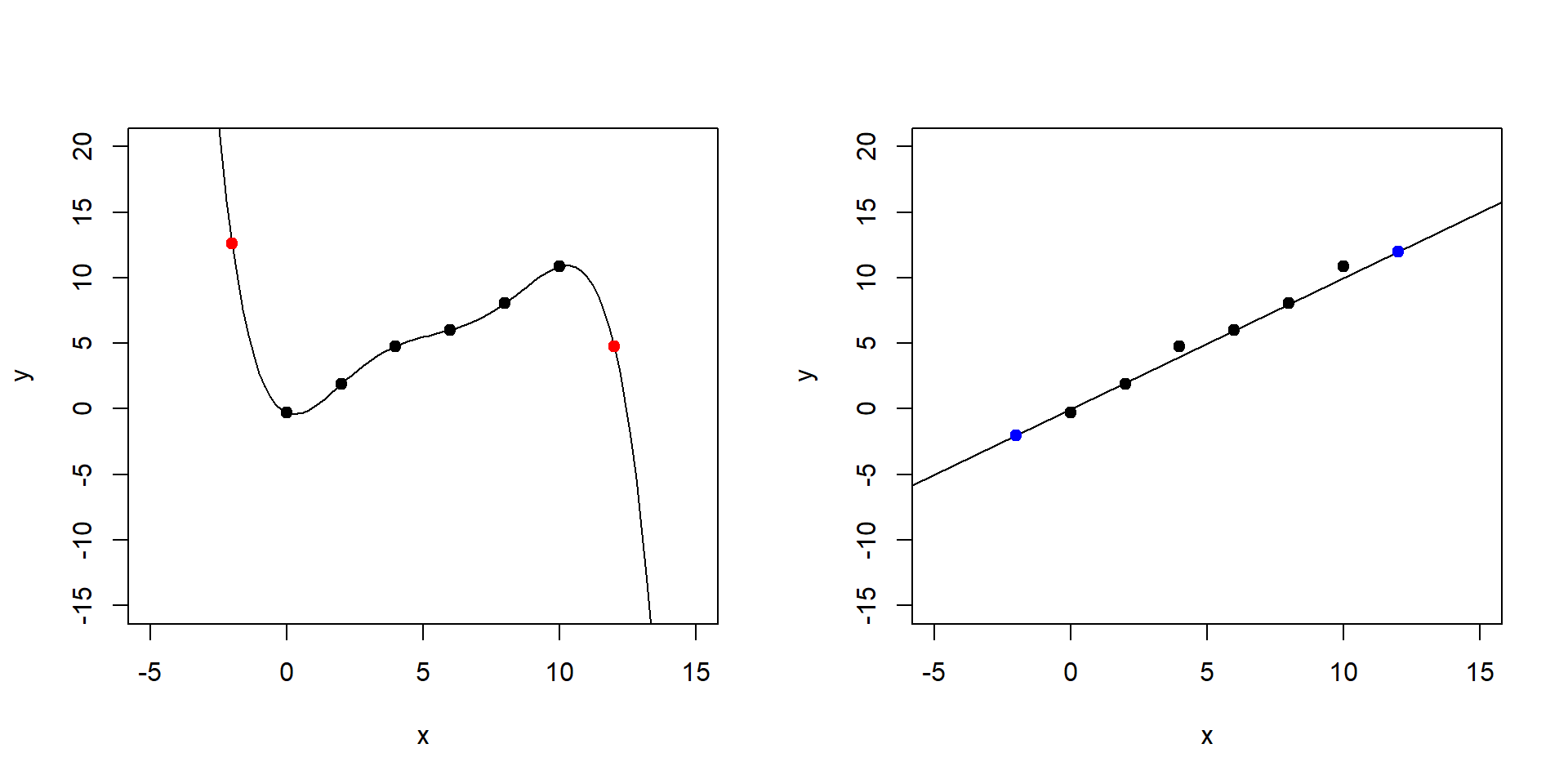
library(caret)
set.seed(123)
train_index <- createDataPartition(votes$Class, 
                                   p = 0.8,   # podiel dat v trenovacej casti
                                   list = FALSE)
votes_train <- votes[train_index, ]
votes_test <- votes[-train_index, ]  

nrow(votes_train)
[1] 225
nrow(votes_test)
[1] 56
head(votes_train)
        Class V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 V15
2  republican  n  y  n  y  y  y  n  n  n   n   n   y   y   y   n
6    democrat  n  y  y  n  y  y  n  n  n   n   n   n   y   y   y
25   democrat  y  n  y  n  n  n  y  y  y   n   n   n   n   n   y
26   democrat  y  n  y  n  n  n  y  y  y   y   n   n   n   n   y
27   democrat  y  n  y  n  n  n  y  y  y   n   y   n   n   n   y
28   democrat  y  y  y  n  n  n  y  y  y   n   y   n   n   n   y

  • Spravme na základe dát votes_train naivný Bayesovský model, ktorý bude využívať výsledky hlasovaní 1, 8, 15.
  • Potom pomocou neho predikujme napr.
votes_test[1, c("V1", "V8", "V15")]
  V1 V8 V15
9  n  n   n
  • Potrebujeme:
table(votes_train$Class)

  democrat republican 
       132         93 
table(votes_train$Class, votes_train$V1)
            
              n  y
  democrat   54 78
  republican 72 21
table(votes_train$Class, votes_train$V8)
            
               n   y
  democrat    25 107
  republican  80  13
table(votes_train$Class, votes_train$V15)
            
              n  y
  democrat   48 84
  republican 81 12

Postup v R-ku:

library(e1071)
bayes <- naiveBayes(Class ~ V1 + V8 + V15, data = votes_train)      
bayes

Naive Bayes Classifier for Discrete Predictors

Call:
naiveBayes.default(x = X, y = Y, laplace = laplace)

A-priori probabilities:
Y
  democrat republican 
 0.5866667  0.4133333 

Conditional probabilities:
            V1
Y                    n         y
  democrat   0.4090909 0.5909091
  republican 0.7741935 0.2258065

            V8
Y                    n         y
  democrat   0.1893939 0.8106061
  republican 0.8602151 0.1397849

            V15
Y                    n         y
  democrat   0.3636364 0.6363636
  republican 0.8709677 0.1290323
predikcie_raw <- predict(bayes, newdata = votes_test, type = "raw")
head(predikcie_raw)
       democrat  republican
[1,] 0.06449578 0.935504221
[2,] 0.99067392 0.009326075
[3,] 0.99067392 0.009326075
[4,] 0.06449578 0.935504221
[5,] 0.99067392 0.009326075
[6,] 0.99067392 0.009326075
predikcie <- predict(bayes, newdata = votes_test)
head(predikcie)
[1] republican democrat   democrat   republican democrat   democrat  
Levels: democrat republican
table(predikcie, votes_test$Class)
            
predikcie    democrat republican
  democrat         29          4
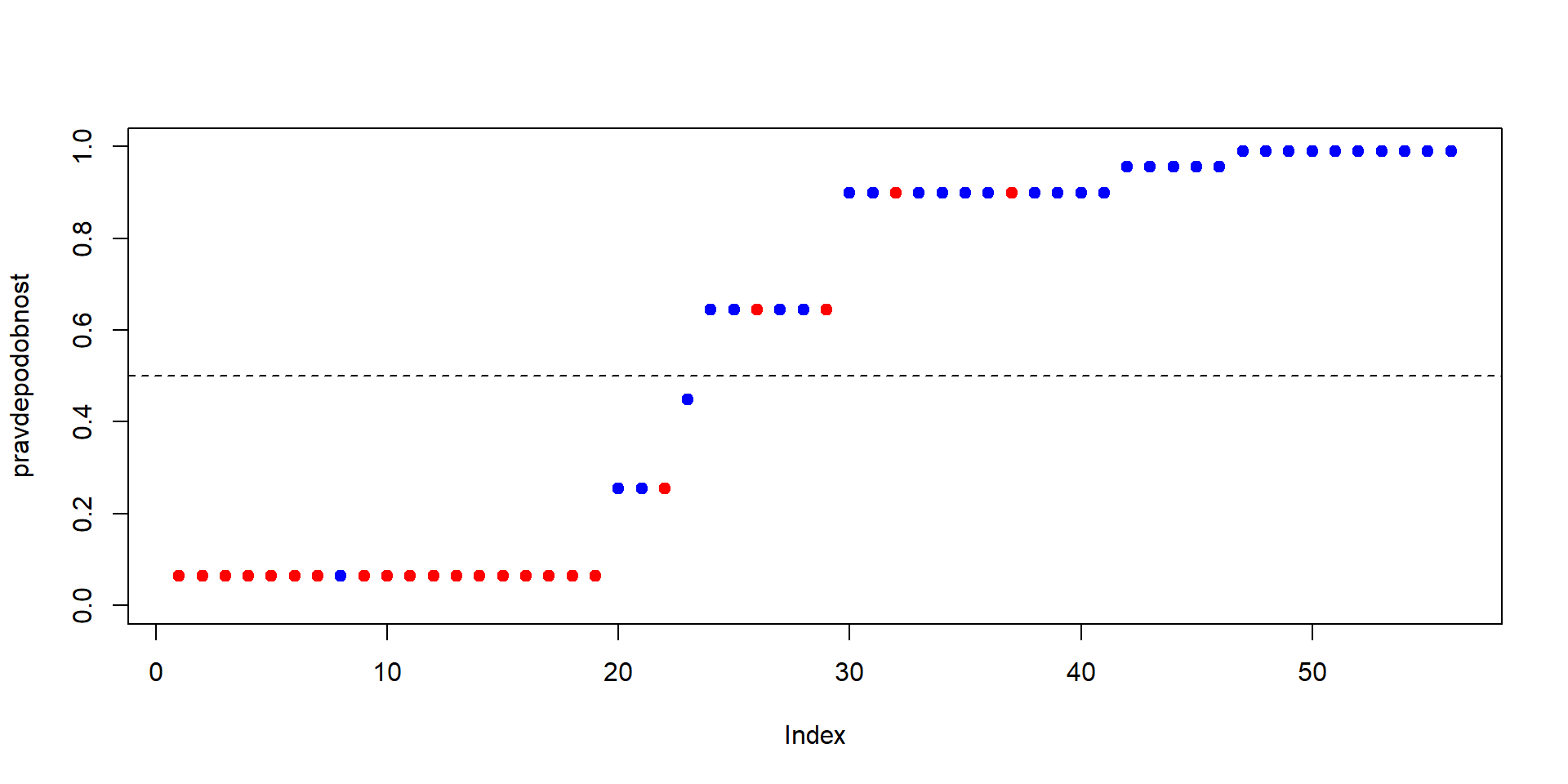
  republican        4         19

Jedna možná vizualizácia:

head(predikcie_raw)
       democrat  republican
[1,] 0.06449578 0.935504221
[2,] 0.99067392 0.009326075
[3,] 0.99067392 0.009326075
[4,] 0.06449578 0.935504221
[5,] 0.99067392 0.009326075
[6,] 0.99067392 0.009326075
unique(sort(predikcie_raw[, 1]))
[1] 0.06449578 0.25452597 0.44884769 0.64486532 0.89992692 0.95545564 0.99067392
table(round(predikcie_raw[,1], 5))

 0.0645 0.25453 0.44885 0.64487 0.89993 0.95546 0.99067 
     19       3       1       6      12       5      10

Zobrazíme odhadnuté pravdepodobnosti a farebne odlíšime republikánov a demokratov.