Kombinatorická pravdepodobnosť (1)

Metódy riešenia úloh z pravdepodobnosti a štatistiky

Príklad 1: Vystupovanie z výťahu (stredná hodnota)

Do výťahu nastúpilo na prízemí osemposchodovej budovy 10 ľudí. Každý vystupuje s rovnakou pravdepodobnosťou na každom z poschodí, nezávisle od ostatných. Aká je stredná hodnota počtu poschodí, na ktorých výťah zastane, lebo na tomto poschodí niekto vystupuje?

Simulačné riešenie

Generovanie vystupovania z výťahu:

pocet_poschodi <- 8
pocet_ludi <- 10

set.seed(123) # kvoli reprodukovatelnosti

kde_vystupuju <- sample(1:pocet_poschodi, size = pocet_ludi, replace = TRUE)
kde_vystupuju

 [1] 7 7 3 6 3 2 2 6 3 5

kde_zastane <- unique(kde_vystupuju)
kde_zastane

[1] 7 3 6 2 5

pocet_zastaveni <- length(kde_zastane)
pocet_zastaveni

[1] 5

Princíp simulácií: Zopakujeme takéto generovanie veľa krát a z výsledkov spravíme štatistiku.

pocet_poschodi <- 8
pocet_ludi <- 10

vystupovanie <- function(pocet_poschodi, pocet_ludi){
  kde_vystupuju <- sample(1:pocet_poschodi, size = pocet_ludi, replace = TRUE)
  kde_zastane <- unique(kde_vystupuju)
  pocet_zastaveni <- length(kde_zastane)
  return(pocet_zastaveni)
}

set.seed(123)
simulacie <- replicate(10^5, vystupovanie(8, 10))
mean(simulacie)

[1] 5.89972

Analytický výpočet

Spravíme na cvičení pri tabuli, základná myšlienka:

• Definujeme náhodné premennné \(X_i\),ktorá sa rovná 1, ak na \(i\)-tom poschodí niekto vystúpil, inak sa rovná nule.
• Potom definujeme \(X = X_1 + X_2 + \dots X_n\), kde \(n\) je počet poschodí - táto náhodná premenná vyjadruje počet poschodí, na ktorých niekto vystúpi
• Zaujíma nás jej stredná hodnota

Porovnanie simulácií s presným riešením

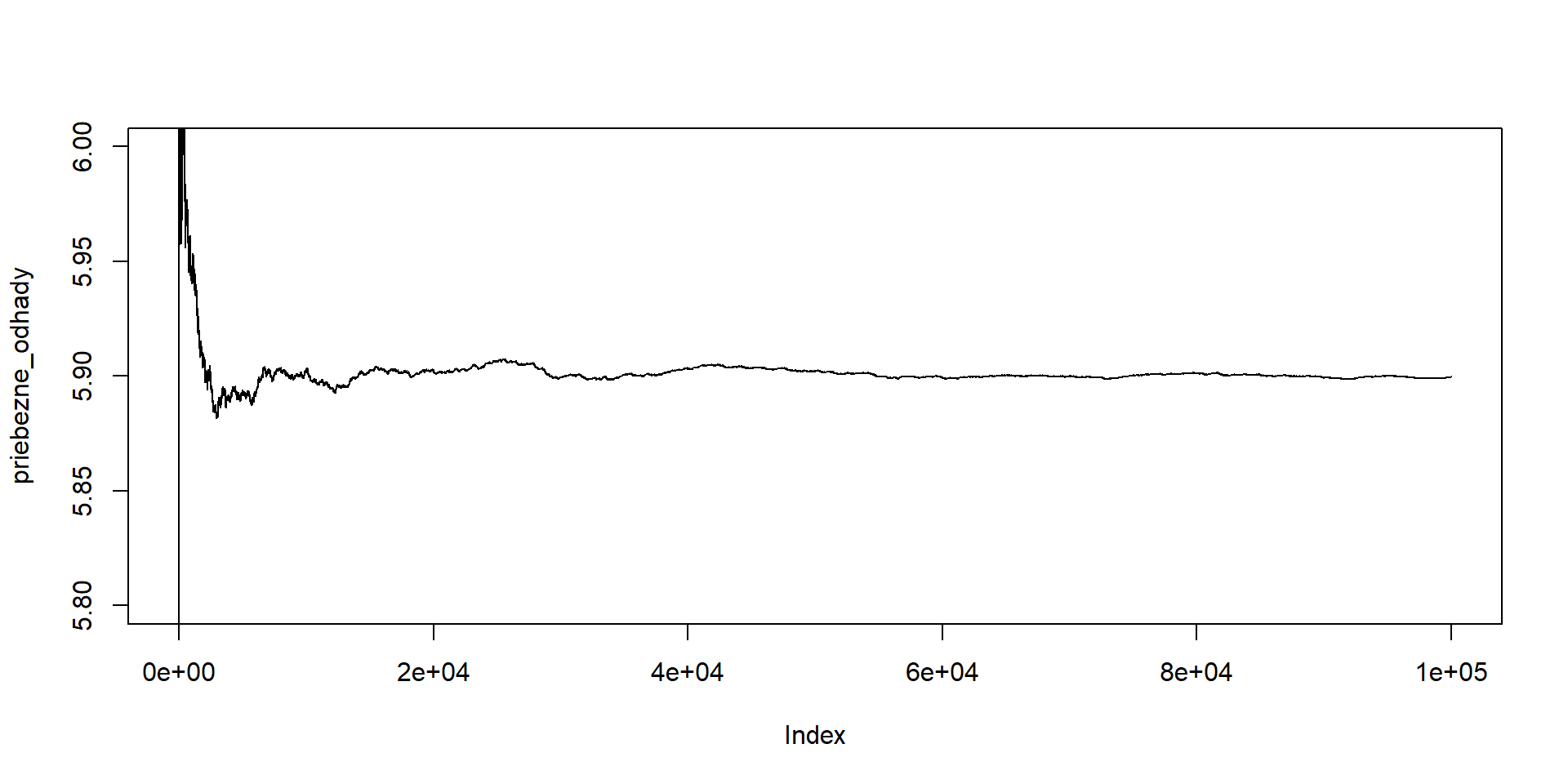
Očakávame, že priemer zo simulácií sa bude približovať k presnej strednej hodnote.

Zobrazíme priebežné priemery (po 1, 2, 3,… simuláciách):

priebezne_odhady <- cumsum(simulacie)/1:length(simulacie)
head(priebezne_odhady) # zaciatocne hodnoty vektora

[1] 5.000000 6.000000 6.333333 6.250000 6.200000 6.500000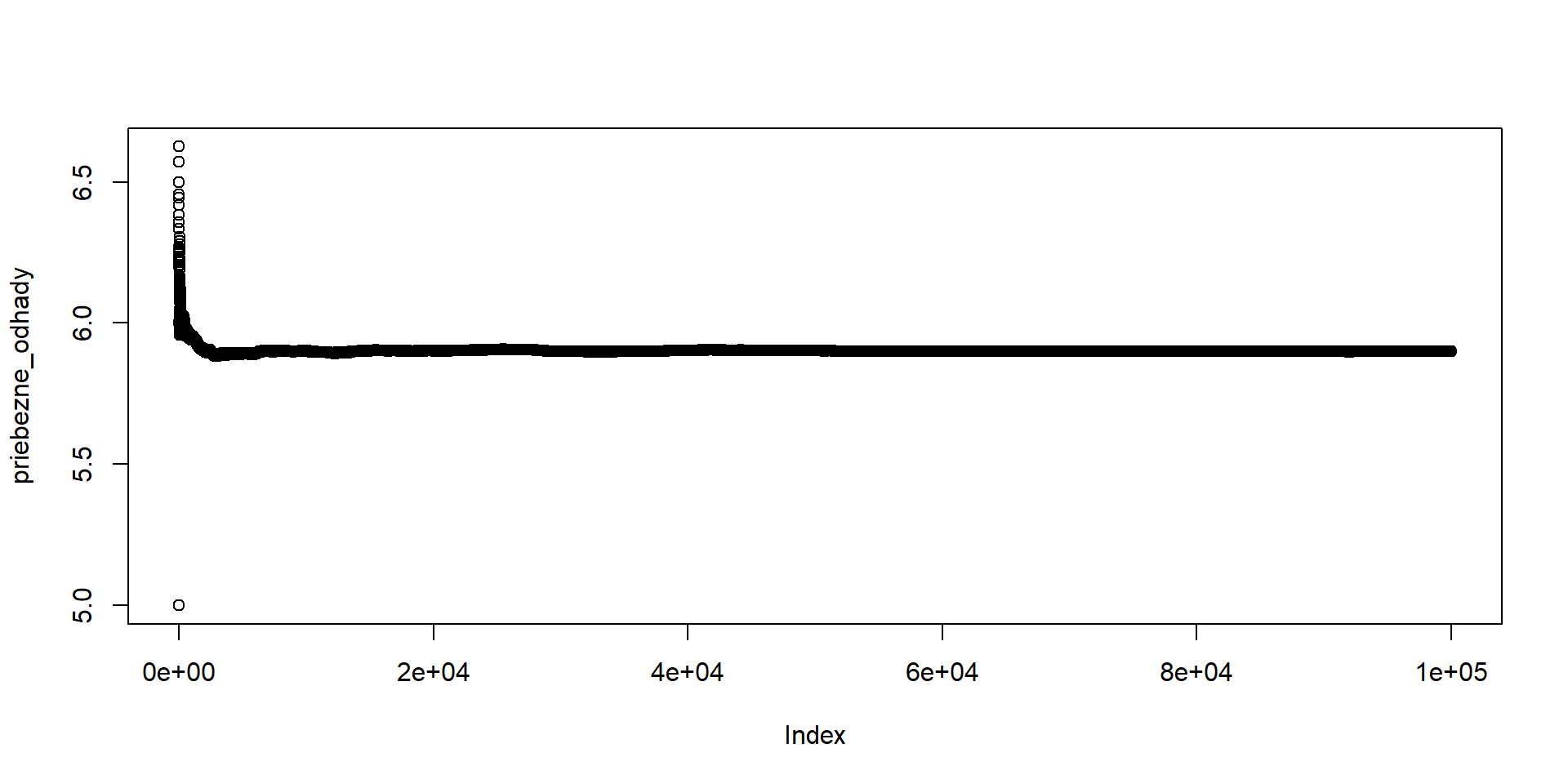

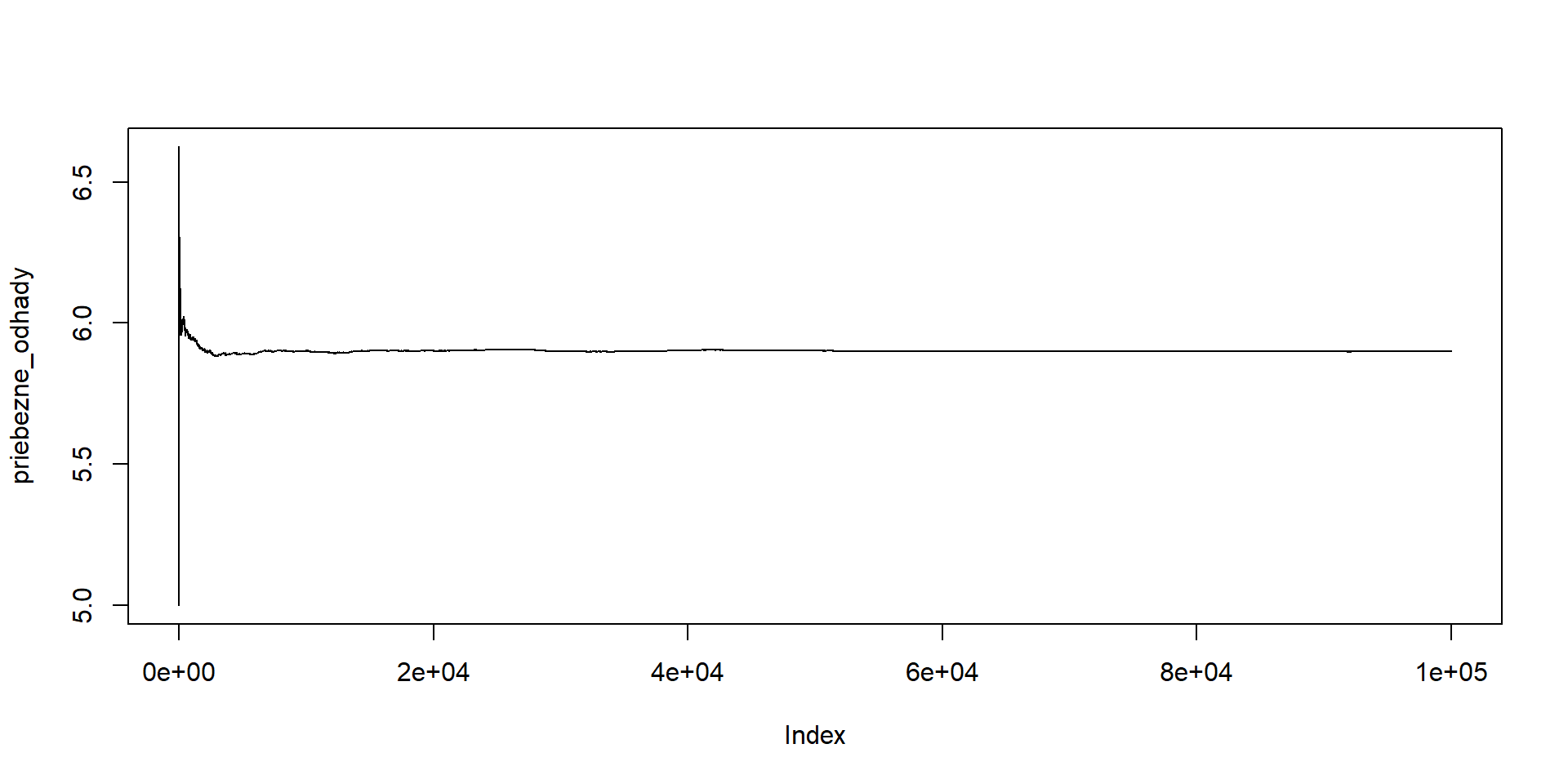
plot(priebezne_odhady)

# type = "l" -> ciara (line)
plot(priebezne_odhady, type = "l")

# ylim -> nastavenie rozsahu y-ovej osi
plot(priebezne_odhady, type = "l", ylim = c(5.8, 6))

Cvičenie na doma:

• Skopírujte si doterajšie výpočty a dokreslite do grafu presnú hodnotu pravdepodobnosti:

# abline dokresli do grafu priamku
# `h` dokresli horizontalnu priamku, DOPLNTE: treba zadat y-ovu suradnicu
# `lty` znamena line type, 2 je prerusovana ciara

abline(h = , lty = 2, color = "red")

Práca s vektormi v R

Ukážky vektorových výpočtov

x <- 1:5                # toto sme uz pouzivali
y <- c(4, 5, 10, -2, 5) # vytvorenie vektora pomocou `c

x + y

[1]  5  7 13  2 10

2*x

[1]  2  4  6  8 10

y^2

[1]  16  25 100   4  25

x == y

[1] FALSE FALSE FALSE FALSE  TRUE

Prehľadnosť kódu pri použití funkcií namiesto cyklov a if/else

Príklad A: súčet absolútnych hodnôt prehľadne

sum(abs(y))

[1] 26

Príklad B: súčet absolútnych hodnôt neprehľadne

sucet <- 0
for(i in 1:length(y)){
  if(y[i] >=0){
    absolutna_hodnota <- y[i]
  } else {
    absolutna_hodnota <- -y[i]
  }
  sucet <- sucet + absolutna_hodnota
}
sucet

[1] 26

Niekedy je rozdiel aj v rýchlosti

Budeme používať funkciu microbenchmark z balíka microbenchmark.

Nainštalovanie balíka:

install.packages("microbenchmark")

Načítanie balíka:

library("microbenchmark")

Použitie:

set.seed(123)
z <- sample(-10:10, size = 1000, replace = TRUE)

porovnanie <- microbenchmark(pristupA(z), pristupB(z))
porovnanie 

Unit: microseconds
        expr  min   lq    mean median    uq    max neval
 pristupA(z)  1.1  1.3  10.384    1.4  1.60  764.4   100
 pristupB(z) 63.3 64.4 104.114   64.8 65.65 3919.8   100

plot(porovnanie)

plot(porovnanie, ylim= c(0,100000))

Príklad 2: Vystupovanie z výťahu (závislosť od počtu ľudí)

Máme k dispozícii funkciu:

vystupovanie

function(pocet_poschodi, pocet_ludi){
  kde_vystupuju <- sample(1:pocet_poschodi, size = pocet_ludi, replace = TRUE)
  kde_zastane <- unique(kde_vystupuju)
  pocet_zastaveni <- length(kde_zastane)
  return(pocet_zastaveni)
}

Cvičenie: Napíšte funkciu odhad_strednej_hodnoty, ktorá na základe \(10^5\) simulácií odhadne strednú hodnotu počtu poschodí, na ktorých niekto vystúpi v osemposchodovej budove, ak zadáme počet ľudí nastupujúcich do výťahu.

odhad_strednej_hodnoty <- function(pocet_ludi){
  # niekde tu sa bude volat funkcia `vystupovanie` a `replicate`
}

# test
odhad_strednej_hodnoty(10)

Poznámka o vektorovom argumente v R

Niektoré funkcie vedia pracovať s vektorovým vstupom:

x <- seq(from = -3*pi, to = 3*pi, by = 0.001) # dalsi sposob vytvorenia vektora

y <- 2*sin(2*x) + 3*cos(5*x)
plot(x, y, type = "l")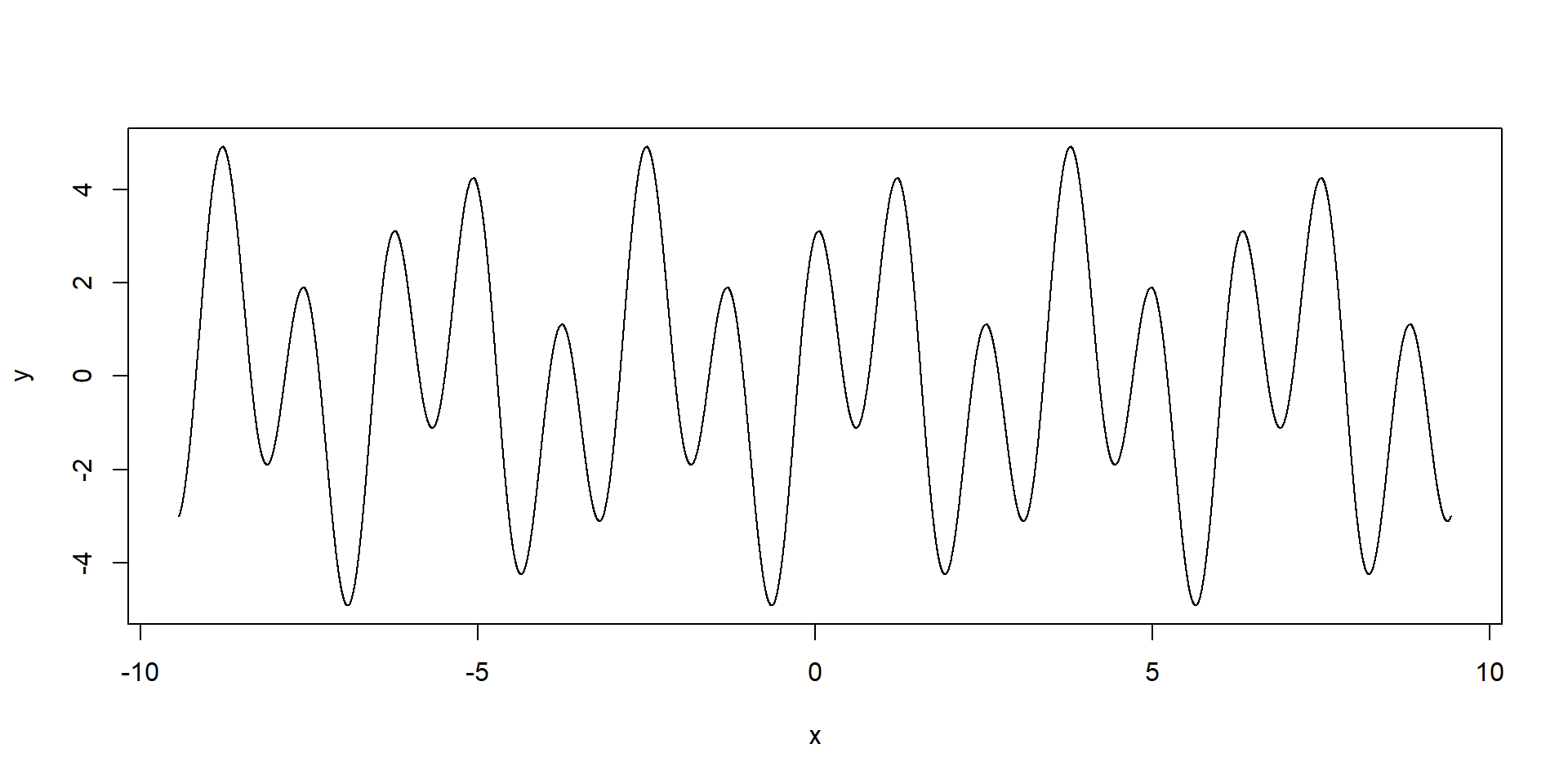

f <- function(t, a, b) a*sin(2*t) + b*cos(5*t)
# ak je vam to prehladnejsie, mozete pisat aj
# plot(t, f(x, a = -2, b = 3), type = "l")
plot(x, f(x, -2, 3), type = "l")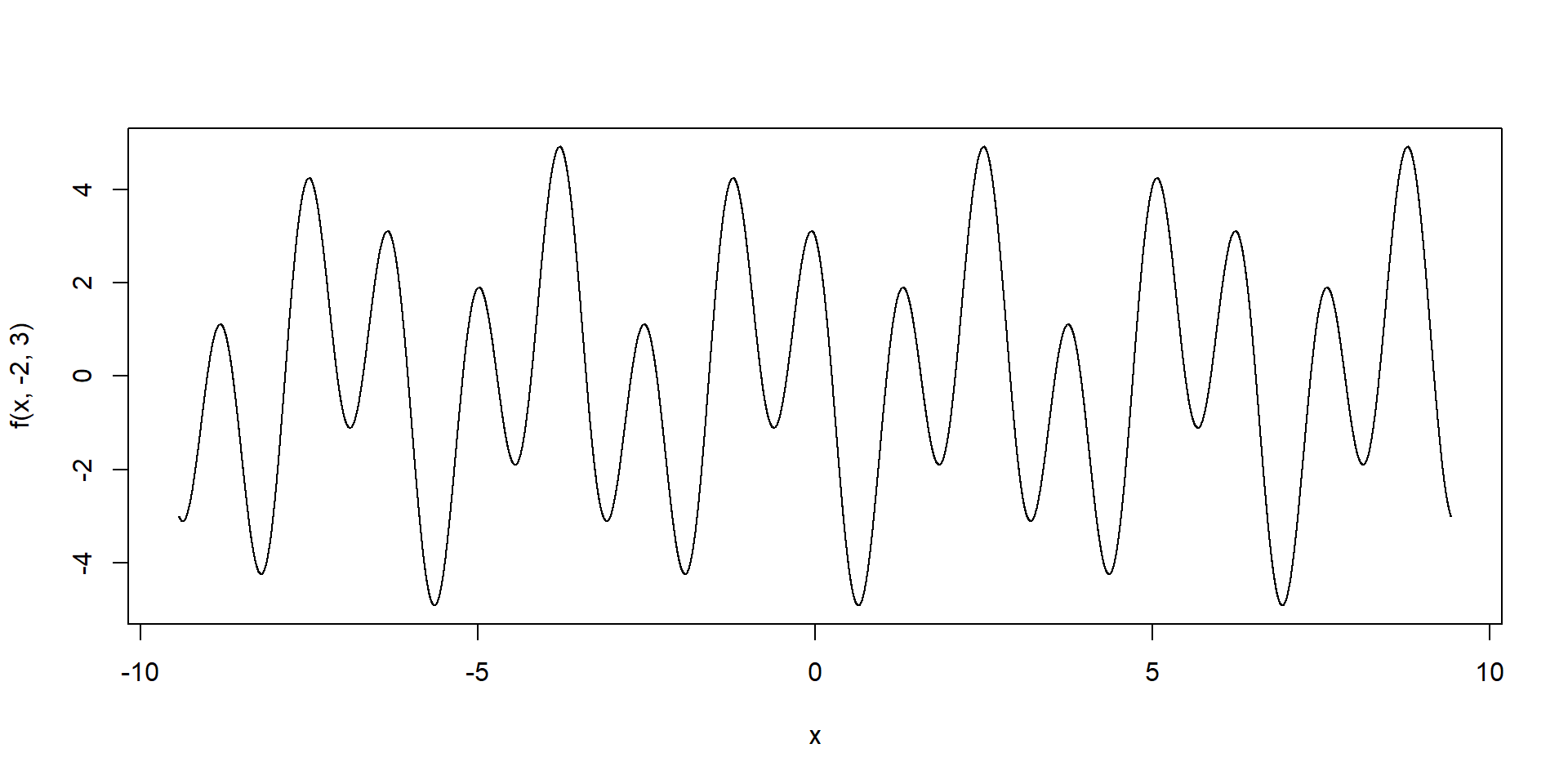

Ale napríklad:

Funkcia sapply

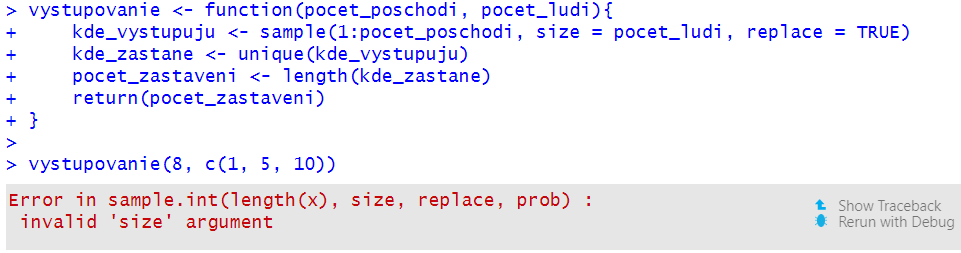
• apply = použitie nejakej funkcie pre zadané vstupy
• s = simplify, výstup sa zjednoduší, v tomto príklade na vektor

set.seed(123)
pocet <- 2:15
odhad <- sapply(pocet, odhad_strednej_hodnoty)
plot(pocet, odhad)

plot(pocet,  odhad, pch = 19)

Príklad 3: Vystupovanie z výťahu (pravdepodobnostné rozdelenie)

Ak 10 ľudí vystupuje na poschodiach osemposchodového domu, počet poschodí, na ktorých niekto vystúpil, nadobúda celočíselné hodnoty medzi 1 a 8. Chceme odhadnúť pravdepodobnosti jednotlivých možností.

Pripomeňme si simulácie:

head(simulacie)

[1] 5 7 7 6 6 8

Funkcia table vytvorí tabuľku s početnosťami:

tabulka <- table(simulacie)
tabulka

simulacie
    2     3     4     5     6     7     8 
    5   276  5291 26566 42759 22238  2865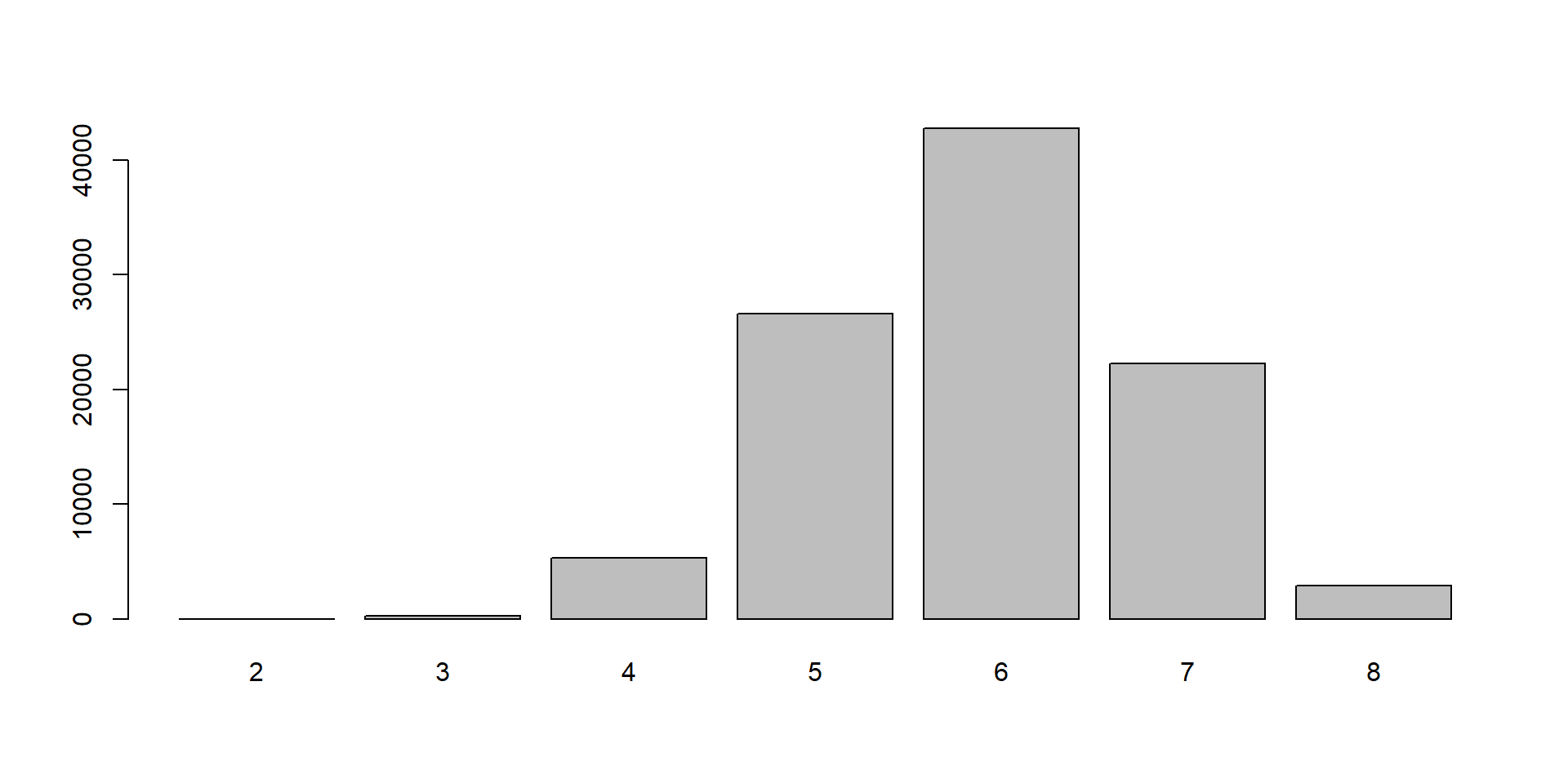 

barplot(tabulka)

Hodnota 1 sa nerealizovala (má príliš malú pravdepodobnosť), ale chceli by sme ju mať zaradenú do tabuľky s informáciou o nulovom počte výskytov.

simulacie <- factor(simulacie, levels = 1:8)
tabulka <- table(simulacie)
tabulka

simulacie
    1     2     3     4     5     6     7     8 
    0     5   276  5291 26566 42759 22238  2865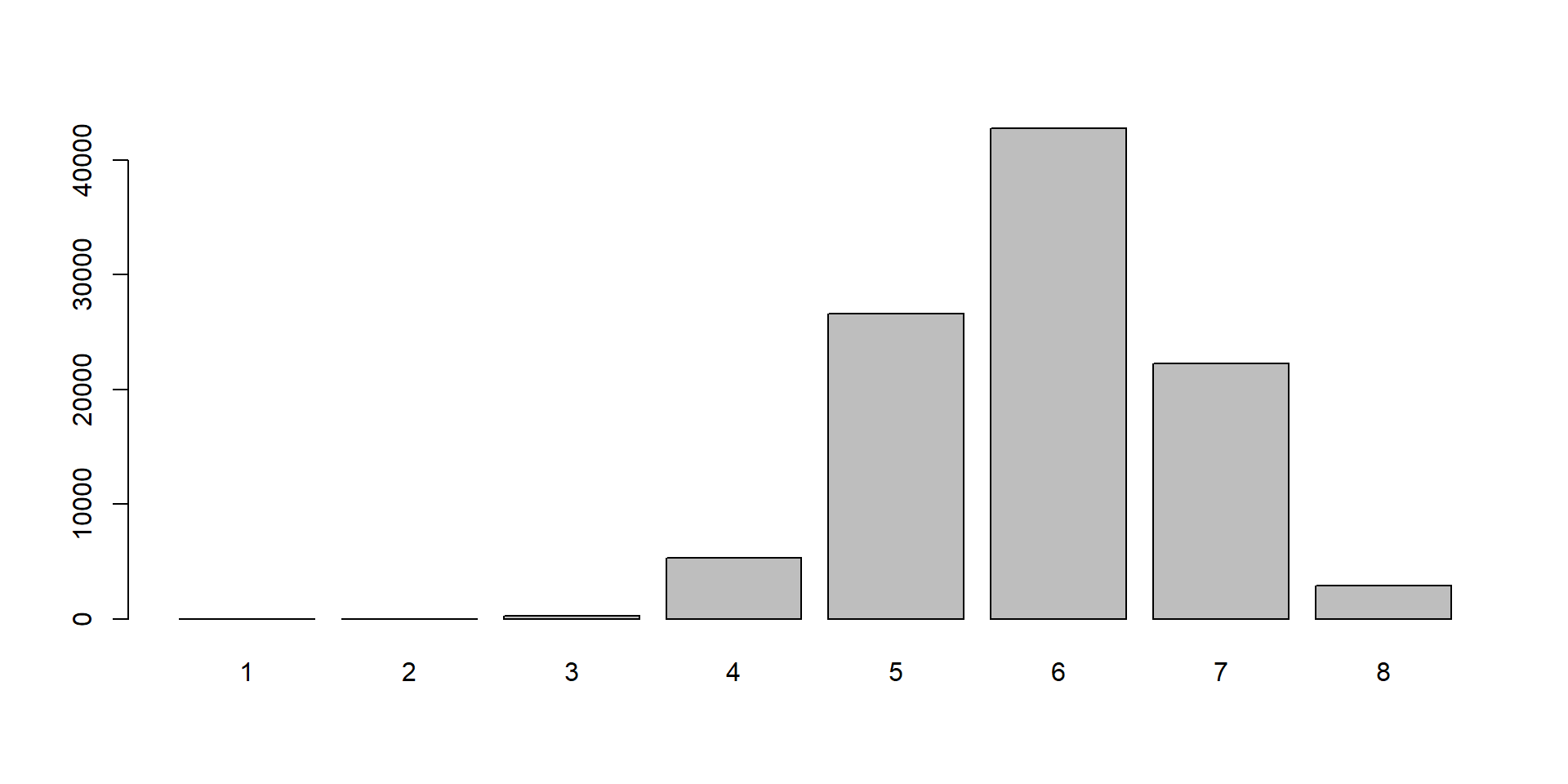 

barplot(tabulka)

Ak chceme odhady pravdepodobnosť (teda relatívne početnosti), použijeme funkciu prop.table. Jej vstupom je tabuľka vytvorená funkciou table.

prop.table(tabulka)

simulacie
      1       2       3       4       5       6       7       8 
0.00000 0.00005 0.00276 0.05291 0.26566 0.42759 0.22238 0.02865 

Ak nie je explicitne uvedené inak, úlohy budeme riešiť simuláciami.

Príklad 4: Americkí prezidenti

Marilyn vos Savant bola istý čas v Guinessovej knihe rekordov ako človek s najvyšším IQ. V rubrike Ask Marilyn odpovedala na rôzne otázky

Niektoré z nich boli matematické úlohy:

A high school student who hadn’t opened his American history book in weeks was dismayed to walk into class and be greeted with a pop quiz. It was in the form of two lists, one naming the 24 presidents in office during the 19th century in alphabetical order and another list noting their terms in office, but scrambled. The object was to match the presidents with their terms. The completely clueless student had to guess every time. On average, how many did he guess correctly?

Predpoklady:

• Predpokladajme, že jeho tipovanie odpovedí vyzerali tak, že každému prezidentovi priradil iné obdobie a každé takéto priradenie má rovnakú pravdepodobnosť.

• Namiesto 24 prezidentov budeme uvažovať všeobecnú verziu takéhoto testu s tipovania odpovedí s \(n\) položkami.

Zadania:

• Doplňte funkciu, ktorá generuje počet správnych odpovedí:

pisomka <- function(n){
  spravne <- 1:n  # bez ujmy na vseobecnosti
  odpovede <-     # doplnte
  return()        # doplnte
}

• Odhadnite strednú hodnotu počtu správnych odpovedí v písomke s prezidentami.

• Odhadnite závislosť strednej hodnotu počtu správnych odpovedí od počtu otázok \(n\).

• Vyslovte na základe tohto výsledku hypotézu o strednej hodnote a dokážte ju. Návod: definujte náhodné premenné \(X_i\) s hodnotami 0 a 1, ktoré vyjadrujú, či bola i-ta odpoveď správna.

• Odhadnite pravdepodobnosti počtu správnych odpovedí a zobrazte ich graficky pre písomku s 10 položkami. Pravdepodobnosti znázornite pre všetky celé čísla medzi 0 a 10 (vrátane toho, ktoré má nulovú pravdepodobnosť - ktoré to je a prečo?)

• Uvažujme rýchlu písomku tohto typu, v ktorej treba priradiť literárne diela k autorom, pričom obsahuje 5 položkami (všetci autori aj názvy diel sú rôzni). Za každú správnu odpoveď dostane študent jeden bod, za nesprávnu mínus jeden bod. Potrebuje získať kladný počet bodov. Aká je pravdepodobnosť, že sa mu to pri tejto stratégii podarí?

• Ako sa zmení pravdepodobnosť z predchádzajúcej otázky, ak písomka obsahuje len 4 položky?

• V písomke s piatimi položkami má Hviezdoslav dve diela (a teda v zozname autorov je dvakrát). Aká je pravdepodobnosť, že študent bude mať kladný počet bodov? (Na voľbu náhodnej permutácie to nemá vplyv, študent automaticky volí náhodné priradenie bez toho, aby vôbec čítal zadanie.)

Cvičenia

Príklad 5: Hádzanie nepravidelnými mincami

Funkcia sample sa dá pomocou parametra prob použiť na simulovanie hádzania rôznymi mincami (teda mincami, ktoré majú rôzne pravdepodobnosti padnutia hlavy a znaku). Defautne majú všetky hodnotay rovnaké pravdepodobnosti, môžeme ale zadať vlastné:

# 1 = hlava, 0 = znak

# pravidelna minca
sample(c(1, 0), size = 1)

[1] 0

sample(c(1, 0), size = 1, prob = c(0.5, 0.5))  # to iste ako bez parametra `prob`

[1] 1

# minca, na ktorej hlava padne s pp. 1/3
sample(c(1, 0), size = 1, prob = c(1/3, 2/3))  

[1] 1

Pomocou funkcie sapply vieme prehľadne simulovať hádzanie viacerými mincami, pričom každá je iná.

# 3 mince
# prva je pravidelna
# na druhej je pp. hlavy rovna 0.2
# na tretej je pp. hlavy rovna 0.9

sapply(c(0.5, 0.2, 0.9), function(p) sample(c(1, 0), size = 1, prob = c(p, 1 - p)))

[1] 0 0 1

Zadanie:

Máme \(n\) mincí, pričom \(i\)-ta minca je vyrobená tak, že na \(k\)-tej minci padne hlava s pravdepodobnosťou \(\frac{1}{2k+1}\). Hodíme všetkými mincami. Aká je pravdepodobnosť, že počet hláv bude párny?

Poznámka:

Príklad bol na súťaži Putnam Exam, kde bolo úlohou nájsť bez pomoci počítača analytické riešenie. Záujemcovia o matematické súťaže môžu skúsiť príklad riešiť aj takto - nie je to také ťažké (príklady na tejto súťaži majú tradične rôznu náročnosť).

Príklad 6: Ponožky

Máme \(n\) párov ponožiek. Zamiešame ich a vyberáme ich postupne bez toho, aby sme sa na ne pozerali. Ak vyberieme ponožku, ktorej pár sme už vybrali predtým, odložíme ich obidve nabok. Aká je stredná hodnota počtu nájdených párov po tom, čo sme vybrali \(k\) ponožiek?

Príklad 7: Streľba na terč

Dvaja strelci strieľajú striedavo na terč. Na začiatku si hodia mincu, kto bude v jednotlivých pokusoch strieľať ako prvý. Pravdepodobnosť zásahu pri prvom pokuse je pre strelca A rovná 0,4 a pre strelca B je rovná 0,5. Ak netrafí ani jeden, priblížia sa bližšie k terču, vďaka čomu sa pravdepodobnosti zásahu zvýšia o 0,05 a znovu strieľajú v tom istom poradí.

Ak netrafia, znovu sa priblížia, pričom pravdepodobnosti zásahu sa zvýšia o rovnakú hodnotu a znovu v tom istom poradí vystrelia na terč. Toto sa opakuje, kým niektorý z nich zasiahne terč. Aká je pravdepodobnosť, že terč bude trafený v \(n\)-tom kole (a aké hodnoty môže \(n\) nadobúdať)?

Príklad 8: Zákon schválnosti

Písomku písalo 20 študentov, opravené písomky sú v náhodnom poradí. Traja študenti si prišli pozrieť svoju písomku. Postupne berú do ruky opravené písomky, až kým nenájdu všetky tri hľadané písomky. Aká je pravdepodobnosť, že posledná hľadaná písomka bola na \(k\)-tom mieste a aké sú možné hodnoty \(k\)? Ktorá z nich má najväčšiu pravdepodobnosť?

Príklad 9: Oslavy narodenín

V istej firme na výrobu suvenírov sa pracuje každý deň vroku s výnimkou dní, v ktorých má niektorý zamestnanec narodeniny. Vtedy celá firma oslavuje a nepracuje sa. Ak sa pracuje, každý zamestnanec vyrobí v ten deň jeden suvenír.

Pre jednoduchosť zanedbajme priestupné roky (každý rok má teda 365 dní) a predpokladajme, že narodeniny majú počas roka rovnomerné rozdelenie a že firma nemá pred prijatím zamestnanca informáciu o dni jeho narodenia.

Koľko zamestnancov má mať firma, aby maximalizovala očakávaný počet suvenírov, ktoré sa vyrobia počas roka?