Normálne rozdelenie, CLV, podmienené pravdepodobnosti

Metódy riešenia úloh z pravdepodobnosti a štatistiky

Normálne rozdelenie \(\mathcal{N}(0,\sigma^2)\)

Už sme videli generovanie náhodných čísel:

set.seed(12345)
x_norm <- rnorm(10^4, mean = 10 , sd = 3) 
head(x_norm) # head = zaciatok vektora, analogicky tail = koniec
[1] 11.756586 12.128398  9.672090  8.639508 11.817662  4.546132
hist(x_norm)

Hustota a distribučná funkcia

dnorm - hustota (density)

curve(dnorm, from = -5, to = 5) # jeden zo sposobov kreslenia grafov
curve(dnorm(x, mean = 0.5, sd = 1.5), from = -5, to = 5, col = "red", add = TRUE)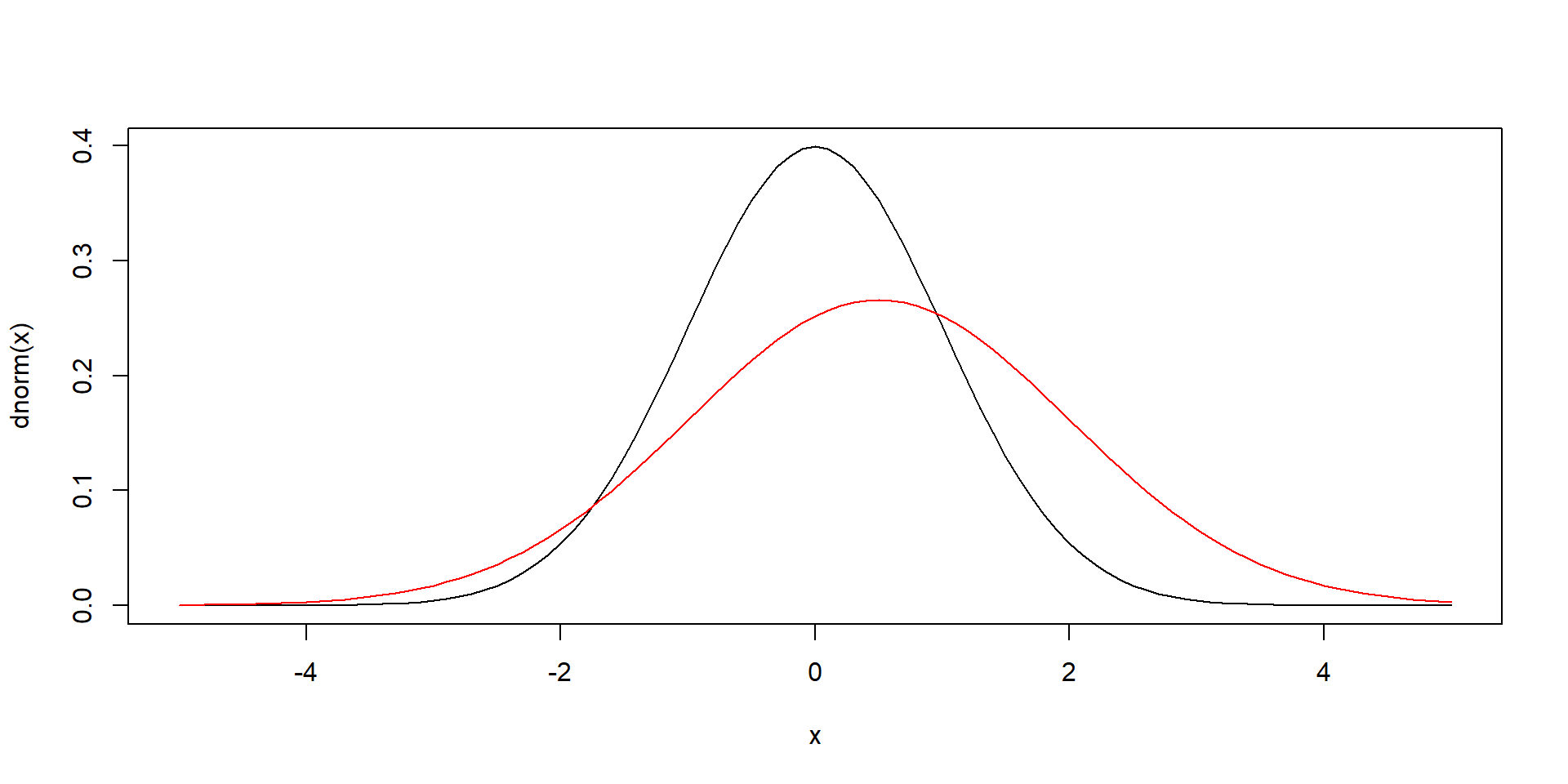

pnorm - distribučná funkcia (probability distribution function)

curve(pnorm, from = -5, to = 5) # jeden zo sposobov kreslenia grafov
curve(pnorm(x, mean = 0.5, sd = 1.5), from = -5, to = 5, col = "red", add = TRUE)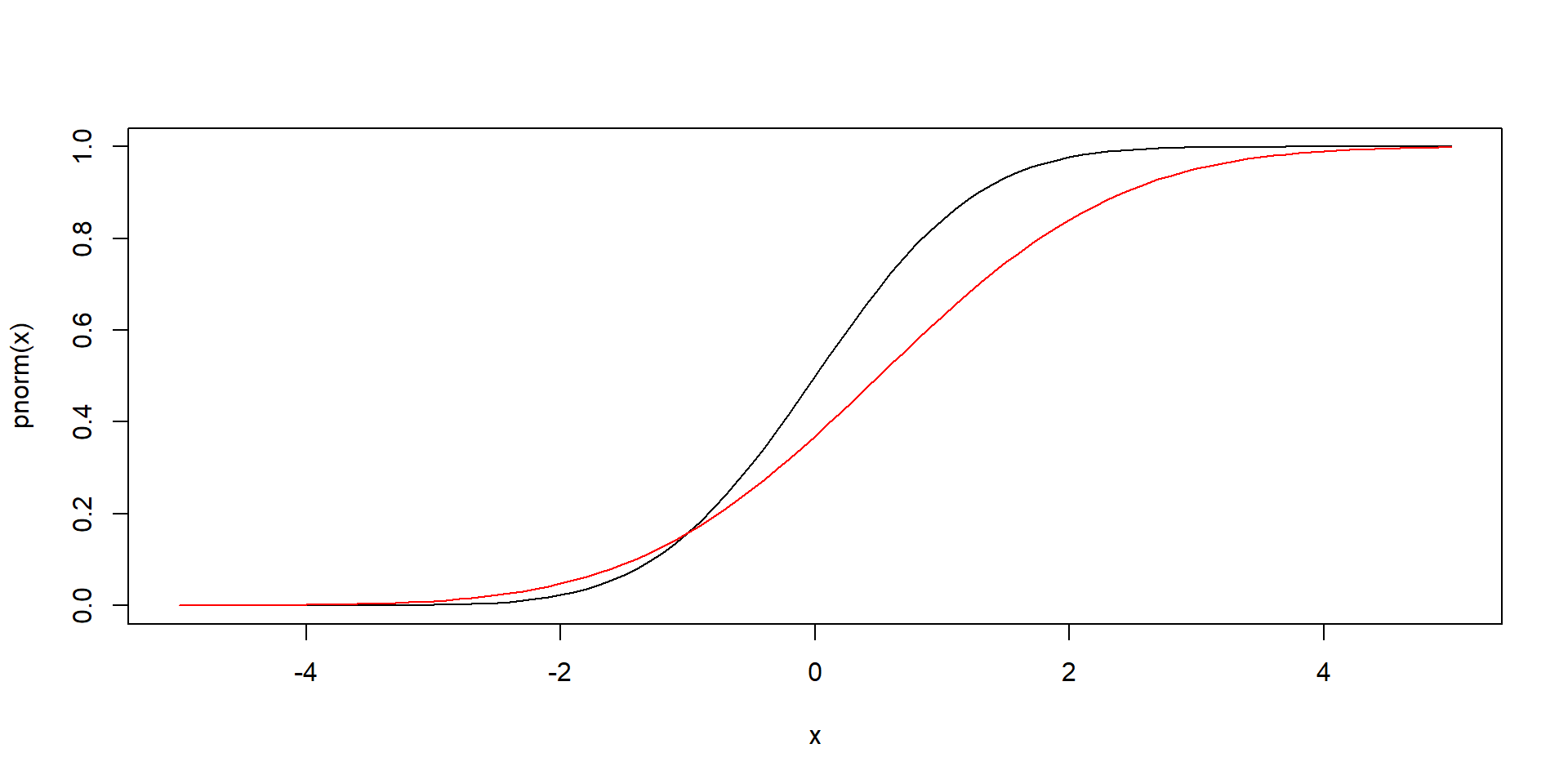

Kontrolná otázka: Čomu sa rovná nasledovná hodnota?

pnorm(0)

Príklad 1.

  • Aká je pravdepodobnosť, že náhodná premenná \(\mathcal{N}(0, 4)\) nadobudne hodnotu z intervalu \((1, 2)\)?

  • Náhodná premenná \(X\) má normálne rozdelenie s nulovou strednou hodnotou a zadanou disperziou. Nakreslite graf funkcie, ktorej hodnota sa rovná pravdepodobnosti, že takáto náhodná premenná nadobudne hodnotu z intervalu \((1, 2)\).Nezávislou premennou je disperzia náhodnej premennej \(X\).

Súčet a priemer náhodných premenných s normálnym rozdelením

Príklad 2. Výška škody pri dopravnej nehode má normálne rozdelenie so strednou hodnotou 19 400 a štandardnou odchýlkou 5 000. Škody v jednotlivých nehodách sú nezávislé. Vyberieme náhodne údaje o 25 nehodách. Aká je pravdepodobnosť, že priemerná škoda bude vyššia ako 20 000?

Možnosti: (A) 0.01 (B) 0.15 (C) 0.27 (D) 0.33 (E) 0.45

Doplňujúca otázka: Vyjadrite túto pravdepodobnosť pomocou distribučnej funkcie normalizovaného normálneho rozdelenia \(\mathcal{N}(0,1)\)

Centrálna limitná veta

Základná myšlienka: Rozdelenie súčtu nezávislých náhodných premenných s rovnakým rozdelením - s konečnou strednou hodnotou a disperziou - sa pri veľkom počte sčítancov podobná na normálne rozdelenie

Ukážka:

sucet_exp_simulacia <- function(str_hod, pocet_scitancov, pocet_simulacii)
  replicate(pocet_simulacii, sum(rexp(pocet_scitancov, rate = 1/str_hod)))

hist(sucet_exp_simulacia(str_hod = 1, pocet_scitancov = 3, pocet_simulacii = 1000)) # X_1 + X_2 + X_3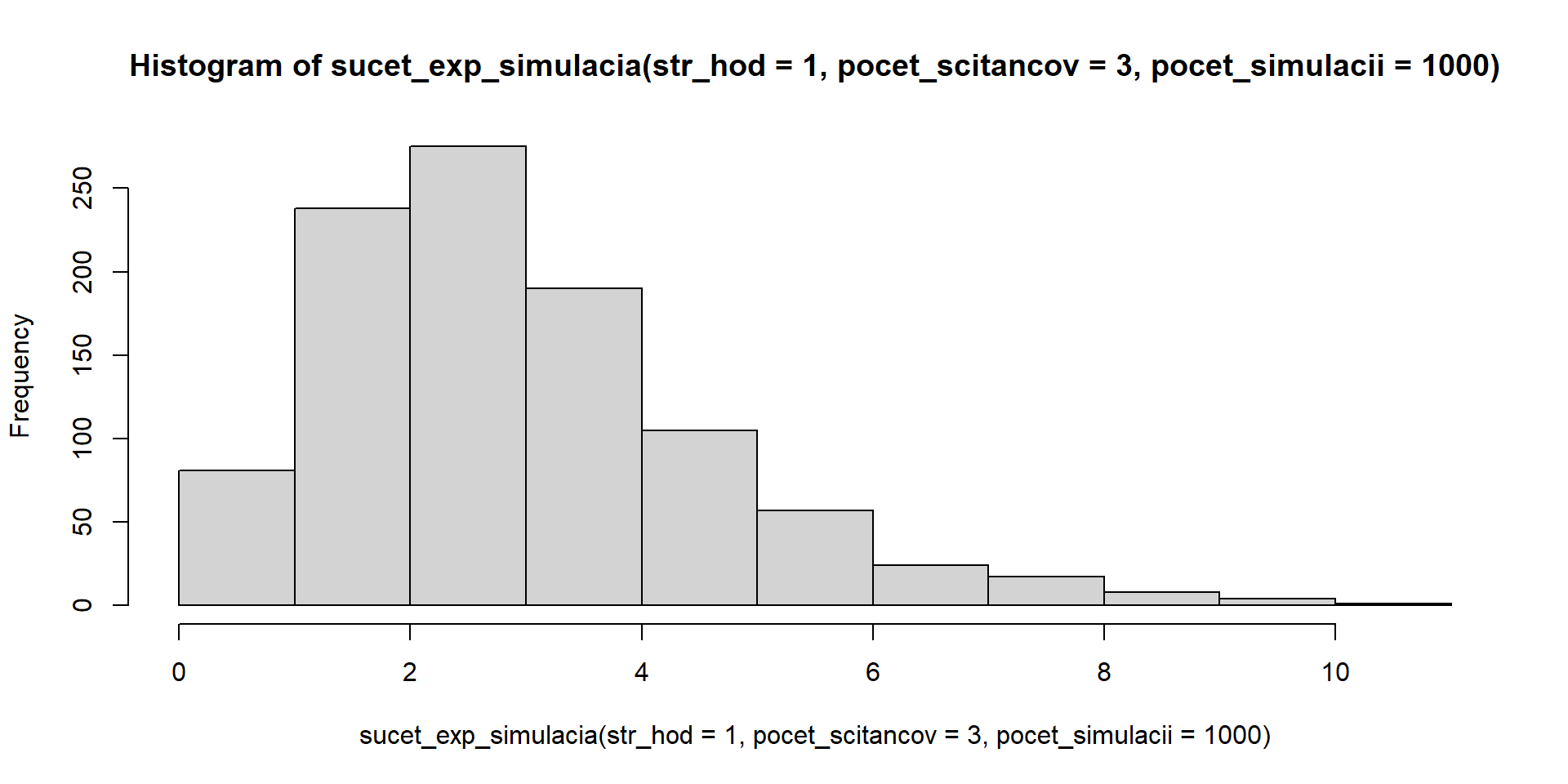

hist(sucet_exp_simulacia(str_hod = 1, pocet_scitancov = 100, pocet_simulacii = 1000)) # X_1 + ... + X_100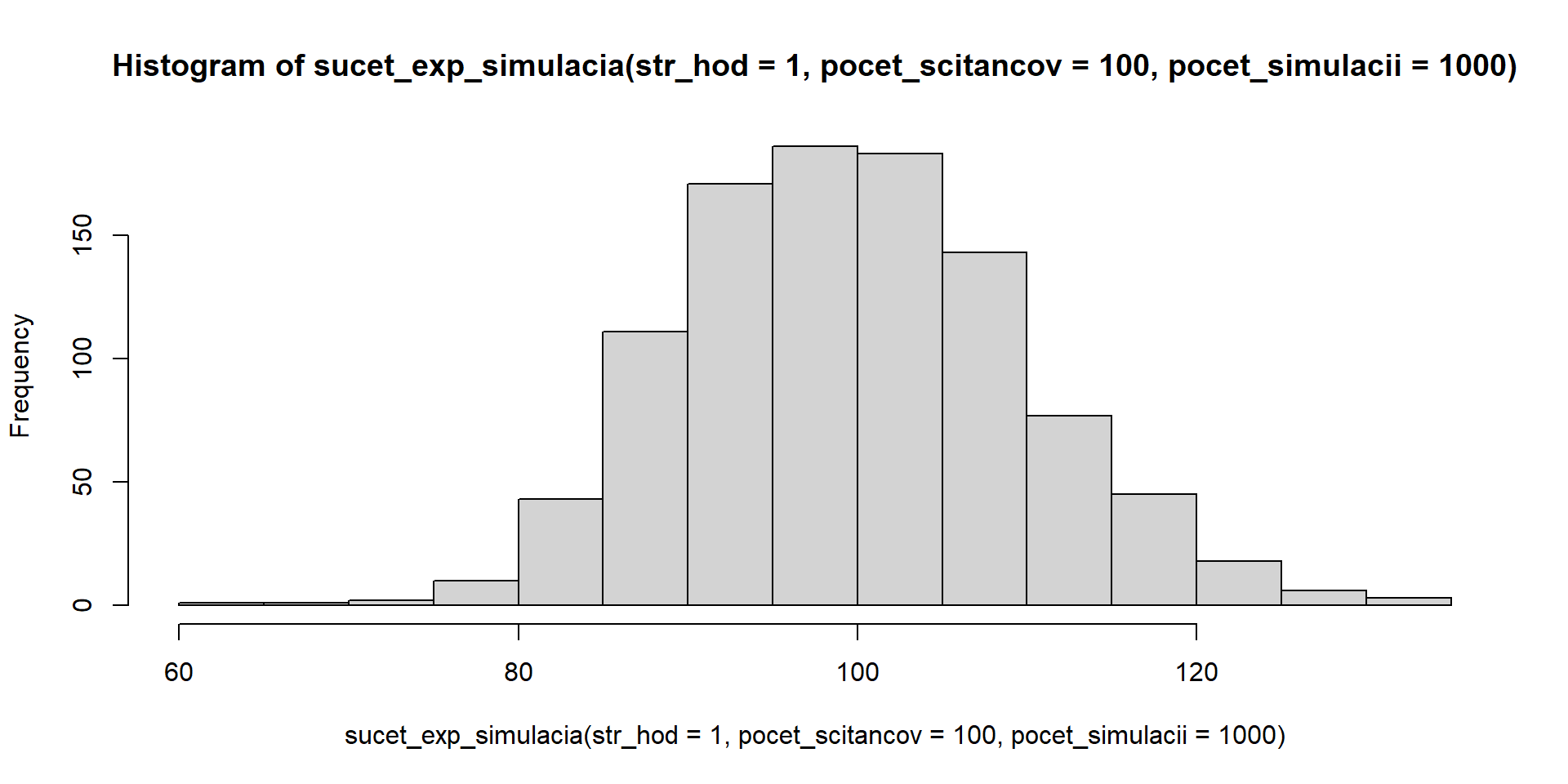

Príklad 3. Poistné plnenia pre určité zdravotné poistenie sú nezávislé s exponenciálnym rozdelením so strednou hodnotou 1000. Výška poistného je o 100 vyššia ako očakávaná hodnota poistného plnenia. Uzavretých bolo 100 poistení. Aká je pravdepodobnosť, že výdavky poisťovne budú vyššie ako príjmy?

Možnosti: (A) 0.001 (B) 0.159 (C) 0.333 (D) 0.407 (E) 0.460

Príklad 4. Vek poistencov sa udáva zaokrúhlený na 5 rokov. Vieme, že rozdiely medzi presným a zaokrúhleným vekom majú rovnomerné rozdelenie na intervale (−2.5, 2.5) a pre jednotlivých poistencov sú nezávislé. Zo 48 náhodne vybraných údajov sa vypočíta priemerný vek. Aká je pravdepodobnosť, že sa od skutočného priemerného veku týchto poistencov líši menej ako o štvrť roka?

Možnosti: (A) 0.14 (B) 0.38 (C) 0.57 (D) 0.77 (E) 0.88

Príklad 5. Polícia prijala 100 policajtiek. Tým, ktoré zostanú v polícii až do dôchodku, mesto vyplatí určitú sumu. Ak budú v čase odchodu do dôchodku vydaté, takú istú sumu dostane aj manžel. Predpokladáme, že je známe:

  • Pravdepodobnosť toho, že policajtka zostane na polícii do dôchodku, je 0.4
  • Za predpokladu, že dostane do dôchodku, pravdepodobnosť toho, že v tom čase nebude vydatá, je 0.25.
  • Nezávislosť obidvoch veličín (zostane do dôchodku, bude vydatá) pre jednotlivé policajtky

Zaujíma nás počet výplat dohodnutej sumy (policajtkám a ich manželom). Aká je pravdepodobnosť, že ich nebude viac ako 90?

Možnosti: (A) 0.60 (B) 0.67 (C) 0.75 (D) 0.93 (E) 0.99

Podmienená pravdepodobnosť

  • Príklad o policajtkách obsahoval v skutočnosti podmienené pravdepodobnosti - za predpokladu, že dostane do dôchodku, pravdepodobnosť toho, že v tom čase nebude vydatá je \(\mathbb{P}(\textrm{nebude vydatá} | \textrm{zostane do dôchodku})\)

  • Podmienené pravdepodobnosti budeme potrebovať pri klasifikácii dát, zopakujeme si ich použitie:

Príklad 6.

  • Dvaja opití kamaráti vychádzajú z krčmy, ktorá má pri vchode nápis HAPPY HOUR.
  • Jeden z nich náhodne odlepí dve písmená (s rovnakou pravdepodobnosťou pre každú dvojicu).
  • Druhý ich prilepí naspäť, ale náhodne, nepozerá sa, či ich vracia správne.
  • Aká je pravdepodobnosť, že nápis HAPPY HOUR zostane zachovaný?

Príklad 7.

  • V meste sú dve taxislužby. Jedna má 85 zelených áut, druhá má 15 modrých áut.
  • Počas hmlistého večera jazdili všetky taxíky. Jeden zrazil mladého muža. Ten neskôr vypovedal, že taxík bol modrý.
  • Polícia vyskúšala, nakoľko je schopný rozoznať farbu v podobných podmienkach, ako boli v ten večer, a zistila, že farbu dokáže určiť správne v 75 percentách prípadov.
  • Aká je pravdepodobnosť, že muž bol naozaj zrazený modrým taxíkom?

Príklad 8.

  • Batožina je prepravovaná postupne troma leteckými spoločnosťami.
  • Pravdepodobnosť, že prvá spoločnosť stratí batožinu je 0,1. Pre druhú spoločnosť je táto pravdepodobnosť 0,05 a pre tretiu 0,15.
  • Batožina sa stratila. Aká je pravdepodobnosť, že ju stratila \(i\)-ta spoločnosť?

Poznámky:

  • Máme tu podmienené pravdepodobnosti: “pravdepodobnosť, že spoločnosť stratí batožinu” je podmienená pravdepodobnosť “pravdepodobnosť, že spoločnosť stratí batožinu, ak ju prevzala do prepravy”.
  • Skúška správnosti: Batožina sa stratila, teda súčet pravdepodobností, že ju stratila \(i\)-ta spoločnosť, musí byť 1.