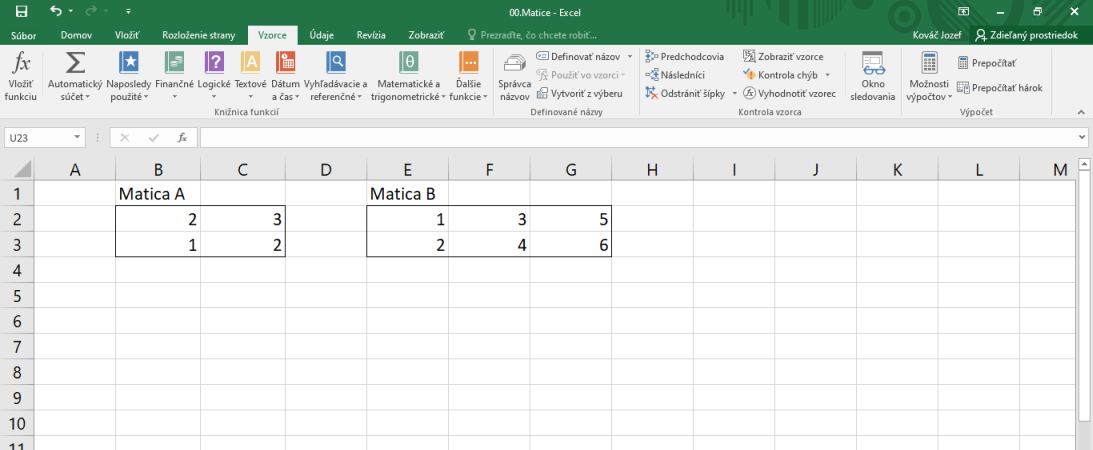
Predpokladajme, že máme maticu $ A= \begin{pmatrix} 2 & 3 \\ 1 & 2 \end{pmatrix} $ a maticu $ B= \begin{pmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{pmatrix} $. V exceli si tieto matice dáme napríklad do políčok B2:C3, resp. E2:G3.

Keď chceme spraviť nejakú maticovú operáciu, v prvom rade je dôležité uvedomiť, aké rozmery bude mať výsledok. Napríklad ak chceme urobiť operáciu $A+A$, tak výsledok bude mať rozmery $2\times 2$. Ak chceme výsledok zapísať do políčok B6:C7, tak si tieto políčka vyznačíme a do vzorcového riadku napíšeme =B2:C3+B2:C3 a stlačíme Ctrl+Shift+Enter - ak by sme dali iba Enter, tak to spravidla vráti chybu. Pozor, Ctrl+Shift+Enter treba dávať aj vtedy, keď robíme maticovú operáciu, ktorej výsledok má rozmery $1\times 1$ (výsledok je síce iba jedna bunka, ale dopracovali sme sa k nemu cez maticové operácie).

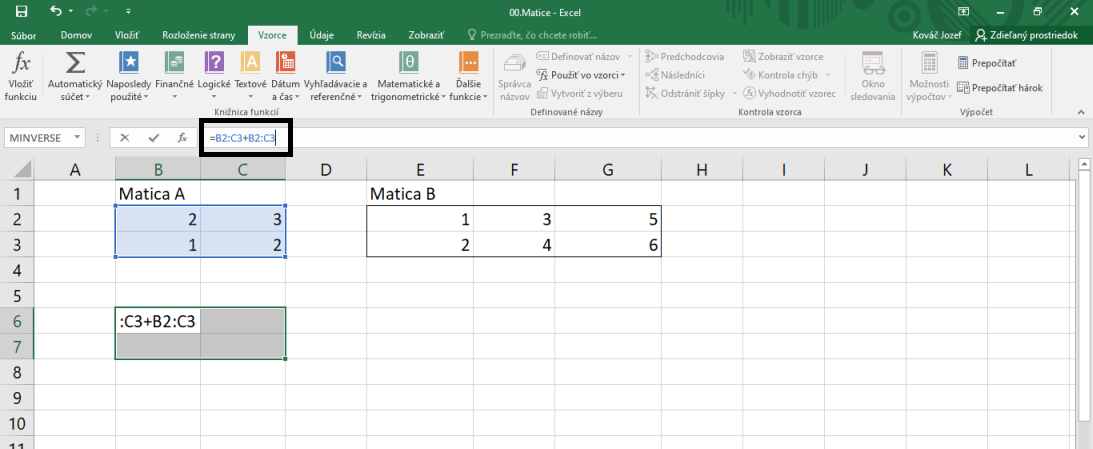
Pri kliknutí na ľubovoľné z políčok B6:C7 potom vo vzorcovom riadku vidíme {=B2:C3+B2:C3} (tými kučeravými zátvorkami sa odlišuje maticová operácia od normálnej).

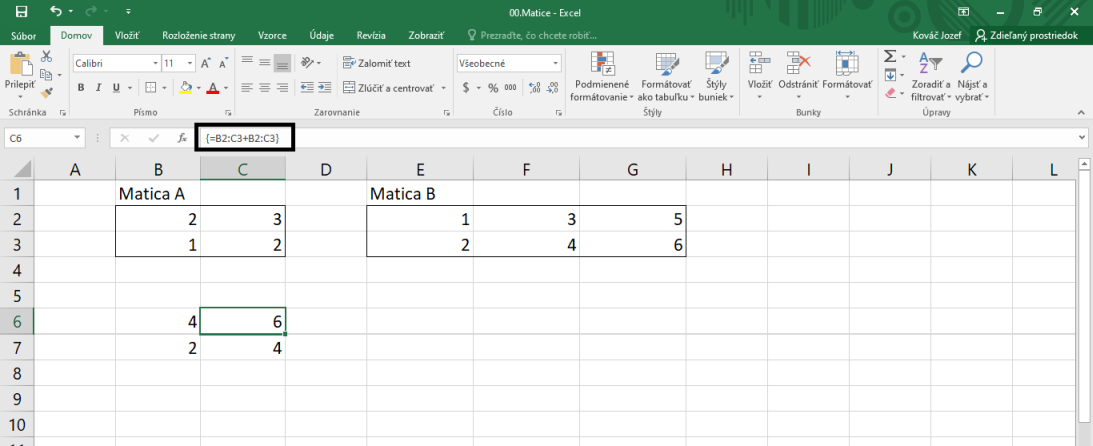
V prípade, že sa nám nechce stále vypisovať "B2:C3", vieme si tieto bunky hromadne uložiť pod nejakým menom (napr. A) - stačí vyznačiť tieto bunky a dať Vzorce → Definovať názov a vyplniť názov. Keď potom vo vzorcoch napíšeme "A", Excel bude pod týmto automaticky rozumieť políčka B2:C3.

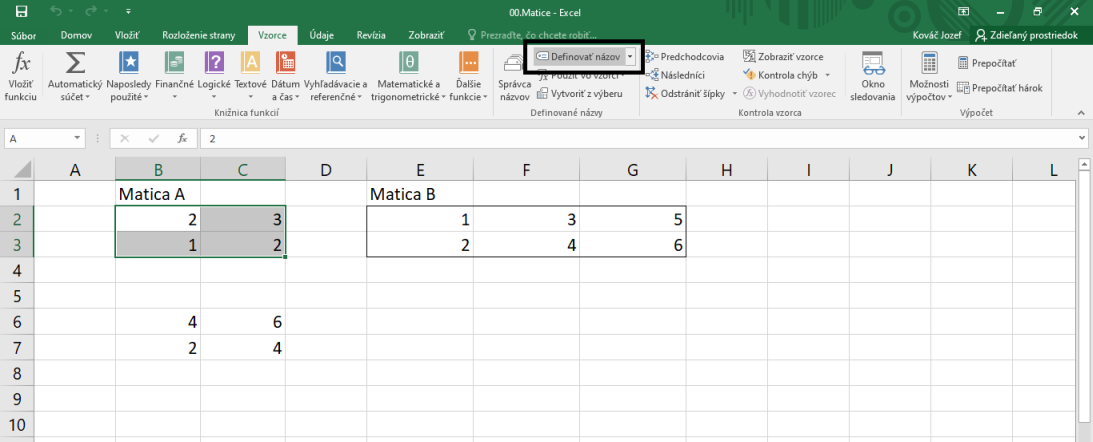
Takisto si môžeme pre jednoduchosť označiť políčka E2:G3 písmenom B. Ak chceme tieto dve matice vynásobiť, v Exceli na to existuje funkcia MMULT. Keďže výsledok bude matica typu $2\times 3$, vyznačíme políčka E6:G7 a do vzorcového riadku napíšeme =MMULT(A,B) a stlačíme Ctrl+Shift+Enter. Pozor, =A*B spraví niečo iné.

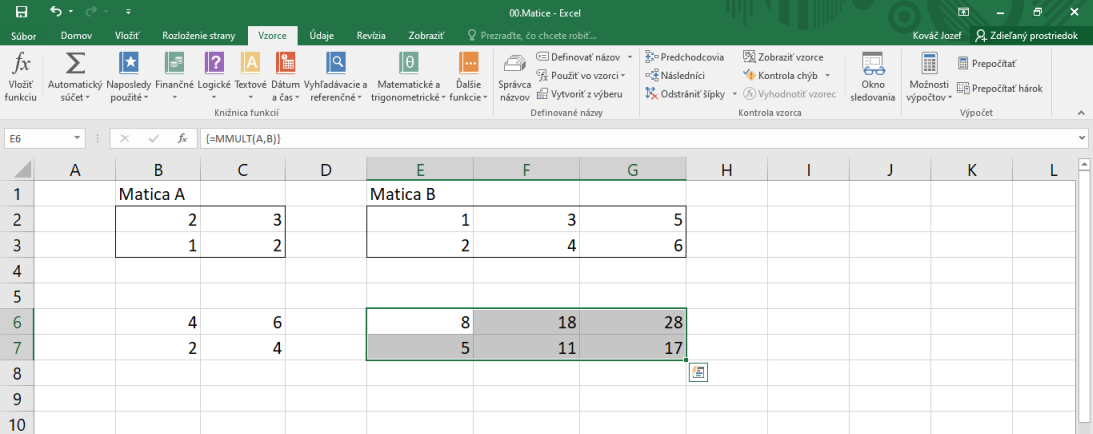
Ďalšie maticové funkcie, ktoré sa môžu zísť sú transpozícia (napr. =TRANSPOSE(A)) a inverzia (napr. =MINVERSE(A)).