Research in the field of dynamic financial and portfolio management models is primarily focused on dynamic stochastic programming in order to maximize utility due to the dynamically changing weights of individual portfolio components. We use methods based on the solution of the Hamilton-Jacobi-Bellman partial differential equation and its suitable transformations. We propose efficient and stable numerical schemes for solving underlying equations. The results are applied mainly in the field of dynamic optimal management of retirement pension funds.

The research is focused on theoretical and computational study of the dynamics of complex fluids and its applications to other areas such as mechanical and chemical engineering, materials science and geophysics. Mathematical aspects of research include the theory of asymptotic scaling and reduction of underlying differential equations, the theory of stability and bifurcations, perturbation and asymptotic methods, and numerical methods for partial differential equations.

Data envelopment analysis (DEA) is a non-parametric method in operations research for measuring the relative efficiency of decision making units based on mathematical programming techniques. In our research we focus on applying the theory and methods of convex optimisation to provide a unified analysis of DEA models, on studying the environmental DEA models and on designing computational methods for large-scale DEA models. We also work on implementing codes for a large variety of linear and non-linear DEA models and related problems.
The research is focused on qualitative and numerical aspects in the field of the dynamics modeling of curvature driven flows of plane closed curves. We also focus on the study of various nonlocal geometric flows preserving geometric quantities, such as area or length. Special attention is paid to the design of numerical schemes that are optimal in terms of discretization points distribution on evolving varieties. Finally, we study applications in the field of phase interface dynamics and dislocation loops in materials research.
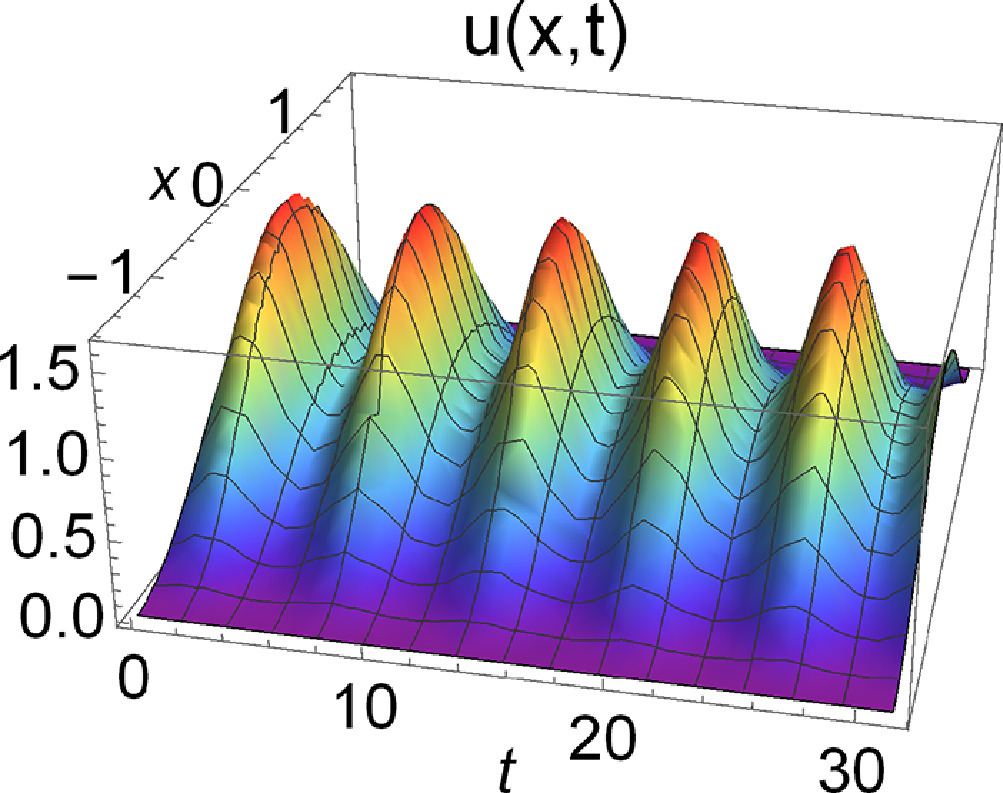
The research is focused on the study of properties of solutions of nonlinear diffusion equations and systems, as well as problems with nonlinear and dynamical boundary conditions. Besides questions related to the existence and uniqueness, we investigate mainly asymptotic properties of solutions.

The aim of the research is to provide qualitative and numerical analysis of solutions of direct and inverse variational problems, which can be solved using modern methods of conic programming. We focus on the analysis of of strong duality properties of primal and dual pairs in case of conic programming problems.

Gene expression is a set of processes by which the information encoded in a genetic template is used to make active molecules, especially proteins. The development of new technologies enabling the measurement of gene expression at the level of individual molecules continually motivates the research of mathematical models describing the gene expression dynamics. At our department, we primarily focus on the methodology using differential equations and stochastic simulations.
The aim of the research is to estimate the public health impact of changes in vaccination indicators on the epidemiological situation. In our research, we focus on highly contagious diseases and their epidemic threats in EU countries. We pay particular attention to two main indicators of vaccination: the vaccination rates and the timeliness of vaccination. Using mathematical and statistical models, we investigate several possible vaccination scenarios and then we evaluate their public health, social and economic impact. We also forecast the epidemiological situation using deterministic and stochastic models and measure the social impact on individuals and society through QALY and DALY indicators.
Mathematical models in evolutionary genetics, cell biophysics, and animal physiology help to understand the principles of evolution and functionality of biological species on a macroscopic and microscopic scale. In our research, we study telomeric DNA, which is involved in the regulation of cell aging, the population growth in yeast and the regulation of biorhythms under the influence of the external environment. In addition, our research deals with a number of interesting problems on the edge of current mathematical knowledge, which we study thoroughly.
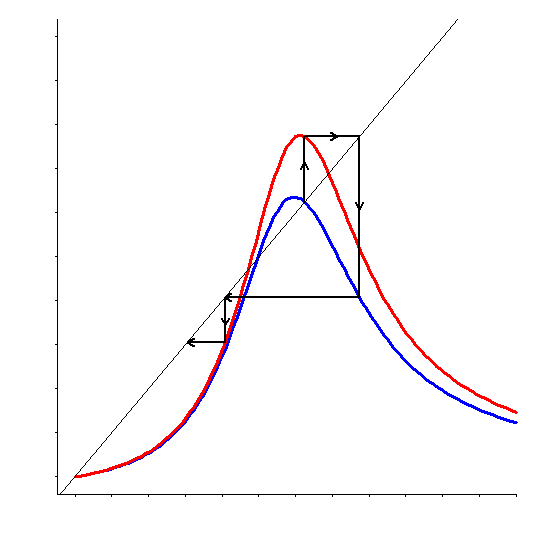
Our research is focused on random dynamical systems generated by continuous self-mappings of an interval and their applications, for example, in population dynamics. We are interested in problems concerning complex behavior of these systems. Under certain conditions, the system stabilizes at some kind of equilibrium, hence its behavior is simple in some sense. Other systems may exhibit extremely unstable behavior which can be considered chaotic. For characterization of this complexity, we use notions of chaos known from the theory of discrete dynamical systems.

In the research we focus on the qualitative and numerical analysis of partial differential equations describing the derivative price changes of the underlying assets, such as interest rate derivatives or equities. We pay special attention to asymptotic and perturbation analysis of solutions depending on parameters and model calibrations for real market data. We also examine the problems leading to the solution of complementarity problems and variational inequalities appearing by valuation of American types of derivatives with early exercise.
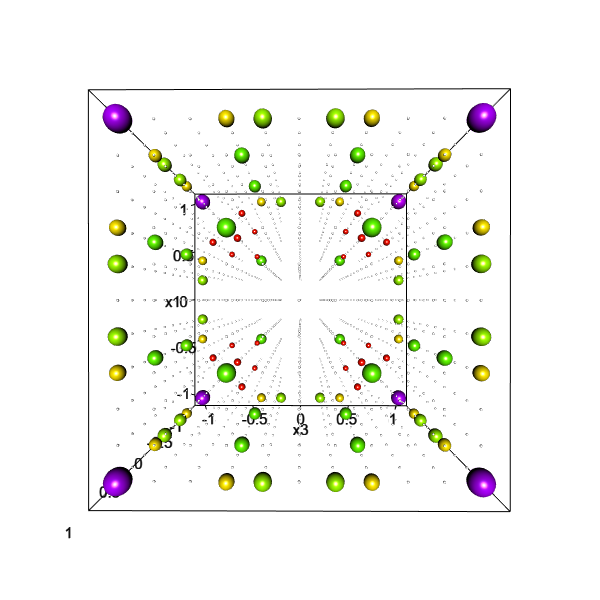
D-optimal approximative design of experiment for a cubic regression model on cube
Optimal design of experiments is a discipline of mathematical statistics that deals with methods of planning of an experiment in order to obtain as much information as possible within specified constraints on available resources, or to ensure the required data quality at the lowest possible cost. The results of the research in this discipline are applicable in empirical sciences, medicine, industry, agriculture, but also, e.g., in population surveys. The founder of the school of optimal design of experiments at FMPI is prof. RNDr. Andrej Pázman, DrSc., who is also one of the leading figures in this field of research from the global perspective.

Our research is focused on the analysis of special classes of probability distributions. New statistical methods for distributions from these classes are suggested and theoretically characterized, namely, parameter estimations, goodness of fit tests, and parametric and non-parametric statistical inference. This statistical apparatus is then applied to specific problems in metrology, insurance and financial mathematics, linguistics and demography. As a part of the project, computational methods and algorithms are constructed for these statistical procedures.
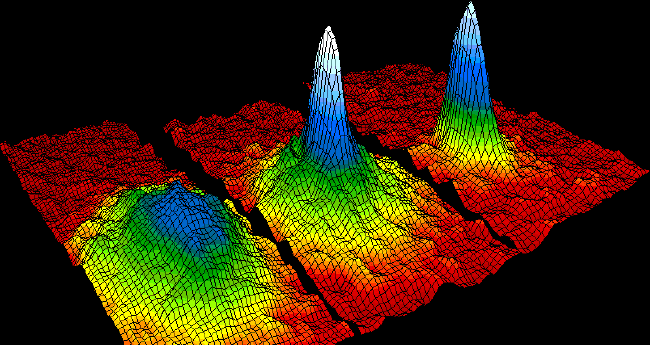
The stability of solutions of nonlinear differential equations has an important role in many applications in geophysics, astrophysics, materials engineering, fluid flow mechanics, condensed matter physics, evolutionary biology and in many other fields. In addition to identifying stable states, questions about the changes in stability under the influence of system parameter's changes are also important. In the linear approximation, the stability is characterized by the spectrum of the corresponding operator. In our research we focuses on the study of qualitative spectrum changes, especially via the Krein signature, which identifies potentially unstable modes of Hamiltonian systems.

In our research team, we primarily focus on the quantitative analysis of pension systems. In the case of the accumulation phase of saving systems, we study various dynamic portfolio management techniques and we also deal with the problem of finding the optimal investment strategy that maximize the future utility of savers. In the decumulation phase of pension schemes, we examine the impact of risk factors on the future old-age annuity benefits and we also analyze other possible payout products. Our goal is to advance research on mathematical modeling of funded pension schemes, develop dynamic control strategies for savings management and publish applicable results for the old-age pension scheme in Slovakia.