Black-Scholesov vzorec, analýza citlivosti na parametre
:: Nie sme tu pre srandu králikov ::

| Pred nejakým časom som dostala takéto pekné oznamko s mottom "Nie sme tu pre srandu králikov". Ale ani príklady na precvičenie tu nie sú pre srandu králikov. Tak sa na niektoré pozrime:
|
:: Cena európskej call a put opcie ::
- Call opcia:
function [v]=call(S,E,r,tau,sigma) d1=(log(S/E)+(r+0.5*sigma^2)*tau)/(sigma*sqrt(tau)); d2=(log(S/E)+(r-0.5*sigma^2)*tau)/(sigma*sqrt(tau)); v=S*normcdf(d1)-E*exp(-r*tau)*normcdf(d2)
- Put opcia: dá sa oceniť napríklad pomocou put-call parity.
- Z linearity Black-Scholesovej rovnice vyplýva, že aj je koncová podmienka derivátu lineárnou kombináciou call a put opcií, rovnakou lineárnou kombináciou cien call a put opcií dostaneme cenu tohto derivátu.
:: Cvičenia (1) ::
- Vypočítajte cenu európskej call opcie s expiráciou o pol roka, ktorej expiračná cena je 50 USD. Dnešná cena akcie je 41 USD,
jej volatilita je 0.3. Úroková miera je pol percenta.
- Upravte funkciu call tak, aby ste mohli pracovať s vektorovými argumentmi a kresliť napríklad takého grafy:
S=0:0.1:100; plot(S,call(S,50,0.01,1,0.25));
Nakreslite graf s cenou akcie na x-ovej osi, na ktorom bude payoff call opcie a jej ceny pre niekoľko časov do expirácie.
Ukážka výstupu: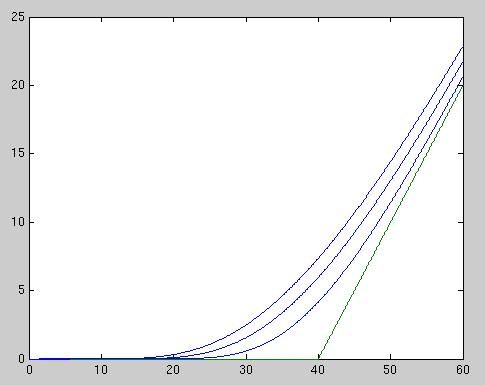
- Napíšte funkciu, ktorá vracia hodnotu putu a zobrazte podobný graf pre put opciu.
- Zostrojte stratégiu typu kondor pre zvolené parametre. Znovu nakreslite
s cenou akcie na x-ovej osi, na ktorom bude payoff stratégie a jej ceny pre niekoľko časov do expirácie.
- Dokážte, že ak V je riešením Black-Scholesovej PDR, tak aj
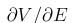 je riešením.
Použite túto vlastnosť na výpočet ceny binárnej opcie, t. j. opcie s payoffom
je riešením.
Použite túto vlastnosť na výpočet ceny binárnej opcie, t. j. opcie s payoffom
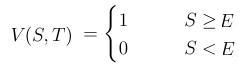
:: Citlivosť na parametre - greeks ::
-
Greeks - derivácie ceny opcie podľa jednotlivých parametrov:
- delta - derivácia podľa ceny akcie
- gama - druhá derivácia podľa ceny akcie
- vega - derivácia podľa volatility
- theta - drivácia podľa času (t.j. mínus derivácia podľa času zostávajúceho do expirácie)
- rho - derivácia podľa úrokovej miery
- Derivácie pre call opciu:
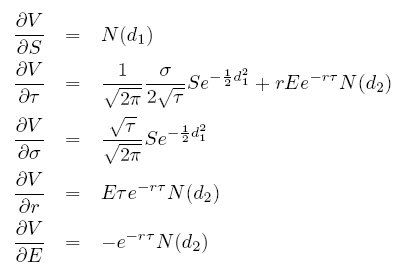
:: Cvičenia (2) ::
- Nakreslite graf závislosti delty call opcie od aktuálnej ceny akcie. Nakreslite do jedného grafu deltu pre rôzne časy do expirácie. V čom sa líšia?
- Pri odvodení Black-Scholesovho vzorca vystupuje delta ako počet akcií, ktoré kúpime pri hedžovaní jednej predanej opcie. Na základe tejto interpretácie vysvetlite priebeh grafu z predchádzajúcej úlohy - znamienko, monotónnosť, priebeh pre tau blízke nule.
- Nakreslite graf závislosti gamy call opcie od aktuálnej ceny akcie. Nakreslite do jedného grafu gamu pre viaceré expiračné ceny a pre rôzne časy expirácie. V čom sa líšia? Gama je derivácou delty podľa S, vyjadruje teda zmenu delty pri zmene ceny akcie. Interpretujte závislosť gamy od ceny akcie na základe získaných grafov a interpretácie delty ako počte kúpených akcií pri hedžovaní jednej predanej call opcie.
- Ako sa líši delta call a put opcie? Ako sa líši ich gama?
- Uvažujme nasledujúce hodnoty parametrov (výpočet zo stránky
http://www.sitmo.com/live/OptionVanilla.html):
Theta je tu derivácia podľa času do expirácie, t.j. tau.
Vidíme, že cena príslušnej call opcie je 10.4505 USD, cena put opcie je 5.5735 USD. Aká by bola cena tejto opcie, ak by cena akcie bola 99 USD namiesto 100 USD? Ak by cena akcie bola 101 USD? Vypočítajte približnú hodnotu pomocou greeks a potom ju porovnajte s presnou. - Čomu by sa približne rovnala cena put opcie nasledujúci deň, ak by cena akcie zostala rovnaká? Porovnajte s presnou hodnotou.
:: Implikovaná volatilita ::
- Implikovaná volatilita je taká hodnota volatility sigma, ktorej dosadením do Black-Scholesovho vzorca dostaneme trhovú cenu opcie.
- Cena call opcie je rastúcou funkciou volatility. Ak volatilita konverguje k nule, limita ceny call opcie je max(0,S-E*exp(-r
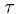 )). Ak, naopak, volatlita ide do nekonečna, limita ceny opcie je aktuálna cena akcie S. Ak je teda trhová cena call opcie z intervalu (max(0,S-E*exp(-r
)). Ak, naopak, volatlita ide do nekonečna, limita ceny opcie je aktuálna cena akcie S. Ak je teda trhová cena call opcie z intervalu (max(0,S-E*exp(-r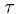 )),S), tak implikovaná volatilita existuje a je jednoznačne určená.
)),S), tak implikovaná volatilita existuje a je jednoznačne určená.
- Je viacero možností, ako implikovanú volatilitu prakticky vypočítať, tu je jedna z nich:
Definujeme funkciu rozdiel.m, ktorej parametrom je sigma a vracia rozdiel medzi skutočnou a Black-Scholesovou cenou. Ostatné parametre výpočtu sú definované ako globálne premenné:
Príklad použitia: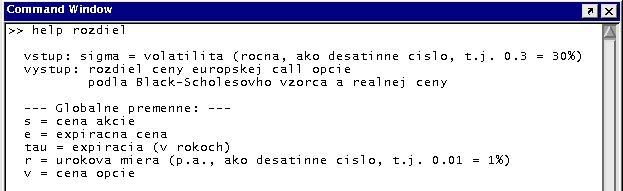
global s; global e; global tau; global r; global v; s=85.2; e=80; r=0.01; tau=0.5; v=11.12; % hladame nulovy bod tejto funkcie sig=0.01:0.01:0.5; plot(sig,rozdiel(sig),sig,0*ones(length(sig))); fzero(@rozdiel,0.4);
Výstup:
:: Ďalšie príklady na precvičenie ::
- Porovnajte reálne ceny opcií s teoretickými hodnotami z Black-Scholesovho vzorca. Použite volatilitu odhadnutú z historických dát.
- Vypočítajte hodnotu stratégie, ktorá pozostáva z kúpy call opcie s nízkou expiračnou cenou
a predaja call opcie s vyššou expiračnou
cenou s tou istou dobou splatnosti. Výpočet ceny stratégie realizujte pre nasledovné dáta: cena akcie
55 USD, volatilita akcie 0.4, úrok
jeden a pol percenta, expiračná doba 3 mesiace,
expiračné ceny sú 50 a 60 USD.
- Vypočítajte greeks pre put opcie. Ktorá derivácia nemá jednoznačne určené znamienko? Uveďte príklad parametrov, pre ktoré je kladná a príklad parametrov, pre ktoré je záporná.
- Implikovaná volatilita pre put opcie: Pre aký interval cien put opcií existuje? Je v týchto prípadoch určená jednoznačne? Zrealizujte výpočet implikovanej volatility pre konkrétnu put opciu.
- Uvažujme call opciu na s expiračnou cenou 15 USD, ak dnešná cena akcie je 9 USD. Pre ktoré z nasledujúcich cien opcie -- 2 USD, 5 USD, 7 USD, 10 USD, 15 USD -- existuje implikovaná volatilita? Pre ktorú z nich je implikovaná volatilita najvyššia?
- Zvoľte si akciu a z historických dát jej cien odhadnite histrickú volatilitu. Potom odhadnite implikovanú volatilitu z cien opcií na túto akciu a porovnajte ich.
- V súbore msft.txt je vývoj cien akcie firmy MSFT a opcií na tieto akcie. Formát:
Zvoľte si deň a načítajte dáta o vývoji akcie počas tohto dňa. Zvožte si akciu a načítajte dáta o vývoji ceny tejto opcie v danom dni. V súbore msft-call-apr-25.txt sú tieto hodnoty pre call opciu s expiračnou cenou 25 USD a expiráciou v apríli (bid cena akcie, ask cena akcie, bid cena opcie, ask cena opcie).
Zobrazte priebeh parametrov delta a gama počas zvoleného dňa.
- Dokážte nasledovné tvrdenia o parametroch citlivosti ceny opcie.
- Závislosť delty od času zostávajúceho do expirácie:

- Závislosť thety od ceny akcie:

- Závislosť delty od času zostávajúceho do expirácie:
Beáta Stehlíková (www)
Cvičenia z finančných derivátov, FMFI UK Bratislava, LS 2009/2010