Black-Scholesov vzorec, implikovaná volatilita, delta opcie
:: Cena európskej call a put opcie ::
- Call opcia:
function [v]=call(S,E,r,sigma,tau) d1=(log(S/E)+(r+0.5*sigma^2)*tau)/(sigma*sqrt(tau)); d2=(log(S/E)+(r-0.5*sigma^2)*tau)/(sigma*sqrt(tau)); v=S*normcdf(d1)-E*exp(-r*tau)*normcdf(d2)
- Príklad:
Úroková miera je jedno percento. Aká je cena call opcie s expiračnou cenou 120 USD a s expiračným časom pol roka, ak dnešná cena akcie je 100 USD a volatilita akcie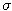 je 0.3?
je 0.3?
>> call(100,120,0.01,0.3,0.5) ans = 2.6056
- Put opcia: dá sa oceniť napríklad pomocou put-call parity:
- Uvažujme portfólio zložené z mínus jednej call opcie, jednej put opcie (na tú istú akciu, s rovnakou expiračnou cenou E a rovnakým expiračným časom) a jednej príslušnej akcie.
- V čase expirácie je hodnota portfólia E.
- Preto ak do expirácie zostáva čas
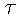 , hodnota portfólia je
, hodnota portfólia je 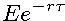 - cenu callu poznáme, takže môžeme vyjadriť cenu putu.
- cenu callu poznáme, takže môžeme vyjadriť cenu putu.
- Z linearity Black-Scholesovej rovnice vyplýva, že ak je koncová podmienka derivátu lineárnou kombináciou call a put opcií, rovnakou lineárnou kombináciou cien call a put opcií dostaneme cenu tohto derivátu.
:: Cvičenia (1) ::
- Vypočítajte cenu európskej call opcie s expiráciou o pol roka, ktorej expiračná cena je 50 USD. Dnešná cena akcie je 41 USD,
jej volatilita je 0.3. Úroková miera je pol percenta.
- Upravte funkciu call tak, aby ste mohli pracovať s vektorovými argumentmi a kresliť napríklad takého grafy:
S=0:0.1:100; plot(S,call(S,50,0.01,0.25,1));
Nakreslite graf s cenou akcie na x-ovej osi, na ktorom bude payoff call opcie a jej ceny pre niekoľko časov do expirácie.
Ukážka výstupu:.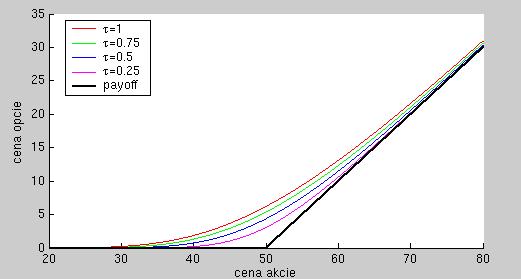
- Napíšte funkciu, ktorá počíta cenu putu. Vypočítajte cenu put opcie s expiračnou cenou 105 USD a s expiračným časom pol roka, ak dnešná cena akcie je 100 USD a volatilita akcie
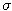 je 0.3.
je 0.3.
- Zostrojte stratégiu typu butterfly pre zvolené parametre. Znovu nakreslite graf
s cenou akcie na x-ovej osi, na ktorom bude payoff stratégie a jej ceny pre niekoľko časov do expirácie.
Ukážka výstupu pre nasledovné dáta: expiračné ceny 30, 40, 50 USD; volatilita akcie 0,25; úroková miera 0,01 (t.j. 1 percento).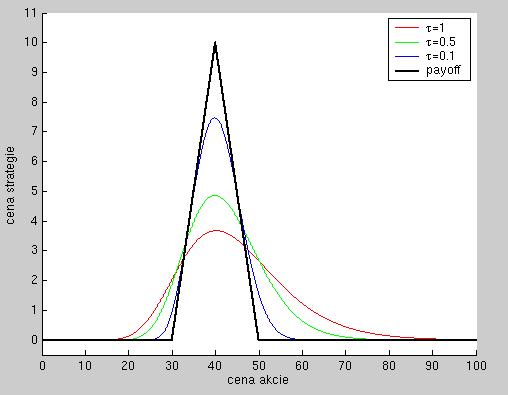
- Analýza reálnych cien opcií.
- V súbore ibm.txt si stiahnite denné dáta cien akcie firmy IBM a odhadnite z nich parameter
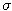 geometrického Brownovho pohybu - tzv. historickú volatilitu.
geometrického Brownovho pohybu - tzv. historickú volatilitu.
- Túto odhadnutú volatilitu budeme teraz dosadzovať do Black-Scholesovho vzorca.
Uvažujme nasledujúce dáta zo 7. marca 2011 pre ceny akcie a call opcií:
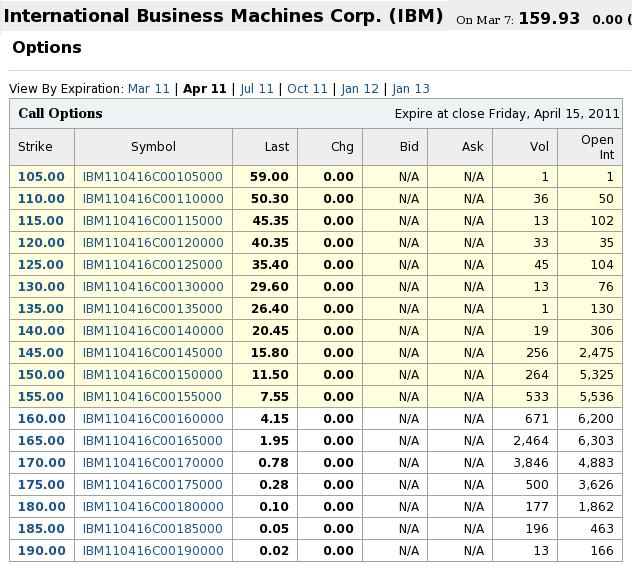
- Za bezrizikovú úrokovú mieru zoberieme výnos 3-mesačných Treasury bonds:
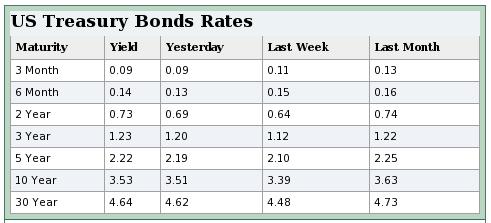
- Na výpočet času zostávajúceho do expirácie môžete využiť takýto výpočet (zohľadňuje soboty a nedele, prípadné sviatky treba odpočítať samostatne):
% pocet pracovnych dni medzi x,y vo formate 'mm/dd/yy' x=datenum('03/01/11'); y=datenum('03/31/11'); pocDni=0; for i=x+1:y den=weekday(i); % 1=nedela, 2=pondelok, ... if (den>1)&&(den<7) pocDni=pocDni+1; end; end; - Vypočítajte Black-Scholesove ceny týchto opcií a porovnajte ich s reálnymi trhovými cenami. Aké sú rozdiely v centoch? Aké sú relatívne rozdiely v percentách?
- V súbore ibm.txt si stiahnite denné dáta cien akcie firmy IBM a odhadnite z nich parameter
:: Implikovaná volatilita ::
- Implikovaná volatilita je taká hodnota volatility sigma, ktorej dosadením do Black-Scholesovho vzorca dostaneme trhovú cenu opcie.
- Závislosť ceny call opcie od volatility:
- Cena call opcie je rastúcou funkciou volatility.
- Ak volatilita konverguje k nule, limita ceny call opcie je max(0,S-E*exp(-r
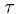 )).
)).
- Ak, naopak, volatlita ide do nekonečna, limita ceny opcie je aktuálna cena akcie S.
- Ak je teda trhová cena call opcie z intervalu (max(0,S-E*exp(-r
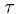 )),S), tak implikovaná volatilita existuje a je jednoznačne určená.
)),S), tak implikovaná volatilita existuje a je jednoznačne určená.
- Je viacero možností, ako implikovanú volatilitu prakticky vypočítať, tu je jedna z nich:
Definujeme funkciu rozdiel.m, ktorej parametrom je sigma a vracia rozdiel medzi skutočnou a Black-Scholesovou cenou. Ostatné parametre výpočtu sú definované ako globálne premenné:Príklad použitia: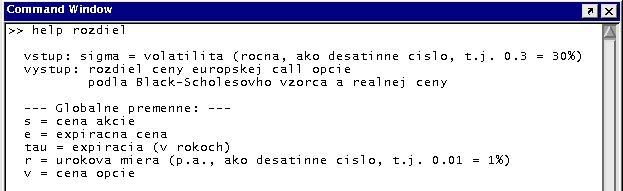
global s; global e; global tau; global r; global v; s=85.2; e=80; r=0.01; tau=0.5; v=11.12; % hladame nulovy bod tejto funkcie sig=0.01:0.01:0.5; plot(sig,rozdiel(sig),sig,zeros(1,length(sig))); fzero(@rozdiel,0.4);
Výstup:
:: Implikovaná volatilita ::
- Vyčítajte implikovanú volatilitu pre opcie na akcie IBM z cvičenia (1)/5. Zakreslite ich do grafu v závislosti od expiračnej ceny a pridajte do grafu historickú volatilitu.
Výstup: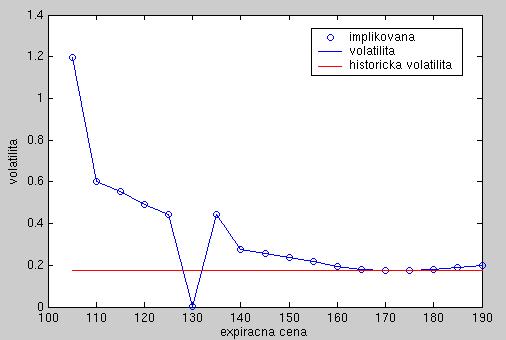
:: Závislosť ceny call opcie od ceny akcie ::
-
Na základe grafu môžeme vysloviť niekoľko hypotéz:
- V je rastúca funkcia S
- Ak S
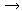 0, tak V
0, tak V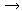 0.
0.
- Ak S
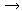
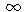 , tak sa cena opcie pribli?uje k payoff diagramu, takže by mohlo platiť
, tak sa cena opcie pribli?uje k payoff diagramu, takže by mohlo platiť
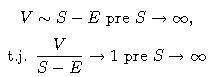
- Interpretácia:
- Ak sa cena akcie blíži k nule, znižuje sa pravdepodobnosť, že opciu uplatníme - opcia sa stáva bezcennou.
- Ak S
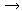
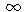 , tak
, tak
- Opcia sa zrejme bude realizovať, teda v čase expirácie dostaneme akciu a zaplatíme E, po odúročení tejto platby na súčasnú hodnotu vyslovíme hypotézu
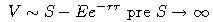
- Taká istá úvaha ako predtým, len dodáme, že pre S
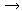
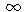 je E (aj súčasná hodnota) zanedbateľná, takže očakávame
je E (aj súčasná hodnota) zanedbateľná, takže očakávame
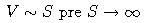
- Opcia sa zrejme bude realizovať, teda v čase expirácie dostaneme akciu a zaplatíme E, po odúročení tejto platby na súčasnú hodnotu vyslovíme hypotézu
- Ak je vyššia súčasná cena akcie, zvyšuje sa pravdepodobnosť, že ju uplatníme a dosiahneme zisk. Rovnako sa zvyšuje pravdepodobnosť vysokých cien akcie, a teda vysokého zisku z realizácie opcie.
- Matematicky:
- Vypočítame limitu V pre S
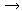 0 a ukážeme, že sa rovná 0.
0 a ukážeme, že sa rovná 0.
- Platia všetky tri navrhnuté aproximácie pre S
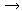
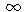 (vypočítame limity). Graficky sa presvedčíme, že sa líšia kvalitou aproximácie pre konečné hodnoty S.
(vypočítame limity). Graficky sa presvedčíme, že sa líšia kvalitou aproximácie pre konečné hodnoty S.
- Derivácia V podľa S je N(d1), čo je vždy kladné číslo. Teda V je rastúcou funkciou premennou S.
- Vypočítame limitu V pre S
:: Delta opcie ::
- Derivácia ceny opcie podľa ceny akcie, ktorú sme počítali, má väčší význam, ako ukázať rastúcu závislosť. Pri odvodení Black-Scholesovho vzorca vystupuje ako počet akcií, ktoré kúpime pri hedžovaní jednej predanej opcie a nazýva sa delta opcie.
:: Cvičenia (3) ::
- Nakreslite graf závislosti delty call opcie od aktuálnej ceny akcie. Nakreslite do jedného grafu deltu pre rôzne časy do expirácie. V čom sa líšia?
- Na základe hedžovania predanej opcie vysvetlite priebeh grafu z predchádzajúcej úlohy - znamienko, monotónnosť, priebeh pre tau blízke nule.
:: ďalšie príklady na precvičenie ::
- Vypočítajte hodnotu stratégie, ktorá pozostáva z kúpy call opcie s nízkou expiračnou cenou a predaja call opcie s vyššou expiračnou cenou s tou istou dobou splatnosti. Výpočet ceny stratégie realizujte pre nasledovné dáta: cena akcie 55 USD, volatilita akcie 0.4, úrok jeden a pol percenta, expiračná doba 3 mesiace, expiračné ceny sú 50 a 60 USD.
- Uvažujme call opciu na s expiračnou cenou 15 USD, ak dnešná cena akcie je 9 USD. Pre ktoré z nasledujúcich cien opcie -- 2 USD, 5 USD, 7 USD, 10 USD, 15 USD -- existuje implikovaná volatilita? Pre ktorú z nich je implikovaná volatilita najvyššia? Ako sa dá táto otázka zodpovedať bez výpočtu všetkých implikovaných volatilít?
- Implikovaná volatilita pre put opcie: Pre aký interval cien put opcií existuje? Je v týchto prípadoch určená jednoznačne? Zrealizujte výpočet implikovanej volatility pre konkrétnu put opciu.
- Delta pre put opcie. Vypočítajte deltu put opcie.
Nakreslite graf jej závislosti od aktuálnej ceny akcie.
Vysvetlite priebeh tohto grafu - znamienko, monotónnosť, priebeh pre tau blízke nule.
- Dokážte nasledovné tvrdenie o delte call opcie:
Zdroj: Y.Kwok: Mathematical Methods for Financial Derivatives.

- V súbore msft.txt je vývoj cien akcie firmy MSFT a opcií na tieto akcie. Formát:
Zvoľte si deň a načítajte dáta o vývoji akcie počas tohto dňa. Zvoľte si opciu a načítajte dáta o vývoji ceny tejto opcie v danom dni. V súbore msft-call-apr-25.txt sú tieto hodnoty pre call opciu s expiračnou cenou 25 USD a expiráciou v apríli (bid cena akcie, ask cena akcie, bid cena opcie, ask cena opcie).

- Vypočítajte implikovanú volatilitu pre každú minútu. Budete potrebovať úrokovú mieru, dáta o úrokových mierach z 20. marca 2003 sú napr. na stránke http://www.federalreserve.gov/releases/h15/20030324/. Zobrazte priebeh implikovanej volatility.
- Vypočítajte pre každú minútu deltu opcie, pričom za volatilitu budete dosadzovať implikovanú volatilitu z danej minúty. Zobrazte priebeh delty.
Cvičenia z finančných derivátov, 2011
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/
