:: Implikovaná volatilita ::

• Implikovaná volatilita je taká hodnota volatility , ktorej dosadením do Black-Scholesovho vzorca dostaneme trhovú cenu opcie.
  
  
• Závislosť ceny call opcie od volatility:
  • Cena call opcie je rastúcou funkciou volatility.
  • Ak volatilita konverguje k nule, limita ceny call opcie je max(0,S-E*exp(-r)).
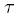  • Ak, naopak, volatlita ide do nekonečna, limita ceny opcie je aktuálna cena akcie S.
  • Ak je teda trhová cena call opcie z intervalu (max(0,S-E*exp(-r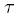)),S), tak implikovaná volatilita existuje a je jednoznačne určená.
  
  
• Je viacero možností, ako implikovanú volatilitu prakticky vypočítať, tu je jedna z nich:
  
  Čo sa tu počíta:
  
  
  
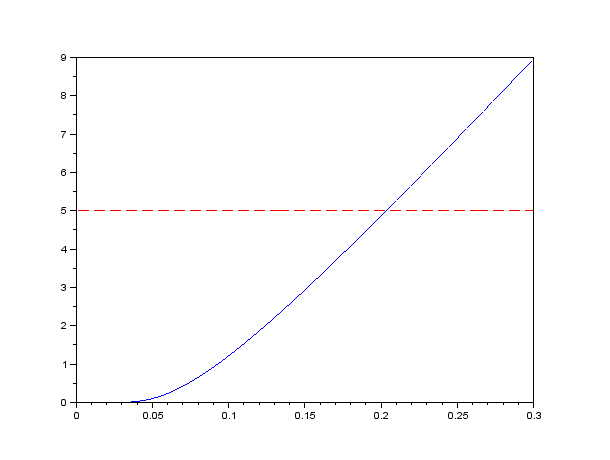
• Funkcia ImplVolCall v Scilabe je súčasťou kódu black_scholes.sci z predchádzajúceho cvičenia.

:: Cvičenia ::

1. Zväčšite rozsah volatility na x-ovej osi predchádzajúceho obázku tak, aby bolo vidieť jej limitu v nekonečne.
2. Zvoľte také sady parametrov, aby ste na grafe závislosti ceny opcie od volatility akcie videli obe možnosti, odkiaľ môže táto krivka začínať.
3. Vyskúšajte si samostatne výpočet implikovanej volatility pre zvolené parametre - toto je dôležité, tento výpočet budeme ešte potrebovať neskôr, na nasledujúcom cvičení "rozcvička" s takýmto zadaním za 2 body.
4. Implikovaná volatilita pre ostatné typy opcií - odvoďte, kedy existuje, naprogramujte funkciu na jej výpočet a použite ju na výpočet implikovanej volatility pre konkrétnu opciu:
   1. put opcia na akciu nevyplácajúcu dividendy
   2. call a put opcia na akciu vyplácajúcu dividendy so spojitou dividendovou mierou q

---