:: Implied volatility ::

• Implied volatility is the value of volatility which, after substituting into the Black-Scholes formula, gives the market value of the option.
  
  
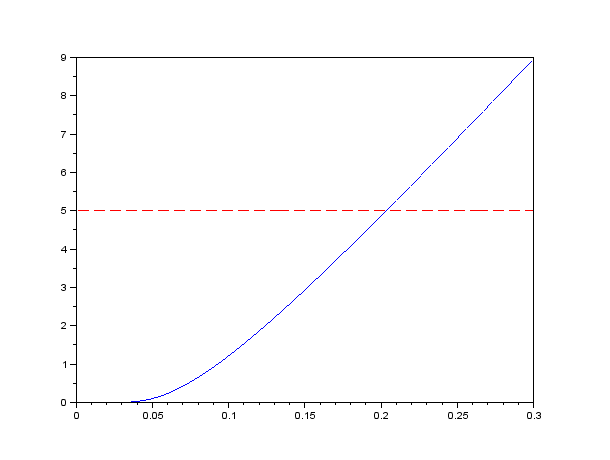
• Dependence of the call option price on the stock volatility:
  • The call option price is an increasing function of the volatility.
  • As the volatility approaches zero, the limit of the price is max(0,S-E*exp(-r)).
  • As the voltility approaches infinity, the option price approaches the stock value S
  • Hence, if the market price of an option is from the interval (max(0,S-E*exp(-r)),S), then the implied volatility exists and it is unique.
  
  
• There are several ways of implementing computation of implied volatility; here is one of them:
  
  What does it do:
  
  
  
• Scilab function ImplVolCall is a part of the file black_scholes.sci given with the previous topic.

:: Exercises ::

1. Modify the graph above - use a wider rage of volatility on the horizontal axis, so that the limit at infinity can be observed.
2. Choose the parameters values which show both possible beginnings of the curve (when stock price approaches zero).
3. Try the computation of the implied volatility for a given option - this is important; we will need it when studying so called Leland model.

:: Practice problems ::

1. Implied volatility for other options - derive its existence and uniqueness, write a script implementing its computation for the given data and use it to compute the implied volatility for selecte parameters:
   • put option written on a stock that does not pay dividends
   • call a put options on a stock that pays continuous dividends with continuous dividend rate q

---