Náhodné procesy, modelovanie cien akcií
:: Stochastický vývoj finančných veličín ::
-
Z priebehov cien akcií (ako aj iných finančných veličín - úrokových
mier, výmenných kurzov, ...) vidíme, že ich priebeh sa nedá popísať
deterministickou funkciou. Preto sa na ich modelovanie používajú náhodné
procesy.
-
Vľavo: trend (vývoj ceny akcie počas piatich rokov), vpravo: fluktuácie (vývoj ceny akcie počas niekoľkých hodín):
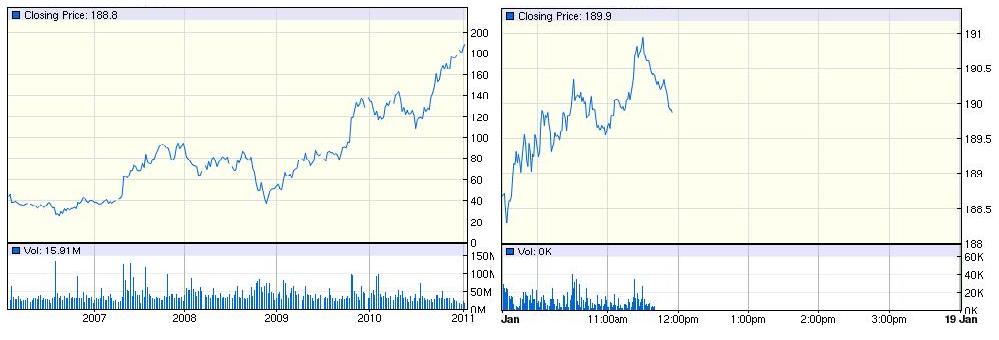 Zdroj: http://finance.google.com
Zdroj: http://finance.google.com
:: Wienerov proces a Brownov pohyb ::

| Stiahnite si [cv2procesy.sce] - súbor pre Scilab s doluuvedenými príkazmi, do ktorého budeme dopisovať ďalšie. |
-
Základným náhodným procesom, z ktorého sú ostatné odvodené, je Wienerov proces. Pripomeňme si jeho definíciu:
Náhodný proces {W(t), tĎalej bude w všade označovať Wienerov proces. 0} sa nazýva Wienerov proces, ak
0} sa nazýva Wienerov proces, ak
- prírastky
W(t+
 ) - W(t)
majú normálne rozdelenie s nulovou strednou hodnotou a s disperziou
) - W(t)
majú normálne rozdelenie s nulovou strednou hodnotou a s disperziou  ,
,
- pre každé delenie 0 = t0
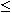 t1
t1 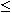 ...
... 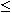 tn sú prírastky
Wti+1 - Wti nezávislé náhodné premenné s parametrami podľa predchádzajúceho bodu,
tn sú prírastky
Wti+1 - Wti nezávislé náhodné premenné s parametrami podľa predchádzajúceho bodu,
- W(0)=0,
- trajektórie sú spojité.
- prírastky
W(t+
-
Ako získame realizáciu Wienerovho procesu?
- Budeme generovať aproximáciu - hodnoty v diskrétnych bodoch typu (čas, hodnota), ktoré pospájame.
- Hodnoty budú v bodoch 0,
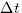 ,2
,2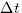 , . . ., kde
, . . ., kde 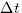 je dostatočne malý časový krok.
je dostatočne malý časový krok.
- Hodnota v čase 0 je 0.
- Prírastok na intervale [k
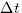 , (k + 1)
, (k + 1)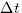 ] je náhodná premenná s nulovou strednou hodnotou
a varianciou
] je náhodná premenná s nulovou strednou hodnotou
a varianciou 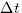 .
.
V Scilabe si najskôr definujeme pomocné funcie:

A teraz už môžeme nakresliť trajktóriu:

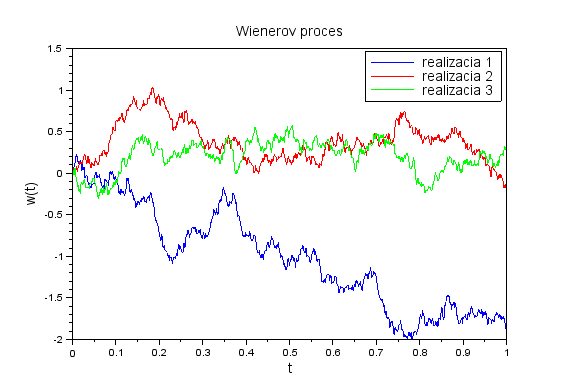
Nakreslite do jedného obrázku niekoľko trajektórií Wienerovho procesu. Ukážka výstupu:
-
Ak k násobku Wienerovho procesu pridáme lineárny trend:
dostávame proces, ktorý sa nazýva Brownov pohyb.
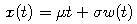
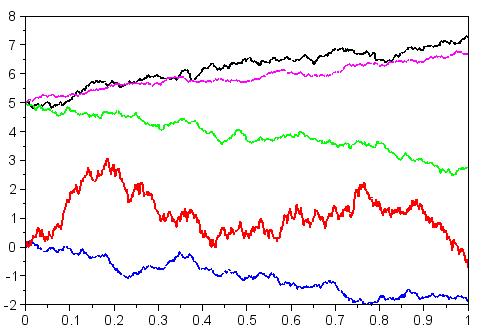
Ak je parameter
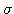 nulový, grafom je priamka. Pre nenulovú hodnotu
nulový, grafom je priamka. Pre nenulovú hodnotu 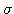 sa k tomuto lineárnemu trendu pridávajú náhodné fluktuácie.
sa k tomuto lineárnemu trendu pridávajú náhodné fluktuácie.
V Scilabe napríklad:

Nakreslite do jedného obrázku niekoľko trajektórií Brownovho pohybu, spolu s jeho strednou hodnotou. Ukážka výstupu:
:: Cvičenia (1) ::
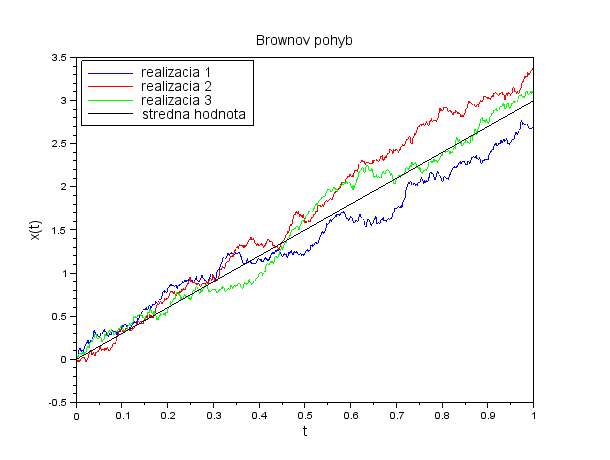
- Meňte parametre Brownovho pohybu a všímajte si, ako ovplyvňujú priebeh procesu. Potom priraďte procesy
- x1(t)=w(t)
- x2(t)=3*w(t)
- x3(t)=5+2*t+w(t)
- x4(t)=5+2*t+0.5*w(t)
- x5(t)=5-3*t+w(t)
:: Geometrický Brownov pohyb ::
-
Geometrický Brownov pohyb je proces definovaný vzťahom
pričom x0 predstavuje hodnotu procesu v čase 0.
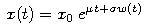
- Pricíp generovania v Scilabe:
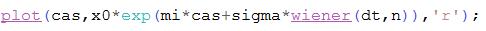
-
Ukážka trajektórií geometrického Brownovho pohybu:
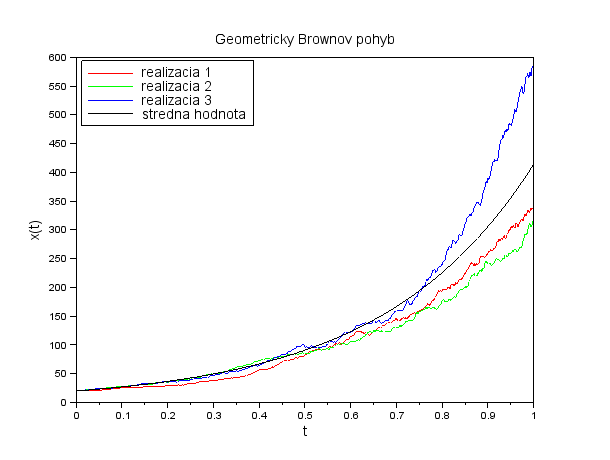
- Opakovanie z prednášky: Čomu sa rovná stredná hodnota geometrického Brownovho pohybu?
- Vytvorte podobný graf - s priebehmi realizácií a strednou hodnotou procesu.
:: Modelovanie cien akcií pomocou geometrického Brownovho pohybu ::
-
Cenu akcie S modelujeme geometrickým Brownovym pohybom:
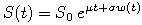
-
Ak sa cena akcie S riadi geometrickým Brownovym pohybom, tak pre výnosy dostávame
teda výnosy sú nezávislé náhodné premenné s normálnym rozdelením a uvedenými parametrami.
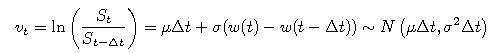
:: Cvičenia (2) ::
Pripomeňme si z prenášok z pravdepodobnosti definíciu a základné vlastnosti lognormálneho rozdelenia:- Náhodná premenná X má lognormálne rozdelenie, ak jej logaritmus ln(X) má normálne rozdelenie
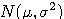 .
.
- Hustota náhodnej premennej X s lognormálnym rozdelením je
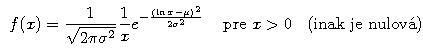
- Stredná hodnota a disperzia náhodnej premennej X s lognormálnym rozdelením je
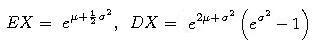

| Stiahnite si [cv2akcie.sce] - súbor pre Scilab s postupom riešenia nasledujúcich úloh a niektorými užitočnými funkciami. |
Predpokladajme, že cena akcie sa riadi geometrickým Brownovym pohybom s parametrami
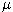 = 0.30,
= 0.30,
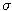 = 0.25
a že dnešná cena akcie je 150 USD.
= 0.25
a že dnešná cena akcie je 150 USD.
- Nakreslite hustotu rozdelenia ceny akcie o mesiac. Ako kontrolu porovnajte s histogramom vygenerovaných hodnôt ceny akcie v tomto čase.
- Aká je pravdepodobnosť, že o mesiac bude cena akcie menšia ako 140 USD?
- Aká je stredná hodnota štvrťročného výnosu? Aká je pravdepodobnosť, že bude záporný?
:: Odhadovanie parametrov GBP z cien akcií ::
| Stiahnite si [cv2data.sce] - súbor pre Scilab s doluuvedenými príkazmi a postupom. |
Ako získať parametre geometrického Brownovho pohybu z dát - odhadom parametrov normálneho rozdelenia z výnosov:
- Zopakujeme výpočet z prednášky. Použijeme dáta amzn.txt. Na začiatku súboru sú najstaršie dáta.
- Stiahneme si dáta.
- Nastavíme pracovný adresár tak, aby obsahoval súbor s dátami:
- Načítame dáta do Scilabu pomocou funkcie fscanfMat, ktorá má ako argument názov súboru uvedený v úvodzovkách.
- Definujeme časový krok medzi dvoma pozorovania dt, vyjadrený v rokoch. Máme denné dáta, teda dt=1/252:

- Definujeme výnosy - vytvoríme vektor výnosov v podľa horeuvedeného vzťhu.
- Vieme, že tieto výnosy majú normálne rozdelenie. Ďalej vieme,
že strednú hodnotu normálneho rozdelenia odhadujeme aritmetickým
priemerom a disperziu výberovou disperziou. Vypočítame teda priemer a
výberovú disperziu vektora v - budú to odhady veličín
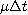 a
a 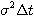

- Nakoniec vypočítame odhady samotných parametrov
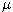 a
a 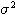 :
:

:: Odhad volatility interaktívne ::
- Na stránke https://bs81.shinyapps.io/sigma/
- Kvôli obmedzeniam na tzv. Active Hours bude aplikácia prístupná do 5.3.
:: Ďalšie príklady na precvičenie ::
- Označme tM čas, v ktorom trajektória Wienerovho procesu nadobúda svoje maximum na časovom intervale [0, 1]. Vygenerujte realizácie tejto náhodnej premennej a zobrazte jej histogram.
Na obrázku dolu je trajektória Wienerovho procesu a zodpovedajúca hodnota tM, spolu s ukážkou výsledného histogramu.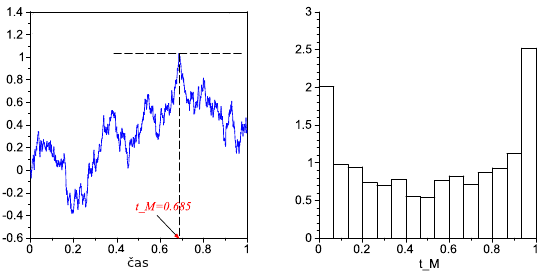
- Nech w je Wienerov proces, definujme
B(t) = w(t) - t w(1) pre čas t z intervalu [0, 1]. Tento proces je známy ako Brownov most (Brownian bridge). Nakreslite trajektórie tohoto procesu a vysvetlite jeho meno.
- Nech w je Wienerov proces, definujme proces
teda jeho hodnota v čase t je maximum Wienerovho procesu na intervale [0,t].
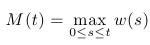
Na obrázku dolu je trajektória Wienerovho procesu a zodpovedajúca trajektória procesu M.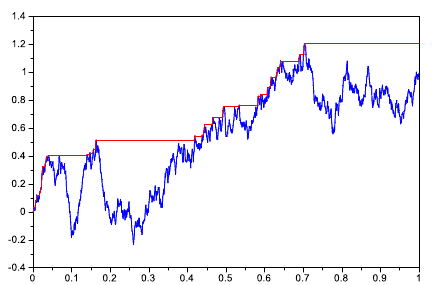
- Vygenerujte realizácie tohto náhodného procesu a zobrazte histogram jeho hodnôt v čase t=1.
- Odhadnite strednú hodnotu procesu v čase t=1. (Tu si treba uvedomiť, že pri výpočte maxima z hodnôt v diskrétnych časoch je maximum podhodnotené v porovnaní so skutočným maximom trajektórie. Preto na dosiahnutie dostatočnej presnosti odhadu strednej hodnoty nestačí generovať veľký počet simulácií, ale aj dostatočne jemné delenie časového intervalu.)
- Nech w je Wienerov proces, definujme proces m, ktorého hodnota v čase t je minimum Wienerovho procesu na intervale [0,t].
- Vygenerujte realizácie tohto náhodného procesu a zobrazte histogram jeho hodnôt v čase t=1.
- Odhadnite strednú hodnotu procesu v čase t=1. (Analogicky ako v predchádzajúcom príklade, treba si uvedomiť, že pri výpočte minima z hodnôt v diskrétnych časoch je minimum nadhodnotené v porovnaní so skutočným minimom trajektórie. Preto na dosiahnutie dostatočnej presnosti odhadu strednej hodnoty nestačí generovať veľký počet simulácií, ale aj dostatočne jemné delenie časového intervalu.)
Cvičenia z finančných derivátov, 2015
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://pc2.iam.fmph.uniba.sk/institute/stehlikova/