:: Typy súborov pre Scilab ::

• Doteraz nám stačilo definovať niekoľko málo funkcií a tie sme potom používali, pričom sme spúšťali len krátky kód.
• Teraz budeme mať viac funkcií - ceny call a put opcií (s dividendami aj bez), pre jednotlivé typy opcií implikovaná volatilita a faktory citlivosti.
• Scilab má dva typy súborov - do sci sa napíšu definície všetkých funkcií (a súbor ibsahuje len tieto definície), sce obsahuje samotný kód, pričom na začiatku sa nahrajú príkazom getd(); všetky funkcie definované v sci-súboroch v pracovnom adresári.
  
  
  
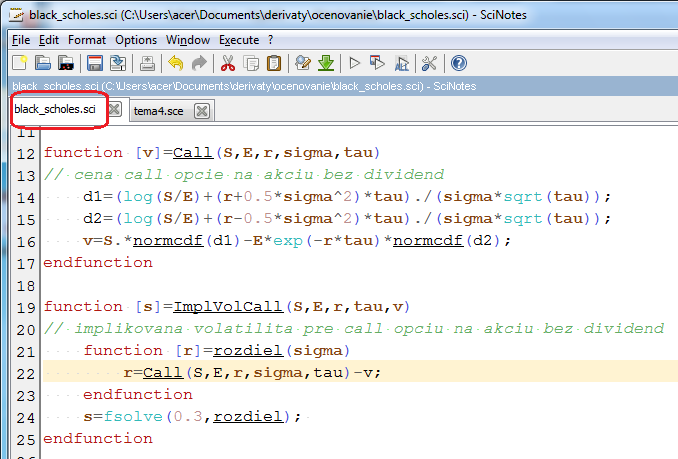
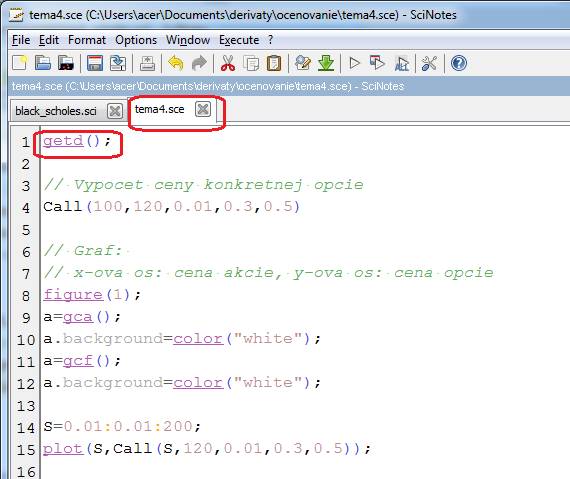
• Stiahnite si tieto súbory black_scholes.sci (tu sú definované funkcie na výpočet ceny call opcie na akciu bez dividend a implikovanej volatility pre takúto opciu) a tema4.sce

:: Cena európskej call a put opcie ::

• Príklad:
  Úroková miera je jedno percento. Aká je cena call opcie s expiračnou cenou 120 USD a s expiračným časom pol roka, ak dnešná cena akcie je 100 USD a volatilita akcie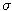 je 0.3?
  
  
  
• Put opcia: dá sa oceniť napríklad pomocou put-call parity:
  • Uvažujme portfólio zložené z mínus jednej call opcie, jednej put opcie (na tú istú akciu, s rovnakou expiračnou cenou E a rovnakým expiračným časom) a jednej príslušnej akcie.
  • V čase expirácie je hodnota portfólia E.
  • Preto ak do expirácie zostáva čas 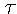, hodnota portfólia je 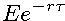- cenu callu poznáme, takže môžeme vyjadriť cenu putu.
  
  
• Z linearity Black-Scholesovej rovnice vyplýva, že ak je koncová podmienka derivátu lineárnou kombináciou call a put opcií, rovnakou lineárnou kombináciou cien call a put opcií dostaneme cenu tohto derivátu.

:: Cvičenia (1) ::

1. Vypočítajte cenu európskej call opcie s expiráciou o pol roka, ktorej expiračná cena je 50 USD. Dnešná cena akcie je 41 USD, jej volatilita je 0.3. Úroková miera je pol percenta.
   
   
2. Nakreslite graf s cenou akcie na x-ovej osi, na ktorom bude payoff call opcie a jej ceny pre niekoľko časov do expirácie.
   
   Ukážka výstupu:.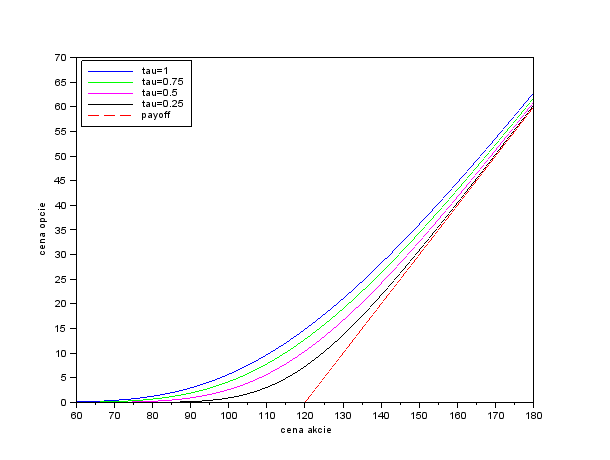
   
   
   
3. Napíšte funkciu, ktorá počíta cenu putu. Vypočítajte cenu put opcie s expiračnou cenou 105 USD a s expiračným časom pol roka, ak dnešná cena akcie je 100 USD a volatilita akcie 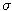je 0.3.
   
   
4. Zostrojte stratégiu typu butterfly pre zvolené parametre. Znovu nakreslite graf s cenou akcie na x-ovej osi, na ktorom bude payoff stratégie a jej ceny pre niekoľko časov do expirácie.
   
   Ukážka výstupu pre nasledovné dáta: expiračné ceny 120, 140, 160 USD; volatilita akcie 0,25; úroková miera 0,01 (t.j. 1 percento).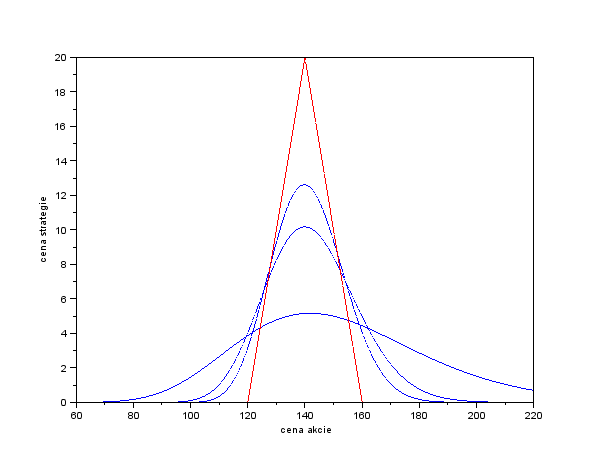
   

:: Implikovaná volatilita ::

• Implikovaná volatilita je taká hodnota volatility 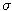, ktorej dosadením do Black-Scholesovho vzorca dostaneme trhovú cenu opcie.
  
  
• Závislosť ceny call opcie od volatility:
  • Cena call opcie je rastúcou funkciou volatility.
  • Ak volatilita konverguje k nule, limita ceny call opcie je max(0,S-E*exp(-r)).
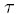  • Ak, naopak, volatlita ide do nekonečna, limita ceny opcie je aktuálna cena akcie S.
  • Ak je teda trhová cena call opcie z intervalu (max(0,S-E*exp(-r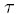)),S), tak implikovaná volatilita existuje a je jednoznačne určená.
  
  
• Je viacero možností, ako implikovanú volatilitu prakticky vypočítať, tu je jedna z nich:
  
  Čo sa tu počíta:
  

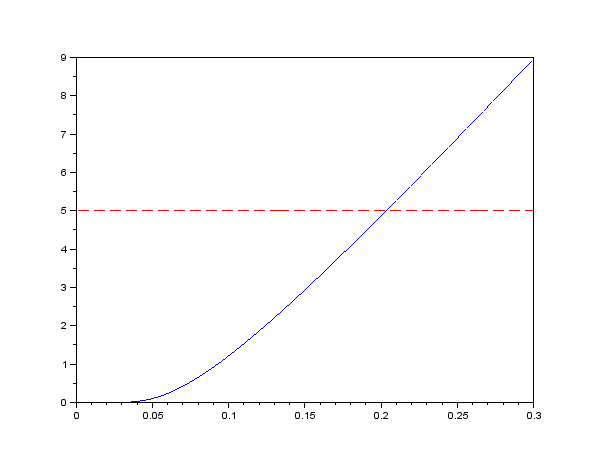
:: Implikovaná volatilita ::

1. Zväčšite rozsah volatility na x-ovej osi predchádzajúceho obázku tak, aby bolo vidieť jej limitu v nekonečne.
2. Zvoľte také sady parametrov, aby ste na grafe závislosti ceny opcie od volatility akcie videli obe možnosti, odkiaľ môže táto krivka začínať.
3. Vyskúšajte si samostatne výpočet implikovanej volatility pre zvolené parametre - toto je dôležité, tento výpočet budeme ešte potrebovať neskôr.

:: Delta opcie ::

• Derivácia ceny opcie podľa ceny akcie, rovná sa N(d₁)
• Pri odvodení Black-Scholesovho vzorca vystupuje ako počet akcií, ktoré kúpime pri hedžovaní jednej predanej opcie a nazýva sa delta opcie.
• Takémuto hedžovaniu opcií sa hovorí delta hedžing.

:: Cvičenia (3) ::

1. Koľko akcií musíme mať v portfóliu pri delta hedžingu, ak
   • sme vypísali 1000 call opcií s expiračnou cenou 25 USD a expiráciou o pol roka,
   • sme vypísali 1000 put opcií s expiračnou cenou 20 USD a expiráciou o štvrť roka,
   • sme kúpili 1000 call opciís expiračnou cenou 30 USD a expiráciou o rok,
   • sme kúpili 1000 put opcií s expiračnou cenou 20 USD a expiráciou o mesiac,
   ak dnešná cena akcie je 20 USD, volatilita je 0.3 a úroková miera je pol percenta?
   
   
2. Delta pre jednoduché deriváty.
   • Ako vyzerajú riešenia Black-Scholesovej PDR pre koncovú podmienku S a pre koncovú podmienku c (kde c je konštatna)? Čomu sa rovná ich delta a akú má tento výsledok interpretáciu?
   • Uvažujme Black-Scholesovu rovnicu na akciu s dividendami. Ako sa zmení riešenie PDR pre koncovú podmienku S a príslušná delta? Interpretujte finančne.
   
   
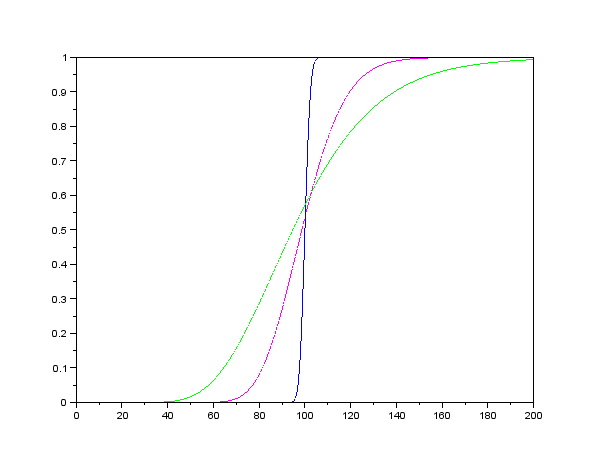
3. Na nasledujúcom obrázku sú zobrazené delty troch call opcií v závislosti od ceny akcie. Tieto opcie sa líšia expiráciou: o 1 deň, o pol roka, o 2 roky. Ostatné parametre sú rovnaké. Priraďte tieto expirácie grafom na obrázku.
   
   
   
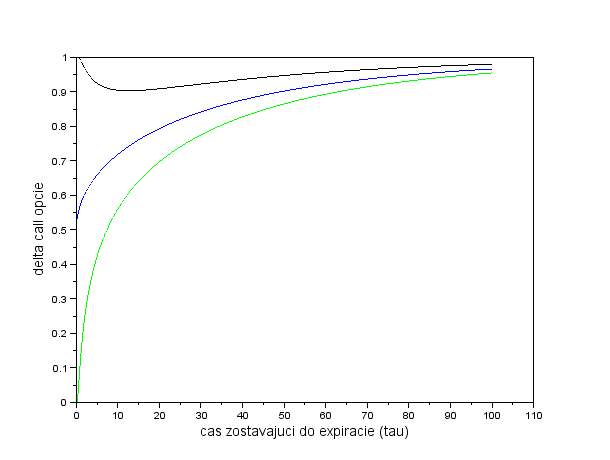
4. K čomu konverguje delta call opcie, ak čas zostávajúci o expirácie ide do nuly a ak ide do nekonečna? Od čoho to závisí? Na základe obrázka a interpretácie delty sformulujte hypotézu a dokážte ju.
   
   
   
   

:: Cvičenia (4) - ostatné parametre citlivosti ::

1. Z prednášky: závislosť delty od volatility, téma Black-Scholes III, posledný slajd:
   
   • Graficky znázornite závislosť delty od volatility pre rôzne opcie.
   • Explicitne vypočítajte DdeltaDvol, teda deriváciu delty podľa volatility akcie. Čo sa dá na základe vzorce očakávať pre opciu, ktorá je "deep in the money", ako sa spomína v článku? Porovnajte s numerickými výpočtami a grafmi.
   
   
2. Na quant.stackexchange.com sa objavila nasledovná otázka:
   
   Odpoveď začínala takto:
   
   • Vysvetlite, najskôr bez výpočtu konrétnych numerických hodnôt, prečo kontrapríklad hľadať ako ITM opciu na akciu s vysokou volatilitou.
   • Potom nájdite konkrétne hodnoty parametrov, ktoré budú tvoriť kontrapríklad k tvrdeniu z otázky.
   
   Diskusia pokračovala:
   
   • Ako závisí cena a delta opcie od ostatných parametrov? Nájdite hodnoty parametrov, ktoré budú tvoriť kontrapríklad pri volatilite 0.3 a pre opciu, ktorá nie je až tak výrazne ITM.

:: Ďalšie príklady na precvičenie ::

1. Vypočítajte hodnotu stratégie, ktorá pozostáva z kúpy call opcie s nízkou expiračnou cenou a predaja call opcie s vyššou expiračnou cenou s tou istou dobou splatnosti. Výpočet ceny stratégie realizujte pre nasledovné dáta: cena akcie 55 USD, volatilita akcie 0.4, úrok jeden a pol percenta, expiračná doba 3 mesiace, expiračné ceny sú 50 a 60 USD.
   
   
2. Príklad zo skúšky v zimnom semestri:
   
   
   
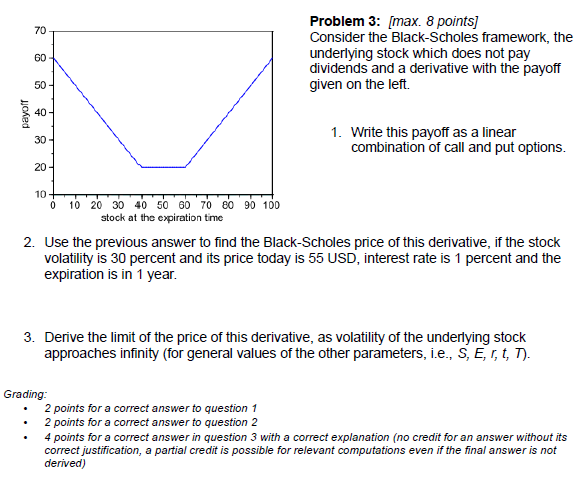
3. Uvažujme call opciu na s expiračnou cenou 15 USD, ak dnešná cena akcie je 9 USD. Pre ktoré z nasledujúcich cien opcie -- 2 USD, 5 USD, 7 USD, 10 USD, 15 USD -- existuje implikovaná volatilita? Pre ktorú z nich je implikovaná volatilita najvyššia? Ako sa dá táto otázka zodpovedať bez výpočtu všetkých implikovaných volatilít?
   
   
4. Implikovaná volatilita pre put opcie: Pre aký interval cien put opcií existuje? Je v týchto prípadoch určená jednoznačne? Zrealizujte výpočet implikovanej volatility pre konkrétnu put opciu.
   
   
5. Delta pre put opcie. Vypočítajte deltu put opcie. Nakreslite graf jej závislosti od aktuálnej ceny akcie. Vysvetlite priebeh tohto grafu - znamienko, monotónnosť, priebeh pre tau blízke nule.
   
   
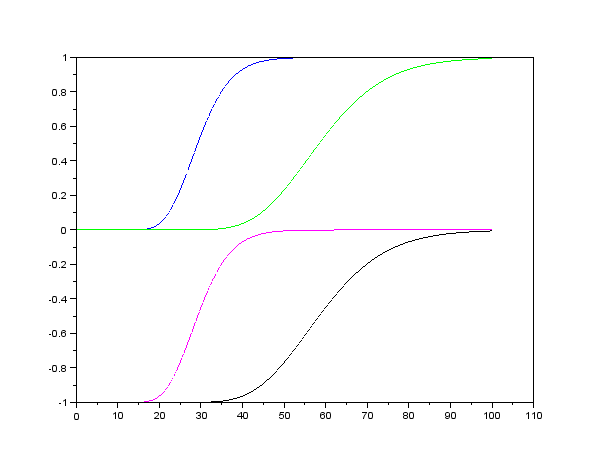
6. Na nasledujúcom obrázku sú zobrazené delty štyroch call opcií v závislosti od ceny akcie: call opcia s E=30, put opcia s E=30, call opcia s E=60, put opcia s E=60. Ostatné parametre sú rovnaké. Priraďte opcie grafom na obrázku.
   
   
   
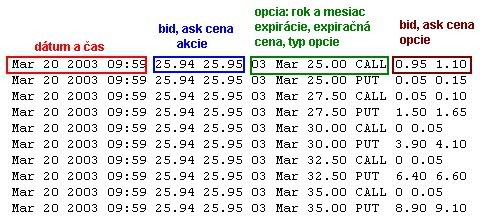
7. V súbore msft.txt je vývoj cien akcie firmy MSFT a opcií na tieto akcie. Formát:
   
   Zvoľte si deň a načítajte dáta o vývoji akcie počas tohto dňa. Zvoľte si opciu a načítajte dáta o vývoji ceny tejto opcie v danom dni. V súbore msft-call-apr-25.txt sú tieto hodnoty pre call opciu s expiračnou cenou 25 USD a expiráciou v apríli (bid cena akcie, ask cena akcie, bid cena opcie, ask cena opcie).
   • Vypočítajte implikovanú volatilitu pre každú minútu. Budete potrebovať úrokovú mieru, dáta o úrokových mierach z 20. marca 2003 sú napr. na stránke http://www.federalreserve.gov/releases/h15/20030324/. Zobrazte priebeh implikovanej volatility.
   • Vypočítajte pre každú minútu deltu opcie, pričom za volatilitu budete dosadzovať implikovanú volatilitu z danej minúty. Zobrazte priebeh delty.

---

---