Shiny applications for Vasicek model
:: Parameters of the Vasicek model ::
Unless stated otherwise, we consider the parameters from the paper (Episcopos, 2000), see Exercise 3 for the parameterization of the model in this paper.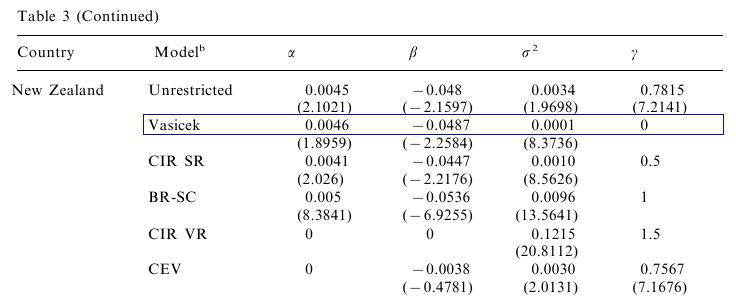
:: Shiny application (1): Term structures ::
- Preliminary exercise: Write a function white returns the interest rate as a function of the short rate r, time to maturity tau and market price of risk lambda. (The remaining parameters kappa, theta, sigma can be either imput parameters as well or global variables.
Plot several term structures for a selected value of market price of risk, which correspond to different values of the short rate.
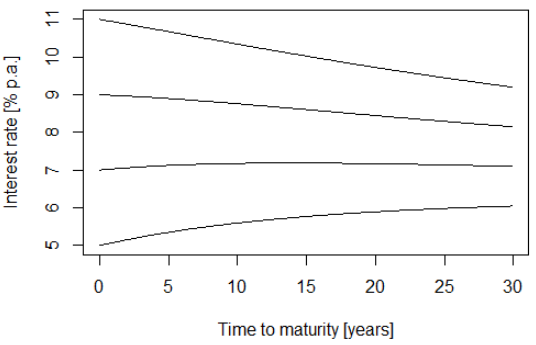
- Application: Create a shiny application which makes a similar plot for a selected value of market price of risk and range of x-variable (time to maturity). The user can check which term structures should be displayed (a set of possible short rate levels is given). Add the limit of the term structures (common to all the curves) to the plot.
Sketch of the application: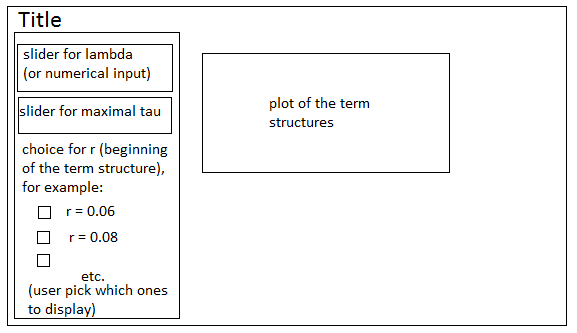
- Question from an old exam: Consider the parameters for the short rate given at the beginning. Find the value of the market price of risk, for which the limit of term structures is 1.2 times higher than the long-term limit of the short rate.
:: Shiny application (2): Fitting market price of risk ::
The values of kappa, theta, sigma have been estimated from the short rate. Consider the following term structure, when the short rate is equal to 0.08:| maturity in years | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| interest rate | 0.08282 | 0.08452 | 0.08856 | 0.08980 | 0.09295 | 0.09419 | 0.09750 | 0.09309 | 0.09954 | 0.10331 |
- Create an application which displays the points on this term structure and the theoretical term structure based on user's choice of the parameter lambda.
Sketch of the application: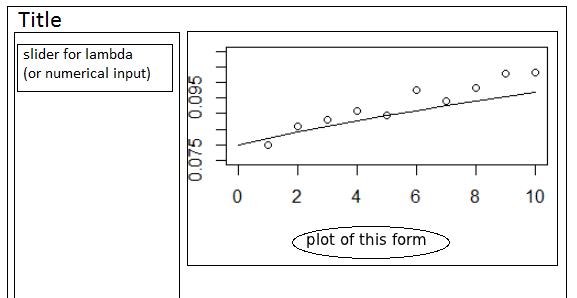
- Find an optimal lambda which minimizes the sum of squred differenced between theoretical and real interest rates.
:: Shiny application (3): Different shapes of term structures ::
- Recall from the lecture:
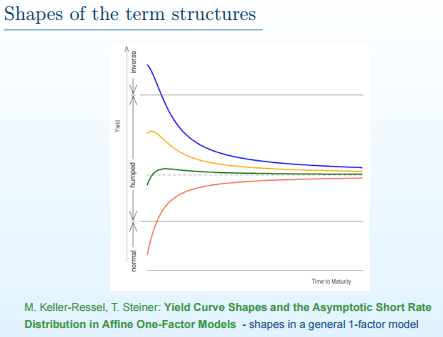
- Regions for the short rate which characterize the shape of the term structure can be found also in the original paper by O. Vasicek which uses the parametrization of the short rate in the form
The shape of the term structure is then given by the following:
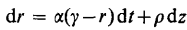 For example:
For example:
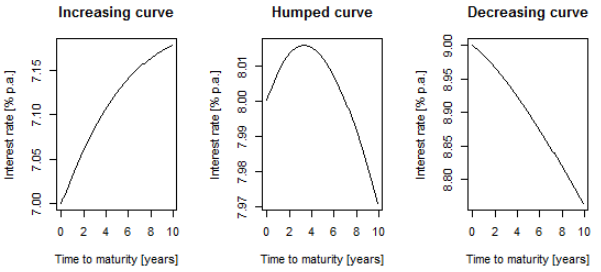
- Create an application in which the user selects a limit of the short rate. Application plots three terms structures, one for each shape.
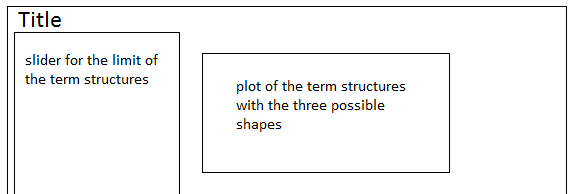
- How to choose the range for tau, so that the location of the hump is within this range? It can be shown that the point at which the maximum of the curve occurs, is the solution to the equation
where
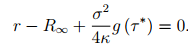
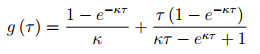
Financial derivatives - exercises
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://www.iam.fmph.uniba.sk/institute/stehlikova/
Beáta Stehlíková, FMFI UK Bratislava
E-mail: stehlikova@pc2.iam.fmph.uniba.sk
Web: http://www.iam.fmph.uniba.sk/institute/stehlikova/