Stochastický počet
:: Wienerov proces ::
- Opakovanie: Definujte Wienerov proces
- Stiahnite si súbor wiener.R, ktorý obsahuje okrem ďalších funkcií aj definíciu Wienerovho procesu:
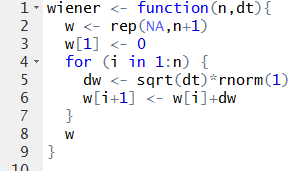
Poznamenajme, že výpočtovo to nemusí byť optimálne (cykly vo všeobecnosti nie sú) - môžete si to samostatne upraviť. Teraz budeme ale pracovať s touto funkciou. -
Môžeme vykresliť trajektóriu:

Dostaneme graf podobný tomuto:
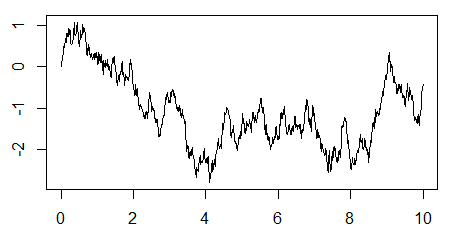
:: Cvičenia (1) ::
- Pridajte viac trajektórií do toho istého grafu:
Nie je isté, že nová trajektória sa zmestí do toho rozsahu y-ovej osi, ktorú náš graf (na základe prvej trajektórie) má. Vypočítajte hranice pre vertikálnu os, aby s pravdepodobnosťou 95 percent bol koncový bod trajektórie zobrazený na grafe.
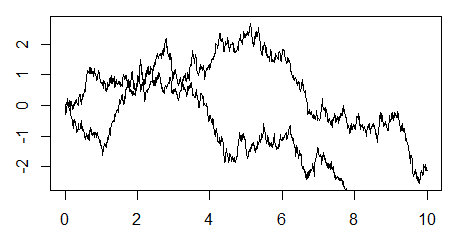
Samozrejme, to nezaručuje, že bude zobrazená celá trajektória. Maximum Wienerovho procesu sa budeme zaoberať v príkladoch na precvičenie.
- Vygenerujte hodnoty náhodnej premennej w(1)+w(2) (všimnime si, že nám stačí generovať Wienerov proces v časoch 1 a 2, jemné delenie nie je potrebné) a spravte histogram jej hodnôt. Vypočítajte pravdepodobnostné rozdelenie tejto náhodnej premennej a porovnajte so získaným histogramom.
:: Cvičenia (2) ::
Predpokladajme, že cena akcie sa riadi geometrickým Brownovym pohybom s parametrami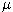 = 0.30,
= 0.30,
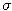 = 0.25
a že dnešná cena akcie je 150 USD.
= 0.25
a že dnešná cena akcie je 150 USD.
- Nakreslite hustotu rozdelenia ceny akcie o mesiac. Ako kontrolu porovnajte s histogramom vygenerovaných hodnôt ceny akcie v tomto čase.
- Aká je pravdepodobnosť, že o mesiac bude cena akcie menšia ako 140 USD?
- Aká je stredná hodnota štvrťročného výnosu? Aká je pravdepodobnosť, že bude záporný?
:: Odhadovanie parametrov GBP pre ceny akcií v R ::
- Budeme používať knižnicu quantmod, pomocou ktorej pohodlne stiahneme dáta o cenách akcií do R-ka:
Začiatok dát:


- Odhady budeme počítať z nasledovných cien:
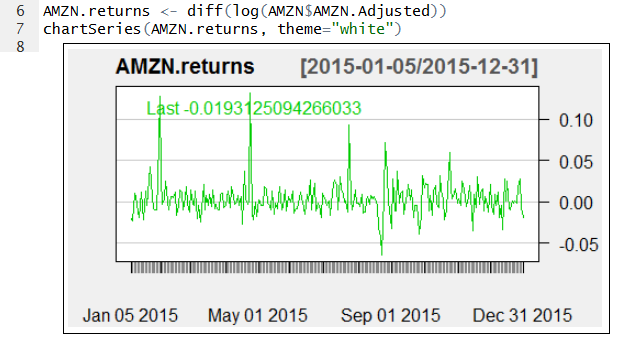
- Stiahnite si skript GBPakcie.R a odhadnite podľa postupu z prednášky parametre GBP, ktorým modelujeme cenu tejto akcie.
- Predpokladajme, že ceny dvoch akcií sú modelované dvoma GBP, pričom korelácia medzi prírastkami príslušných Wienerovych procesov je daná konštanta. Odvoďte koreláciu výnosov týchto akcií.
- Stiahnite si ceny dvoch akcií, odhadnite parametre GBP pre každú z nich a koreláciu Wienerovych procesov.
:: Viacrozmerná Itóova lema ::
Predpokladajme, že ceny dvoch akcií sú modelované dvoma GBP, pričom korelácia medzi prírastkami príslušných Wienerovych procesov je daná konštanta.- Odvoďte člen rádu dt pre súčin dS1 dS2 a vysletlite, prečo sú ostatné členy vyššieho rádu.
- Cena opcie V (napríklad spread option) závisí od ceny obidvoch opcií a od času. Vypočítajte diferenciál dV.
:: Ornstein-Uhlenbeckov proces ::
- Definícia: Ornstein-Uhlenbeckov proces je náhodný proces zadaný stochastickou diferenciálnou rovnicou
kde
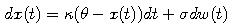
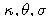 sú kladné konštanty. Takýto proces sa nazýva Ornstein-Uhlenbeckov proces.
sú kladné konštanty. Takýto proces sa nazýva Ornstein-Uhlenbeckov proces.
-
Príklad použitia na modelovanie úrokových mier je v príkladoch na precvičenie.
-
Najjednoduchším pôsobom, ako získať aproximáciu riešenia
stochastickej diferenciálnej rovnice je nahradiť diferenciály
diferenciami (analógia Eulerovej metódy pre obyčajné diferenciálne
rovnice, pri stochastických diferenciálnych rovniciach sa nazýva Euler-Marujamova metóda) - skript OUproces.R:
Ukážka:
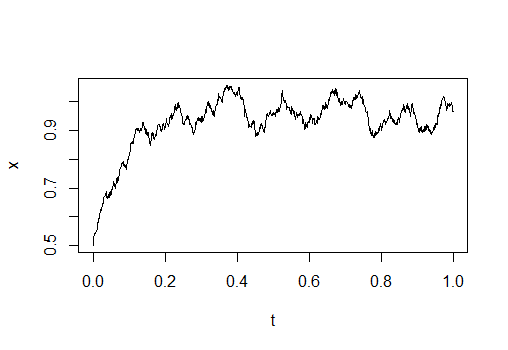
- Terminológia: Deterministická časť procesu (pri časovom diferenciáli dt) sa nazýva drift, stochastická časť (pri diferenciáli Wienerovho procesu dw) sa nazýva volatilita.
-
Priraďte nasledujúce hodnoty parametrov k ich trajektóriám:
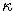 = 20,
= 20, 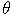 = 1,
= 1, 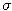 = 1
= 1
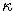 = 3,
= 3, 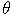 = 1,
= 1, 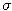 = 1
= 1
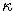 = 20,
= 20, 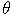 = 3,
= 3, 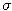 = 5
= 5
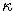 = 20,
= 20, 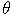 = 3,
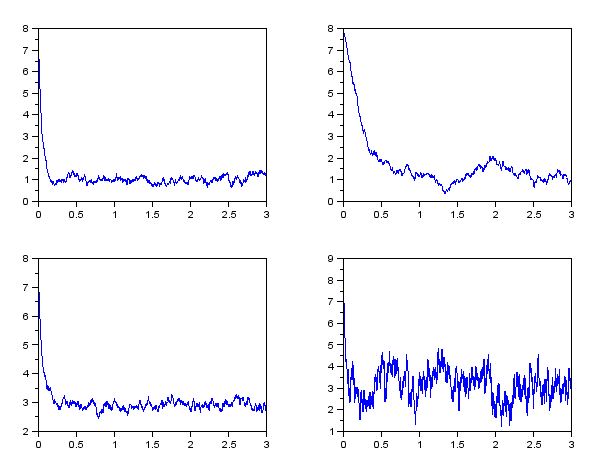
= 3, 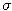 = 1
= 1
- Odvoďte - rovnakým postupom ako na prednáške pre geometrický Brownov pohyb - obyčajnú diferenciálnu rovnicu pre strednú hodnotu Ornstein-Uhlenbeckovho procesu a vyriešte ju.
:: Ďalšie príklady na precvičenie ::
- Označme tM čas, v ktorom trajektória Wienerovho procesu nadobúda svoje maximum na časovom intervale [0, 1]. Vygenerujte realizácie tejto náhodnej premennej a zobrazte jej histogram.
Na obrázku dolu je trajektória Wienerovho procesu a zodpovedajúca hodnota tM, spolu s ukážkou výsledného histogramu.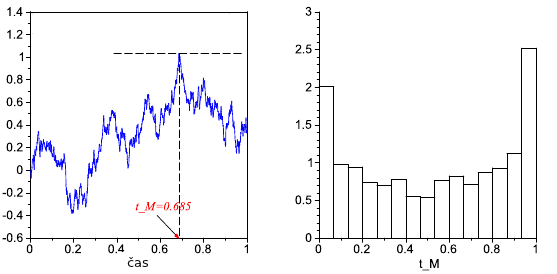
- Nech w je Wienerov proces, definujme
B(t) = w(t) - t w(1) pre čas t z intervalu [0, 1]. Tento proces je známy ako Brownov most (Brownian bridge). Nakreslite trajektórie tohoto procesu a vysvetlite jeho meno.
- Nech w je Wienerov proces, definujme proces
teda jeho hodnota v čase t je maximum Wienerovho procesu na intervale [0,t].
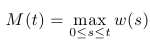
Na obrázku dolu je trajektória Wienerovho procesu a zodpovedajúca trajektória procesu M.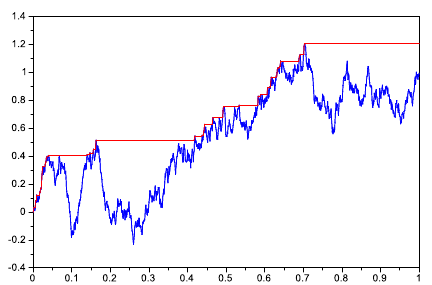
- Vygenerujte realizácie tohto náhodného procesu a zobrazte histogram jeho hodnôt v čase t=1.
- Odhadnite strednú hodnotu procesu v čase t=1. (Tu si treba uvedomiť, že pri výpočte maxima z hodnôt v diskrétnych časoch je maximum podhodnotené v porovnaní so skutočným maximom trajektórie. Preto na dosiahnutie dostatočnej presnosti odhadu strednej hodnoty nestačí generovať veľký počet simulácií, ale aj dostatočne jemné delenie časového intervalu.)
- Ornstein-Uhlenbeckov proces sa používa napríklad pri modelovaní úrokových mier. Vašíčkov model
predpokladá, že okamžitá úroková miera (prakticky - pri analýze
reálnych dát - úroková miera na krátky čas) sa riadi
Ornstein-Uhlenbeckovym procesom.
V článku Athanasios Episcopos: Further evidence on alternative continuous time models of the short-term interest rate. Journal of International Financial Markets, Institutions and Money 10 (2000) 199-212 autor odhadoval modely úrokových mier. Všeobecný model, ktorým sa zaoberal, jeŠpeciálnou voľbou niektorých parametrov dostávame konkrétne modely, jedným z nich je aj Vašíčkov model. Výsledky pre Nový Zéland (odhady parametrov pre mesačné dáta od apríla 1986 do apríla 1998 sú v nasledujúcej tabuľke: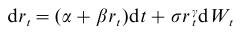 Zdroj: (Episcopos, 2000)
Zdroj: (Episcopos, 2000)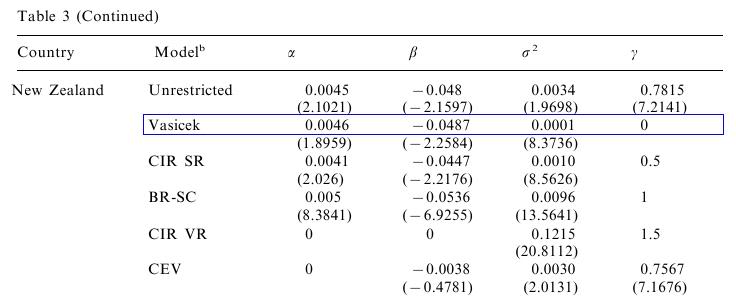
- Proces je v inom tvare, ako sme definovali Ornstein-Uhlenbeckov proces. Vyjadrite ho pomocou parametrov
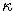 ,
, 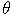 ,
, 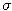 . K akej hodnote sa dlhodobo približuje úroková miera?
. K akej hodnote sa dlhodobo približuje úroková miera?
- Vygenerujte priebeh vývoja úrokovej miery na základe odhadnutých parametrov Vašíčkovho modelu. Zakreslite do jedného grafu niekoľko možných priebehov štartujúcich z rovnakej začiatočnej hodnoty, spolu so strednou hodnotou.
- Proces je v inom tvare, ako sme definovali Ornstein-Uhlenbeckov proces. Vyjadrite ho pomocou parametrov
- V článku Babbs, S. H., Nowman, K. B. (1999). Kalman filtering of generalized
Vasicek term structure models. Journal of Financial and Quantitative Analysis 34 (01),
115-130 sa navrhuje nasledovný model pre úrokovú mieru:
Vysvetlite tvrdenie "whose impact dies away exponentially" pomocou výpočtu strednej hodnoty faktora.

- V článku Schwartz, E. S. (1997). The stochastic behavior of commodity prices: Implications
for valuation and hedging. The Journal of Finance, 52(3), 923-973 autor navrhuje niekoľko modelov pre ceny komodít, jeden z nich je nasledovný:
Odvoďte, že z rovnice (1) vyplýva, že pre logaritmus ceny platia vzťahy (2), (3).

Poznámka: Toto bol jeden z modelov pre ceny komodít, ktorými sa zaoberal Miloslav Torda vo svojej bakalárskej práci Stochastické diferenciálne rovnice a ich aplikácie vo finančnom modelovaní z roku 2015. Modelmi pre ceny komodít sa v tomto kurze zaoberať nebudeme, pre záujemcov odkaz na bakalárku: [pdf]