:: Black Scholesova cena európskych opcií ::

• Stiahnite si black_scholes.R - R skript pre toto cvičenie.
  
  
• Máme tu funkciu, ktorá počíta Black-Scholesovu cenu call opcie na akciu, ktorá nevypláca dividendy:
  
• Teraz môžeme počítať napríklad:
  

:: Cvičenia (1) ::

1. Vypočítajte cenu európskej call opcie s expiráciou o rok, ak jej expiračná cena je 50 USD, súčasná cena akcie je 41 USA a jej volatilita je 0.3. Úroková miera je 0.5 percenta.
   
   
2. Nakrelite graf, ktorý má na x-ovej osi cenu akcie a zobrazuje ceny call opcie pre niekoľko rôznych časov do expirácie. Ukážka výstupu:.
   
   
   
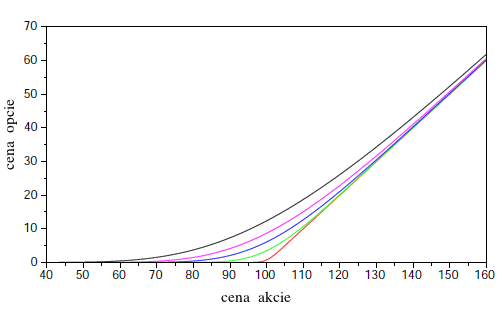
3. Napíšte funkciu, ktorá počíta Black-Scholesovu cenu put opcie. Potom vypočítajte cenu put opcie s expiračnou cenou 105 USD a expiráciou o pol roka, ak je aktuálna cena opcie 100 USD a jej volatilita je 0.3. Úroková miera je znovu 0.5 percenta.
   
   
4. Implementuje výpočet implikovanej volatility call opcie na akciu, ktorá nevypláca dividendy. Tento výpočet budeme potrebovať pri nelineárnom Lelandovom modeli, ktorý berie do úvahy transakčné náklady.



5. Predpokladajme, že akcia vypláca dividendy so spojitou dividendovou mierou q. Ako sa v tomto prípade zmení put-call parita? Ako sa potom dá vyjadriť cena put opcie pomocou ceny call opcie?
6. Na prednáške sme odvodili, že cena chooser opcie sa dá ľahko vypočítať, ak vieme oceniť call a put opcie. Napíšte funkciu, ktorá oceňuje takúto opciu v Black-Scholesovom modeli.

:: Závislosť ceny opcie od parametrov ::

Budeme pracovať s akciou bez dividend.

• Závislosť ceny call opcie od expiračnej ceny
  • Zobrazte závislosť ceny call opcie od expiračnej ceny graficky - pre zvolené hodnoty ostatných parametrov bude na x-ovej osi expiračná cena a na y-ovej cena call opcie.
  • V prvom týždni sme sa zaoberali vlastnosťami opcií, ktoré nezávisia od modelu pre cenu akcie - pre call opciu máme, že závislosť od expiračnej ceny musí byť nerastúca a konvexná.
  • Vypočítajte deriváciu Black-Scholesovej ceny call opcie podľa expiračnej ceny a pomocou lemy zo slajdov (strana 42) výraz pre deriváciu zjednodušte.
  • Ukážte, že táto derivácia je záporná a že je rastúcou funkciou expiračnej ceny. Z toho vyplýva, že závislosť Black-Scholesovej ceny call opcie od expiračnej ceny je klesajúca a rýdzo konvexná.
• Závislosť ceny chooser opcie od času voľby
  • Zobrazte závislosť ceny chooser opcie od času voľby. Prečo je takýto priebeh logický?
  • Vypočítajte deriváciu ceny chooser opcie podľa času voľby a určte jej znamienko.
  • Fixujte čas voľby a zobrazte závislosť ceny opcie od expiračnej ceny. Prečo je takýto priebeh logický? Numericky nájdite expiračnú cenu, pri ktorej je hodnota opcie minimálna.

:: Delta opcie a delta hedžing ::

• Derivácia ceny opcie podľa ceny akcie
• Pre call opciu na akciu, ktorá nevypláca dividendy, sa delta rovná N(d₁).
• V odvodení Black-Scholesovho vzorca je to počet akcií, ktoré musíme mať v portfóliu na jednu vypísanú opciu - takémuto zaisteniu portfólia sa hovorí delta hedging.

:: Cvičenia (2) ::

1. Koľko akcií musíme mať v portfóliu, ak sme
   • vypísali 1000 call opcií s expiračnou cenou 25 USD a expiráciou o pol roka,
   • vypísali 1000 put opcií s expiračnou cenou 20 USD a expiráciou o pol roka,
   • kúpili 1000 call opcií s expiračnou cenou 30 USD a expiráciou o pol roka,
   • kúpili 1000 put opcií s expiračnou cenou 20 USD a expiráciou o pol roka,
   pričom cena akcie dnes je 20 USD, jej volatilita je 0.3 a úroková miera je 0.5 percenta?
   
   
2. Nasledovný graf zobrazuje deltu troch call opcií ako funkcií ceny akcie. Tieto opcie majú rôzny čas do expirácie. 1 deň, 1/2 roka, 2 roky. Ostatné parametre sú rovnaké. Priraďte časy expirície ku grafom.
   
   
   
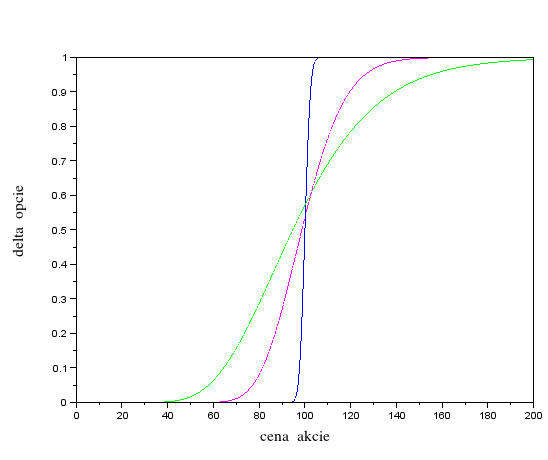
Aká je limita delty call opcie, ak čas do expirácie ide k nule a keď ide do nekonečna?




3. Predpokladajme, že akcia vypláca spojité dividendy. Čo očakávame pre deltu call opcie na základe jej interpretácie pomocou delta hedžingu? Aké bude mať znamienko a aká bude v porovnaní s deltou v prípade, že akcia dividendy nevypláca? Tieto vlastnosti dokážte.

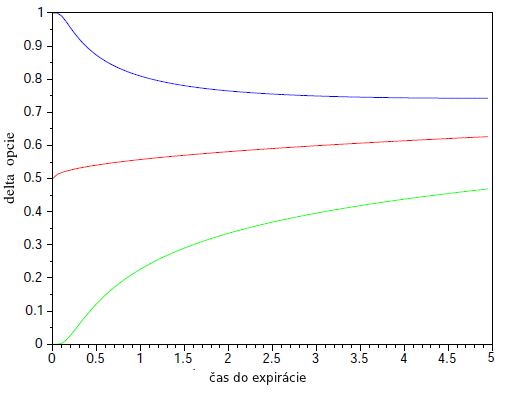
:: Príklady na precvičenie ::

1. Vypočítajte hodnotu stratégie, ktorá pozostáva z kúpy call opcie s nízkou expiračnou cenou a predaja call opcie s vyššou expiračnou cenou s tou istou dobou splatnosti. Výpočet ceny stratégie realizujte pre nasledovné dáta: cena akcie 55 USD, volatilita akcie 0.4, úrok jeden a pol percenta, expiračná doba 3 mesiace, expiračné ceny sú 50 a 60 USD.
   
   
2. Príklad zo skúškovej písomky:
   
   
   
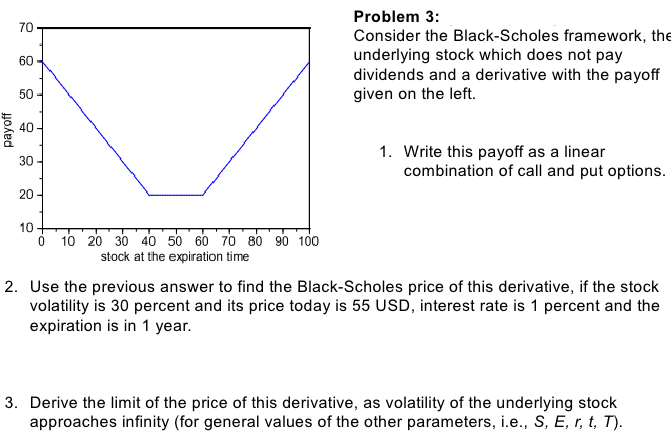
3. Príklad zo vzorovej skúškovej písomky:
   
   
   
4. Greeks pre binárnu "cash-or-nothing" opciu. Z prednášok poznáme cenu binárnej opcie.
   • Odvoďte jej deltu a vegu. Vysvetlite ich priebeh na základe finančnej interpretácie.
   • Pri akej cene akcie je delta maximálna? Odvoďte analyticky pre všeobecné hodnoty parametrov a skontrolujte svoj výpočet numerickou optimalizáciou pri zvolených parametroch.
   
   
5. Pre nasledovné deriváty zistite, ako ich zaisťovať pomocou delta hedžingu. Výpočet zrealizujte pre situáciu, v ktorej ste vypísali 1000 takýchto derivátov s expiráciou o mesiac, pričom aktuálna hodnota opcie je 200 USD, jej volatilita je 0.2 a úroková miera je 0.2 percenta:
   • Derivát, ktorý v čase expirácie vyplatí hodnotu 1000/S
   • Derivát, ktorý v čase expirácie vyplatí hodnotu S ln(S)
   
   
6. Delta pre jednoduché deriváty.
   • Ako vyzerajú riešenia Black-Scholesovej PDR pre koncovú podmienku S a pre koncovú podmienku c (kde c je konštatna)? Čomu sa rovná ich delta a akú má tento výsledok interpretáciu?
   • Uvažujme Black-Scholesovu rovnicu na akciu s dividendami. Ako sa zmení riešenie PDR pre koncovú podmienku S a príslušná delta? Interpretujte finančne.
   
   
7. Z prednášky: závislosť delty od volatility, posledný slajd:
   
   • Graficky znázornite závislosť delty od volatility pre rôzne opcie.
   • Explicitne vypočítajte DdeltaDvol, teda deriváciu delty podľa volatility akcie. Čo sa dá na základe vzorce očakávať pre opciu, ktorá je "deep in the money", ako sa spomína v článku? Porovnajte s numerickými výpočtami a grafmi.
   
   
8. Uvažujme opciu, ktorá vyplatí 1 USD, ak je v čase expirácie cena opcie medzi vopred zadanými hranicami E₁ and E₂ (inak je jej payoff nulový).
   • Vypočítajte Black-Scholesovu cenu tejto opcie. Návod: Použite vzťah pre cenu cash-or-nothing opcie z prednášky.
   • Vypočítajte deltu tejto opcie a nakreslite jej graf ako funkciu ceny akcie. Zopakujte pre niekoľko časov do expirácie? Čo sa deje, keď sa blížime k expirácii a prečo?


9. Na stránke quant.stackexchange.com nájdeme aj nasledovnú otázku:
   
   Odpoveď začína:
   
   • Vysvetlite, najskôr bez výpočtu konkrétnych numerických hodnôt, prečo by sme mali hľadať protipríklad medzi ITM opciami na akciu s veľkou volatilitou-
   • Následne, nájdite konkrétne hodnoty parametrov, aby ste dostali kontrapríklad k tvrdeniu z otázky.
   
   Diskusia pokračovala:
   
   • Aká je závislosť ceny a delty od ostatných paramerov? Nájdite hodnoty parametrov, pre ktoré dostaneme kontrapríklad pri volatilite rovnej 0.3 pre opciu, ktorá nie až tak výrazne ITM.

---

---